湖北桂花林场檫木次生林单木生长模型的研究

胡焕香 ，佘济云 ，李 俊 ，张 敏 ，孟 伟 ，程玉娜

（1中南林业科技大学，湖南 长沙 410004；2广东省林业调查规划院，广东 广州 510520）

湖北桂花林场檫木次生林单木生长模型的研究

胡焕香1，佘济云1，李 俊2，张 敏1，孟 伟1，程玉娜1

（1中南林业科技大学，湖南 长沙 410004；2广东省林业调查规划院，广东 广州 510520）

为了更好地开发和利用檫木资源并为其经营管理提供参考依据，利用大小比数并结合多模型选优法对湖北省国营桂花林场檫木次生林的单木直径生长过程进行了分析与探讨. 结果表明：不论是竞争优势木还是竞争劣势木，用Richards函数来拟合檫木的直径生长过程效果最好，其次是Schumacher函数，最差的是Gauss函数。但是Richards函数的参数偏多，并且通过Richards函数预估的直径生长量与檫木的实际生长状况不符合，因此，Schumacher函数是描述湖北桂花林场檫木次生林直径生长过程的最佳模型。

檫木次生林；生长模型；大小比数；直径

檫木Sassafras tzumu，别名檫树，为樟科檫木属落叶乔木，主要分布在长江以南地区，广泛作为用材林和风景林，其木材浅黄色，材质优良，细致，耐久，多用于水车、造船及上等家具；檫木春开黄花，且先花后叶，叶形奇特，秋季变红，花、叶均具有较高的观赏价值，多用于庭园、公园栽植或用作行道树、山区造林绿化，是行道绿化或城郊风景林的理想树种[1-2]。此外，檫木的根和树皮入药，具有活血散瘀、祛风去湿等功能。因此，系统、全面地研究檫木对于更加科学合理地开发、利用和保护这一树种具有重要意义。目前关于檫木的研究已有很多，但大多是关于生物量[3-5]、林分结构[6-7]、育苗与栽培[8-9]等方面的研究，对其单木生长模型[10]的研究还比较罕见。直径[11-12]是林分内部最重要、最基本的测树因子，其测量简单、方便而且精确，因此，本研究拟对湖北国营桂花林场的檫木次生林直径生长过程进行分析与探讨，以期为研究区檫木的经营管理提供一定的参考依据。

1 材料与方法

1.1 试验地概况

实验地点位于湖北省国营桂花林场，林场建于1964年，位于湘鄂赣边陲的湖北省崇阳县桂花泉镇，距离崇阳县城大约16 km。林场地处幕阜山北坡低山丘陵与江汉平原的过渡地带，属低山丘陵地貌[13]。整个林场森林覆盖面积约有1万hm2，活立木蓄积42万m3，是全国“十佳国有林场”，是鄂东南的森林氧吧，是崇阳县的一道绿色屏障。桂花林场属亚热带季风气候，气候温暖，四季分明，雨量充沛、湿热同步，年平均降雨量1 636.2 mm，年平均气温15.5℃。林场内土层深厚，土壤肥沃，十分适宜众多植物的生长与繁衍，生物多样性丰富。山上生长着大量的人工次生林，较常见的乔木树种有檫木、南酸枣Choerospondias axillaria、苦槠Castanopsis sclerophylla、杉木Cunninghamia lanceolata、 马 尾 松 Pinus massoniana、 枫 香Liquidambar formosana 等。

1.2 试验材料

2011年5月与7月，在湖北省国营桂花林场中选择具有代表性的檫木次生林林分类型，用罗盘仪分别设置6块面积大小为400 m2，规格为20 m×20 m的正方形标准地，对其中胸径≥5 cm的檫木进行每木检尺，用围尺测量胸径，用测高仪测量树高，并做好记录。依据标准地每木检尺数据，寻找2～3株与林分平均直径和平均高相接近（一般要求相差在±5%以下）且干形中等的林木作为平均标准木，每块标准地选取2棵标准木做树干解析。样地基本信息见表1。

表1 样地基本信息Table 1 Basic information of the sample plots

1.3 研究方法

1.3.1 林木竞争态势的研究方法

本研究利用大小比数[6,13]对檫木的竞争态势进行分类，从而科学、合理地表达现实林木的生长状态。大小比数是用来描述相邻木与参照木之间在胸径、树高、冠幅等某一指标上的个体优势程度，本研究定义为胸径大于参照木的相邻木占4株最近相邻木的株数比例，其计算公式如下：

式中：Ui表示大小比数； kij表示一个离散型的变量，当相邻木的胸径比参照木大时kij=1，反之kij=0。

1.3.2 单木生长模型的选择

以林分中各单株林木为基本单位，以与其相邻木之间的竞争关系为基础，模拟林分中单株树木生长过程的模型，称为单木生长模型[14]。用来描述单木生长的模型有很多，本研究根据实际情况来选取以下5个逻辑性强，适应性广的数学模型对湖北省国营桂花林场的檫木次生林的直径生长过程进行研究与分析。并利用DPS软件来处理与分析数据。

（1）Logistic函数：

（2）Gauss函数：

（3）Richards函数：

（4）Gompertz函数：

（5）Schumacher函数：

式中：y表示直径生长量；k、a、b、c为随机参数；t表示树木的年龄。

1.3.3 模型的求解与检验

本研究利用麦夸特法来求取各模型的参数，并通过方差分析来对模型的拟合效果进行显著性检验。在拟合过程中，可根据数据拟合图中实际观测值和拟合曲线的拟合情况、残差平方和、决定系数及显著水平的高低来选择最优的模型。残差平方和越小，决定系数越大，显著水平越低，参数越少，则拟合的效果越理想。

2 结果与分析

2.1 标准木竞争态势的划分

由于不同林分的生长条件不同，其竞争状态也存在差异，因此对同树种不同竞争态势的林木建立相应的生长模型是更加科学、合理的。依据大小比数可以将竞争态势分为两类，当大小比数≥0.5时，为竞争优势木，反之为竞争劣势木。经统计分析，湖北省国营桂花林场檫木次生林12株标准木的大小比数分布情况如图1所示。由图1可知，竞争优势木（大小比数≥0.5）与竞争劣势木（大小比数＜0.5）的标准木株树均为6株，说明檫木次生林的竞争态势比较均衡。

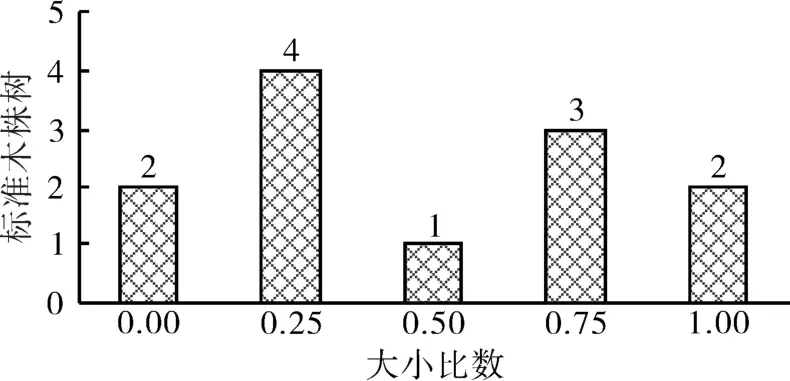
图1 檫木次生林12株标准木的大小比数分布Fig.1 Neighborhood comparison of 12 standard wood in S. tsumu secondary forest

2.2 单木生长模型的拟合与检验

由单木生长模型的拟合与检验结果见表2。可知，不论是竞争优势木还是竞争劣势木，5种数学模型对檫木次生林生长过程的拟合效果都比较接近，而且效果都非常理想，直径生长量与树木年龄回归关系均表现为极其显著。就单木（无论是竞争优势木还是竞争劣势木）而言，残差平方和最小，决定系数最大，对现有标准木数据拟合效果最好的都是Richards函数，其次是Schumacher函数，Gauss函数的拟合效果最差。残差平方和的大小顺序为：Richards函数＜Schumacher函数＜Gompertz函数＜Logistic函数＜Gauss函数；决定系数大小排序均为：Richards函数＞Schumacher函数＞Gompertz函数＞Logistic函数＞Gauss函数。说明Richards函数用来拟合湖北省国营桂花林场檫木次生林的单木生长过程效果最佳，其次是Schumacher函数，Gauss函数的拟合效果最差。

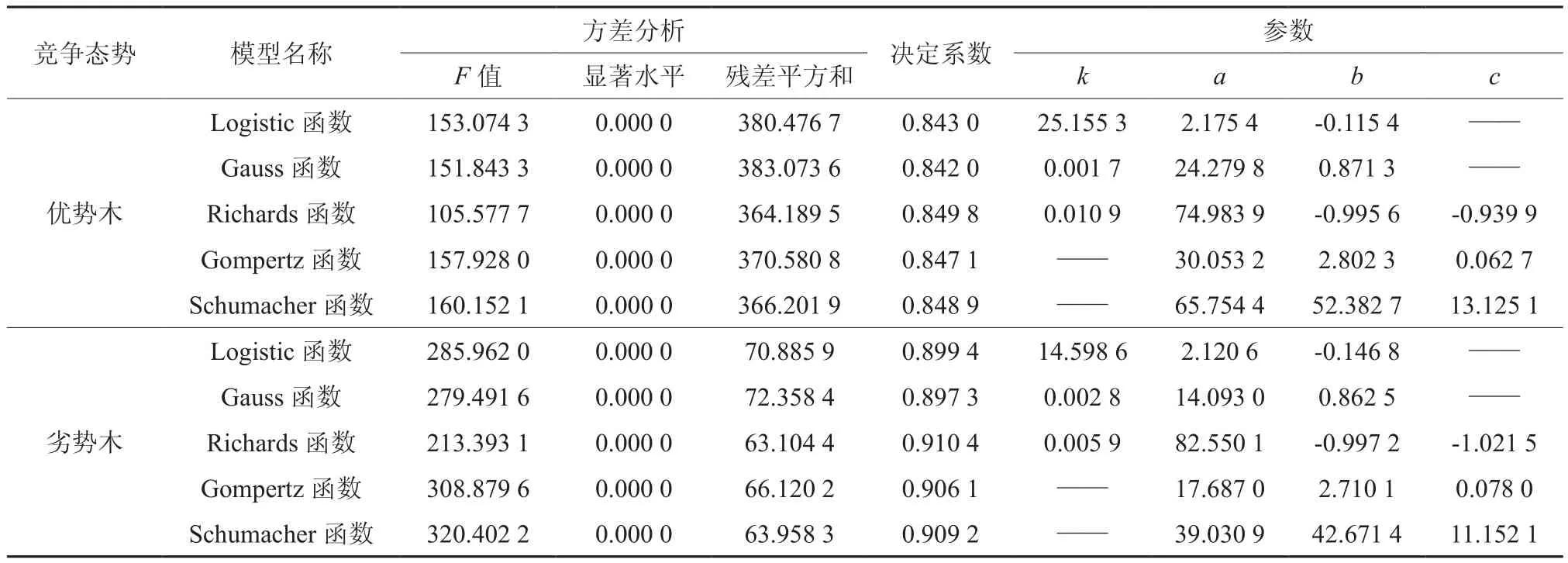
表2 单木生长模型的拟合与检验结果Table 2 Fitting and testing results of individual tree growth model

2.3 直径生长量预估分析

由直径生长量预估分析结果（见图2和图3）可知，从整体而言，无论是竞争优势木还是竞争劣势木，不论是直径总生长量还是直径连年生长量，5种数学模型对现有标准木数据的拟合效果都比较接近，并且重合度很高。在总生长量方面，竞争优势木基本上都是从40年左右开始明显分化，而竞争劣势木则是在30年左右开始明显分化，Richards函数预估的直径总生长量最大，Gauss函数预估的直径总生长量最小，其大小排序为：Richards函数＞Schumacher函数＞Gompertz函数＞Logistic函数＞Gauss函数。

在连年生长量方面，竞争优势木在5年左右出现第一个明显高峰，随后出现一个5年左右时间的缓慢生长期，之后生长速率一路上升至20年左右到达连年生长第二高峰，随后又开始进入缓慢生长期直至衰老；竞争劣势木在5年左右出现一个第1个明显的高峰，随后出现一个5年左右时间的短时期缓慢生长期，之后生长速率一路上升至15年左右到达连年生长第2个高峰，随后又开始进入缓慢生长期直至衰老。Gauss函数的收敛速度最快，Richards函数的收敛速度最慢，5中数学模型收敛速度的快慢排序为：Gauss函数＞Logistic函数＞Gompertz函数＞Schumacher函数＞Richards函数。

图2 竞争优势木直径生长量预估Fig. 2 Forecast amount of diameter growth of dominant tree

图3 竞争劣势木直径生长量预估Fig.3 Forecast amount of diameter growth of oppressed tree

就成熟期和生长停止期而言，在竞争优势木方面：Logistic函数、Gauss函数和Gompertz函数3种模型的成熟期和生长停止期都出现的较早，在20年左右出现成熟期，在55年左右出现生长停止期，与檫木次生林生长的现实状况不符合。Richards函数在5年左右到达高峰后一路缓慢走低，因此无法判断成熟期，5～100年一直为缓慢生长期，100年左右也未出现生长停止期；Schumacher函数的成熟期出现的比较适中，20年左右出现成熟期，而在20～100年出现缓慢生长期，与檫木次生林的现实生长状况比较符合。在竞争劣势木方面：Logistic函数、Gauss函数和Gompertz函数3种模型的成熟期和生长停止期都出现的较早，在15年左右出现成熟期，在50年左右出现生长停止期，不符合檫木次生林生长的实际状况。Richards函数在5年左右到达高峰后一路缓慢走低，因此无法判断成熟期，5～100年一直为缓慢生长期，100年左右也未出现生长停止期；Schumacher函数的成熟期出现的适中，15年左右出现成熟期，而在15～100年出现缓慢生长期，较符合檫木次生林的实际生长状况。

3 结论与讨论

本研究利用5个生长模型对湖北省国营桂花林场的檫木次生林的单木直径生长过程进行了拟合，得出对现有标准木数据拟合效果最好的是Richards函数，其次是Schumacher函数，而Gauss函数的拟合效果最差。但是考虑到Richards函数的参数较多（有4个参数），而拟合效果与其相近的Schumacher函数的参数适当偏少（有3个参数），从减少模型复杂程度方面考虑，选择Schumache函数作为檫木次生林的单木直径生长模型最为合适。此外，根据直径生长量预估分析的结果可知，无论是竞争优势木还是竞争劣势木，Richards函数都无法判断檫木直径生长过程的成熟期，而通过Schumache函数来判断成熟期得出的结果最为理想，与檫木次生林的实际生长情况十分吻合。因此，不论是竞争优势木还是竞争劣势木，Schumache函数均是描述檫木次生林直径生长过程的最理想模型，竞争优势木与竞争劣势木的直径生长模型表达式分别为：y=65.754 4exp[-52.382 7/ (13.125 1+t)]；y=39.030 9exp[-42.671 4/(11.152 1+t)]。

檫木是湖北省国营桂花林场的主要树种之一，研究结果可以用来直接判定檫木各单株木的直径生长状况和生长潜力，这对于研究区檫木林分的集约经营、生长与收获预估等方面具有一定的参考价值。但是由于条件限制，本研究所选取的样地和标准木数量偏少，这对研究结果会造成一定的影响。如果今后的研究能对这些方面加以补充和完善，并增加对树高、冠幅、断面积等因子进行单木生长模型探讨，研究成果将会更加具有应用与参考价值。

[1] 田大伦,张昌剑,罗中甫,等.天然擦木混交林的生物量及营养元素分布Ⅰ.生物生产量及生产力[J].中南林学院学报,1990, 10(2):121-127.

[2] 范海兰,洪 滔,吴承祯.檫木种群基面积增长规律研究[J].江西农业大学学报,2005，27(5)：744-747.

[3] 沈 燕，田大伦，闫文德，等.湖南沅陵天然次生白栎＋檫木＋杉木群落生物量及其分布规律[J].中南林业科技大学学报，2011，31 (5):44-50.

[4] 沈 燕，田大伦，项文化，等.天然次生檫木枫香混交林生物量及生产力研究[J].中南林业科技大学学报，2011,31(5):26-30.

[5] 张 琼，洪 伟，吴承祯，等.天然更新檫木林的能量分析[J].植物资源与环境学报，2004，13(2):36-39．

[6] 曾思齐，李东丽，宋武刚，等.檫木次生林空间结构的研究[J].中南林业科技大学学报，2012，32 (3):1-6．

[7] 李 俊.南方集体林区典型林分类型结构特征及生长模型研究[D].长沙：中南林业科技大学，2012．

[8] 黄宝祥，朱培林，符树根.檫木的组织培养[J].江西林业科技 , 2010，(4)：11-12．

[9] 丁小飞，陈红林，曹 健.檫木三个群体的遗传结构初探[J].湖北林业科技,2006，(5)：1-2．

[10] 刘 平,王玉涛,杨 帆.基于单木生长模型的森林动态模拟系统研究进展[J].世界林业研究,2011,24(5):25-29．

[11] 李 俊，佘济云，胡焕香，等.昌化江流域天然林直径结构研究[J].中南林业科技大学学报，2012,32 (3):37-43．

[12] 胡焕香，佘济云，刘立武，等.海南阿陀岭4种加勒比松林分直径分布规律研究[J].中国农学通报,2012,28(22):16-21.

[13] 曾思齐，李 俊，李东丽，等.南方集体林区南酸枣次生林林分结构研究[J].中南林业科技大学学报，2012,32 (4):1-6.

[14] 孟宪宇.测树学[M].北京：中国林业出版社，2008:254-293.

Study on individual tree growth model of Sassafras tsumu secondary forest on Osmanthus Forest Farm in Hubei Province

HU Huan-xiang1, SHE Ji-yun1, LI Jun2, ZHANG Min1, MENG Wei1, CHENG Yu-na1

(1.Central South University of Forestry and Technology, Changsha 410004, Hunan, China; 2.Forestry Surveying and Designing Institute of Guangdong Province, Guangzhou 510520, Guangdong, China)

In order to develop and use Sassafras albidum better and provide reference basis for its operation and management, the neighborhood comparison combined with multi-model selection methods were used to analyze and discuss individual tree diameter growth progress of S.tsumu secondary forest in Osmanthus forest farm in Hubei province. The results show that whether it is a dominant tree or oppressed tree,Richards function was the best to fit the growth process of S. albidum diameter, better than Schumacher function, while Gauss function’s fitting effect was the worst. However, the parameters of Richards function were too much, and the amount of diameter growth of S. albidum estimated by Richards function was not incompatible with the actual growth conditions. Therefore, Schumacher function was the best model to describe the diameter growth process of S. tsumu secondary forest in Osmanthus forest farm in Hubei province.

Sassafras tsumu secondary forest; growth model; neighborhood comparison; diameter; Hubei Province

S758.1

A

1673-923X(2013)04-0061-05

2012-12-03

国家林业局行业公益性项目“南方集体林区次生林抚育间伐与高效利用技术研究”（201004032）；湖南省“十一五”重点学科建设计划资助项目“森林经理学科”(2006-028-0015)

胡焕香（1985-），男，河南信阳人，硕士研究生，主要从事林业信息工程和森林可持续经营方面的研究

佘济云（1966-），男，湖南邵东人，博士，教授，博导，主要从事森林经理和林业资源管理方面的教学和科研工作；E-mail：shejiyun@126.com

[本文编校：吴 彬]