限定混合模型模拟不规则和多峰直径结构分布—— 以长白山云冷杉林为例

杜 志 ，亢新刚 ，岳 刚，徐 光 ，赵东宁 ，杨艺军 ，高 祥

(1. 北京林业大学 省部共建森林培育与保护教育部重点实验室，北京 100083；2.汪清林业局，吉林 汪清 133200)

限定混合模型模拟不规则和多峰直径结构分布
—— 以长白山云冷杉林为例

杜 志1，亢新刚1，岳 刚1，徐 光2，赵东宁2，杨艺军2，高 祥2

(1. 北京林业大学 省部共建森林培育与保护教育部重点实验室，北京 100083；2.汪清林业局，吉林 汪清 133200)

以长白山地区6块云冷杉林样地调查数据为基础，采用限定混合Weibull模型方法，并利用传统的负指数模型和Weibull模型作为参照，对直径分布进行了模拟。结果表明：样地直径分布呈多峰、rotated-sigmoid等不规则分布；数学统计表明限定混合Weibull模型的直径拟合效果最好，其次是Weibull模型，最后为负指数模型，尤其在模拟双峰和rotated-sigmoid分布时混合模型优势明显；残差图显示径阶大于28cm后，相对于其它两个模型，限定混合Weibull模型的残差值更接近于0。限定混合模型是一种较好的具有高灵活性和高精度的林分直径模拟方法。

云冷杉林；直径分布；限定混合Weibull模型；负指数模型；Weibull模型

直径分布是森林结构的重要组成部分[1-2]，从1898年Liocourt De运用等比级数来构建异龄林直径结构模型开始，许多函数模型被用来模拟森林直径分布状况，如Pearsonian曲线，负指数函数[3-5]，gamma分布，三参数对数正态分布[6]，β分布，Weibull分 布[1]，Jonson的 SB 分 布[7]等， 其 中Weibull分布运用的最为普遍[8-13]。然而，有的林分经历过度采伐或遭受森林火灾后，直径分布由简单的单峰或反J型结构转变为复杂的双峰或不规则结构，用单一的函数并不能进行准确的模拟[14-17]。对此，不少学者提议运用混合分布模型来描述这些林分直径分布[18-19]。近来，Liu等介绍了一种限定混合Weibull分布模型，并对比单个三参数Weibull函数和负指数函数，来模拟不规则、多峰或具有明显偏度的直径结构分布，发现限定混合Weibull模型能获得更高的精度，具有更好的模拟效果[16,20]。对于具有不规则直径结构的异龄林，限定混合Weibull分布模型得到了较为广泛的应用[2,21-23]。

长白山云杉冷杉林(主要是臭冷杉Abies nephrolepis、 鱼 鳞 云 杉Picea jezoensis var.microsperma和红皮云杉Picea koraiensis形成的混交林)是我国重要的用材林(尤其是红皮云杉)和风景林，同时发挥着涵养水源、保持水土的重要效应[24]。然而，从19世纪末开始，长白山林区经历了不同程度的采伐，火灾和拓荒等各种形式的干扰，原来较简单的林分结构遭到破坏，取而代之的是大量具有不规则林分结构的森林群落[25]，其直径分布结构复杂。研究伐后云冷杉林的林分结构，分析其直径分布特点等，对于我们正确认识、合理经营森林资源，促进其形成稳定健康的森林群落具有重要意义。以往对于长白山森林的直径结构的描述，大多采用单一的函数模型进行分析[9,11,26-27]。本文利用限定混合Weibull函数对6块云冷杉样地的直径调查数据进行研究，并采用负指数函数、Weibull分布函数进行模拟，对比3者模拟结果，以期准确分析云冷杉的直径结构特点，客观科学的评价森林资源，为森林的经营管理发挥一定的理论指导作用。

1 研究区概况及研究方法

1.1 研究区概况

研究区位于长白山金沟岭林场(130°10′E，43°22′N)，海拔 300 ～ 1200 m，受季风影响，属温带大陆性山地气候，土壤为针叶林灰棕壤。全区林分中，云冷杉林是分布最广的森林类型，占森林面积的80%，现有的多数云冷杉林是原始林经过30%～60%的择伐后形成的[25]。

本文选取如下群落：于1986年设立的云冷杉过伐林25号、27号、28号固定样地，面积均为0.2 hm2，样地至今遭受2～3次不同强度的采伐。样地基本保证2年复测一次。样地25号和28号选取2008年的调查数据，27号选取2007年数据。近原始林20号固定样地，1986年设立于44林班4小班，面积0.2 hm2，该林分受破坏程度较低，基本保持原始林相，已连续复测12次，选取2008年调查数据。1978年设置的云冷杉针阔混交林局级2号和5号样地，面积均为0.5 hm2，已调查17次，至今没进行过采伐作业，选取2007年调查数据。云杉Picea koraiensis、冷杉Abies nephrolepis、红松Pinus koraiensis为6个样地的主要树种，其中还有部分色木Acer mono、紫椴Tilia amurensis、枫桦Betula costata、白桦Betula platyphylla、蒙古栎Quercus mongolica、榆树Ulmus pumila等。

1.2 研究方法

每两年对6块样地调查一次，对样地内胸径≥5 m的乔木进行每木检尺，记录调查木的树种名，胸径、树高、冠幅、第一枝下高和坐标位置。

本文采用负指数函数，三参数Weibull分布函数和限定混合Weibull分布函数对6块样地的直径分布结构进行模拟。

负指数函数为[3,27]：

三参数Weibull分布密度函数为：

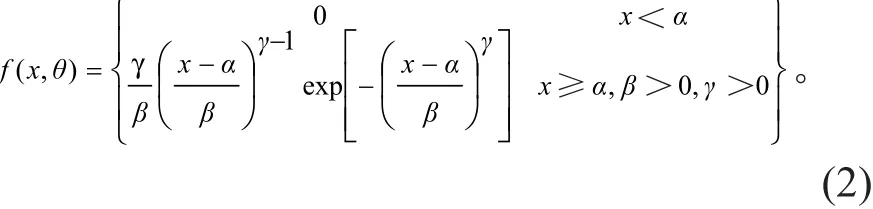
式 (1)～ (2)中 θ=(α，β，γ)′，α，β，γ分别为位置(直径分布最小径阶下限值)，尺度，形状参数。

假定一个混合分布模型由k个组分组成，其中第i个组分为特定的概率密度函数，fi(x)为一般概率密度函数表现形式，则混合分布模型可表示为：

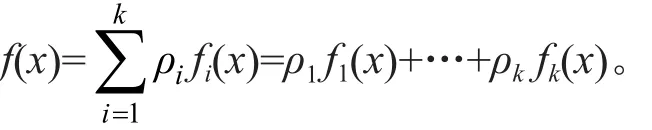
式中ρ1为第i个组分占总分布的比例，满足：

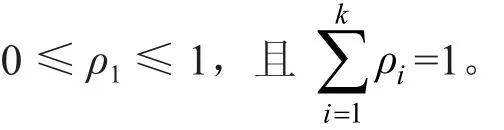
本文视f1(x)，……，fk(x)为概率密度函数，不同组分有不同的变量，平均值，标准差，并限定 fk(x)为三参数 Weibull函数 (X～Weibull(α，β，γ))。同时只考虑2个组分，即k=2。限定混合模型为：

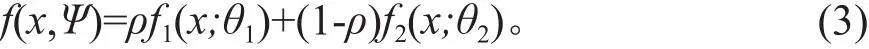
式 (3)中：ψ=(ρ，θ1，θ2)，θ1=(αi，βi，γi)′，i=1 或 2；0≤ρ≤1；方程共有7个参数，即两个组分的位置，形状，尺度参数 (α1，β1，γ1，α2，β2，γ2)和比例参数ρ。

公式(1)和(3)为概率密度函数，株数估计值Ni=N[F(Xi+ω)-F(Xi-ω)]，其中 N为总株数，F(x)为概率累计函数，Xi为第i径阶中值，ω为组距除以2。方程(2)为计算第i径阶的树木株数，α、β为直径分布特征的参数。

估算三参数Weibull函数参数的方法有：最大似然估计法[9]、最小二乘法[8]、百分位数法、线性求解法[28]和近似估计法、改进单纯形法等，其中以最大似然估计法最为精确，从而得到广泛应用[1,9,16,29]。根据统计软件SPSS 18.0和ForStat 2.0来估算方程1和2的参数，运用R软件（2.15.1版）中mixdist软件包，根据最大似然估计法并结合Newton-type算法和EM算法求出限定混合模型的参数[2,16,20-21]。

统计量均方根误差(RMSE)、平均误差(Bias)作为不同模型的比较标准，似然比χ2检验来检验模型的适合度[2,20,22]。定义其中Nj为第j个径阶实测的株数为估计的株数，Rj为实测值与模型模拟的估计值之间的残差。

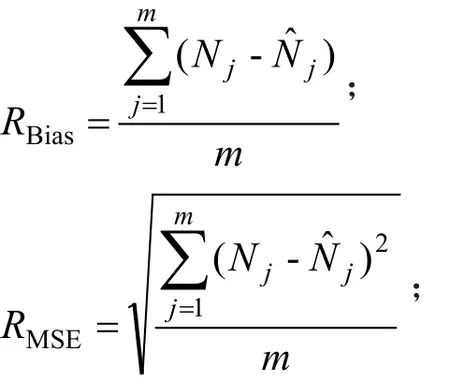
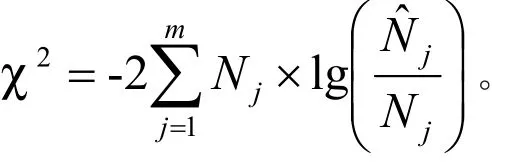
式中，m为径阶数，χ2的自由度为(m-k-1)，k为参数个数。

2 结果与分析

2.1 林分直径结构特征

云冷杉林的基本统计量表明(表1)，28号样地的株数密度最大，为1 020为株·hm-2。6块样地中最大胸径、平均胸径和每公顷胸高断面积的最大值都出现在近原始林20号样地，其直径标准差也表现最大，为14.52。而近年经历过采伐的25号、27号和28号样地的平均胸径、直径偏度和峰度都相对偏小。所有样地的偏度值都大于0，为右偏态，反映样地小于平均胸径的株数较多，而所有峰度值小于0，说明直径分布形态较正态分布平坦。

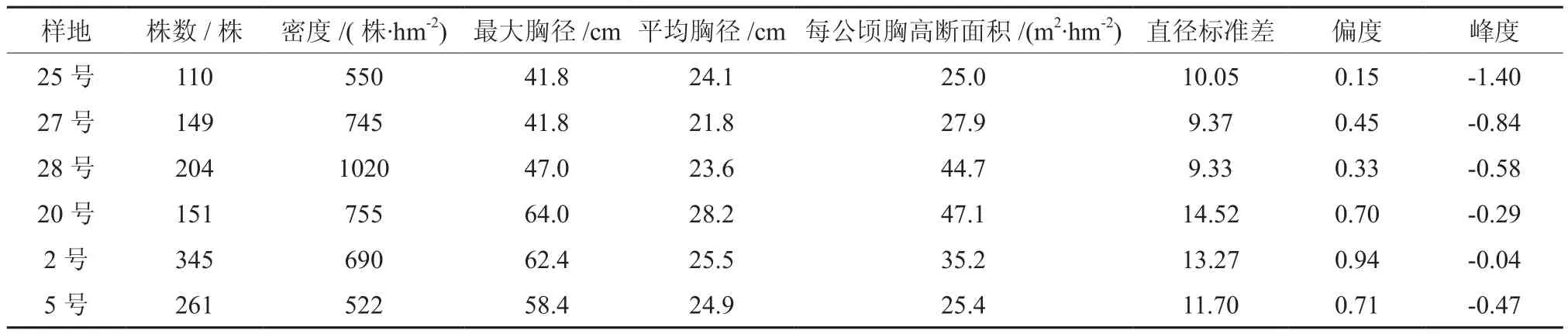
表1 云冷杉样地的基本概况Table 1 Basic characteristics of spruce-fir forest plots

2.2 直径分布拟合与检验

表2显示了3种模型对6块样地直径结构的模拟参数值，以5 cm为起测胸径，体现在模型上则两种Weibull分布的位置参数为5，以2 cm为径阶划分的组距。限定混合Weibull分布中的ρ值与图1中直径分布划分两个部分后各自所占比例相一致。两种Weibull分布中的形状参数值(即γ、γ1和γ2)基本在1～3.6范围内，说明了其拟合曲线为正偏的山状曲线。

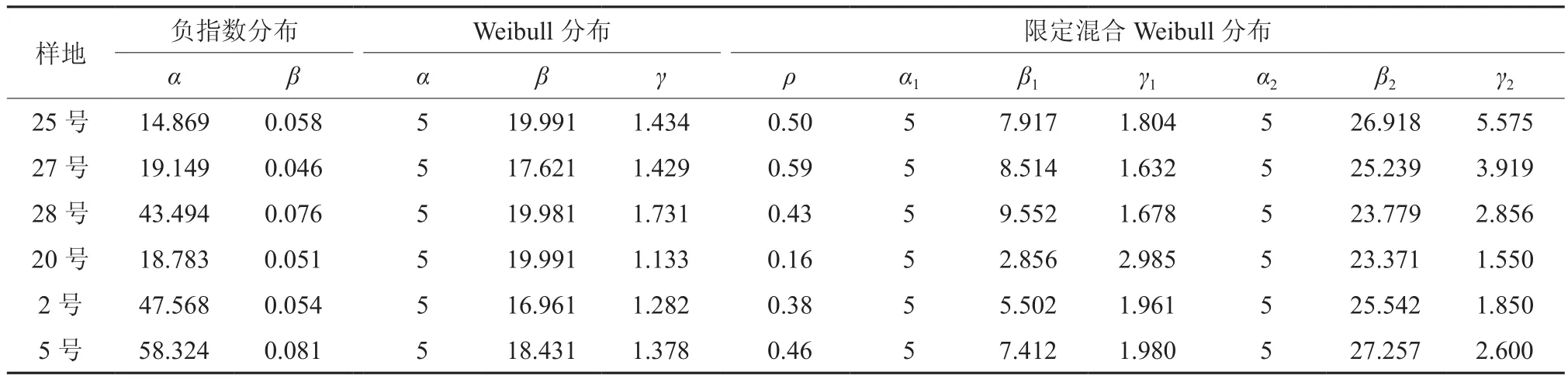
表2 各样地的模型参数值Table 2 Model parameter values of three models for each plot

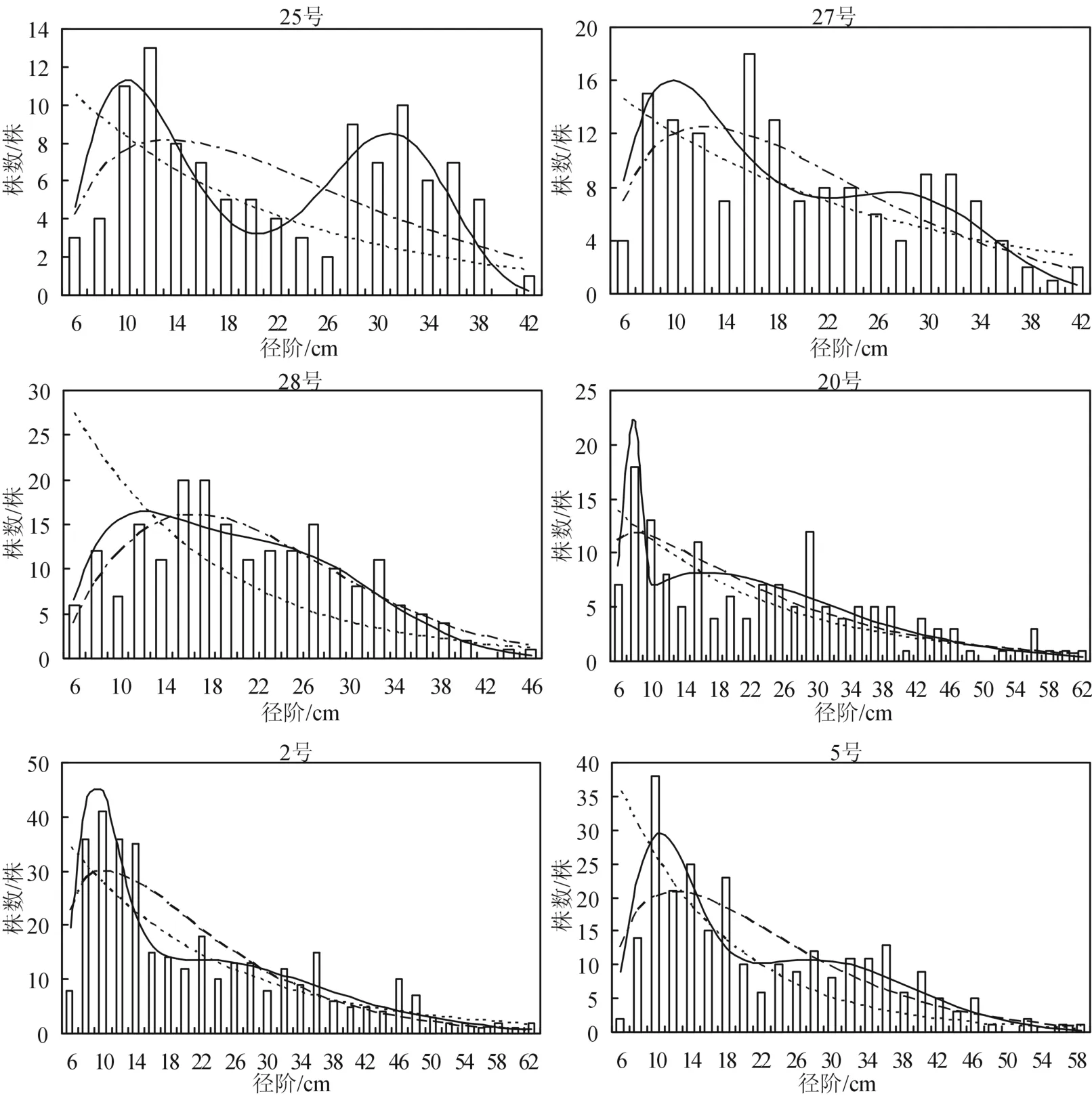
图1 各样地的直径分布观测值和不同模型的估计值Fig.1 Observed and predicted diameter distributions of different models for each plot

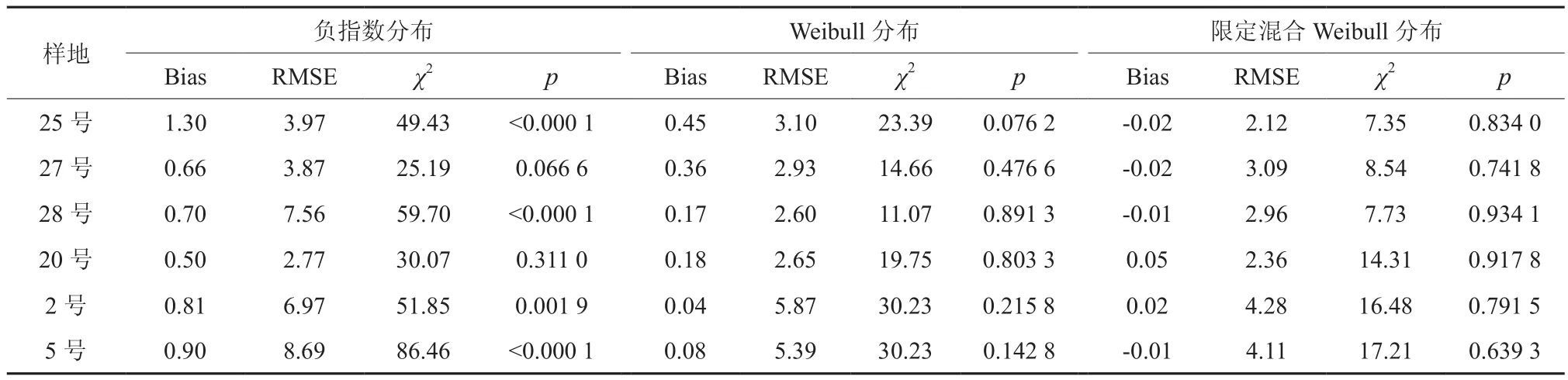
表3 各样地直径分布函数模型的拟合结果检验Table 3 Fitting statistics of diameter distribution models for each plot

图1为6块样地的直径分布直方图和3种分布函数的模拟曲线，表3显示了对不同分布函数的适用性检验结果。25号样地的直径分布为明显的双峰分布，峰值分别在12 cm和32 cm处，直观显示限定混合Weibull分布能对其较好的模拟，而负指数分布曲线则忽略了分布情况。表3中Bias、RMSE和χ2值，限定混合Weibull分布的值都最小，而负指数分布最大，Weibull分布居中；其中负指数的检验p值小于0.000 1，限定混合Weibull分布为0.834 0，说明后者的拟合度最优，得到了与图形直观描述一致的结果。27号样地的直径分布极不规则，在8 cm、16 cm和30 cm径阶处的株数较多，Bias、χ2检验与RMSE得到了不同的结果，Bias、χ2检验都显示3种分布中限定混合Weibull分布的检验值最小，而RMSE值显示Weibull分布的最小。

样地28号的株数在16～20 cm径阶处分布集中，整体呈右偏态，胸径小于平均胸径(23.6 cm)较多，图1显示两种Weibull函数都能较好拟合直径分布，限定混合Weibull分布的检验p值达到0.934 1。近原始林20号和局级样地2号、5号的株数峰值出现在8～10 cm处，然后株数随径阶增大呈减少趋势，但在中等径阶处基本相等，从图中直观表现出限定混合Weibull分布能够很好的拟合这分布情况，而Weibull分布忽略了中等径阶处株数变化平缓的部分。χ2检验的p值显示限定混合Weibull分布最高，且明显高于Weibull分布和负指数分布。

从六块样地总体而言，各样地在6 cm径阶处的株数分布都较少，近期遭受过2～3次采伐的3块样地的直径分布情况表现为不规则，图中曲线显示负指数分布难以拟合其分布情况。而近原始样地和局级样地的直径分布曲线在中等径阶处平坦，随后才呈现下降趋势。表3的模型适合度检验表明，6块样地3种模型中限定混合Weibull分布的Bias值和χ2值均为最小，其中Bias的绝对值均小于0.05，而负指数分布的值最大，Bias绝对值均大于0.5。除27号、28号样地中3种模型RMSE值，Weibull分布表现最小外，其它样地中的模型拟合RMSE值大小规律与Bias值、χ2值的一致。

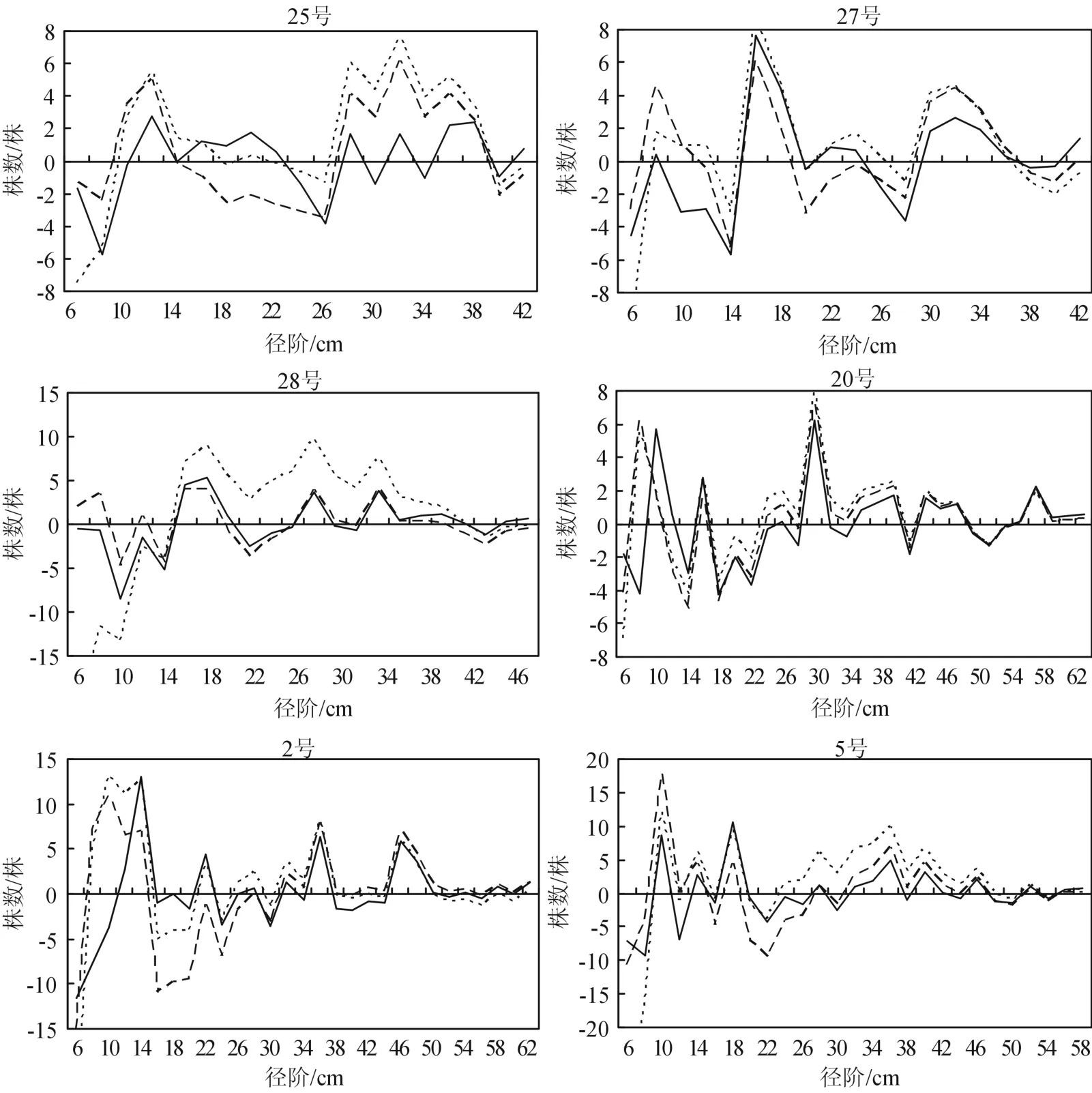
图2 各样地的观测株数与不同模型估计株数的残差Fig.2 Residuals of observed and predicted diameter distributions of different models for each plot

图2的残差图反映了各模型的模拟结果：25号样地中混合限定Weibull分布除8 cm、26 cm径阶处，株数残差值基本在-2到2之间波动，残差相对较小；27号在10 cm处，混合限定Weibull分布高估了其株数，而另两种模型低估了株数；28号样地两种Weibull分布，20号的负指数分布和Weibull分布的残差值在大多径阶范围内表现极为接近；Weibull分布在2号样地的18 cm径阶处，以及5号样地的22 cm处，都过于高估了株数。所有样地中，负指数分布在6 cm径阶处的残差值都相当大；在超过一定径阶(＞28 cm)后，相对于其它两种模型，混合限定Weibull分布的残差值都更接近于0，偏离较少。

3 结论与讨论

(1)云冷杉林是长白山地区地带性植被，对于该森林群落过去执行采育择伐的营林方式，但存在择伐过大的情况[25]。本文从6块样地的基本统计量分析，各样地的乔木密度和每公顷的胸高断面积差异都较大，直径分布直方图表现极不规则，尤其是25号、27号和28号样地，证实了当地森林经历过采伐的经营历史。而近原始林20号样地和局级2号和5号样地的直径分布在中等径阶范围内曲线表现平坦，并不是传统的反“J”形，而呈现 Goff和 West定义的“rotated-sigmoid”[19]，由于中度或强度的人为干扰造成许多大小不等的林隙，林内几乎同时再生出一批树木，当它们达到近熟进入林冠层，生命力强，一段时间内，它们拥有相对高的生长率和低死亡率，此阶段过后成为成熟木，生长减缓，抗干扰能力减弱，死亡率增加，则形成了这种不规则分布[2,19-20]。各样地在6 cm径阶处的株数明显偏少，这种现象的产生可能是因立地遭到人为破坏，导致森林退化；也可能由于外业数据收集过程中人为主观的忽视了起测径阶5 cm左右树木的测量。若为后者，对于各个模型的模拟和评价显然有影响，对此，不少学者采用8 cm或更大径阶作为直径模拟对象[2,20,23,27]。但在分析6块样地历次的测量数据，确认小径阶的株数较少后，本文以6 cm为直径模拟起点，以期客观反映森林生长状况。

(2)采用限定混合模型，并用Weibull函数和负指数函数进行模拟比较。拟合结果图反映出限定混合Weibull函数具有更好的拟合效果，对于直径双峰分布的25号和不规则分布的局2号样地，限定混合模型拟合效果尤为明显。Bias、RMSE和χ2检验从数学统计角度对3种模型进行得出近乎一致的结论，限定混合模型的拟合效果最优，其次是Weibull分布模型，最后是负指数分布模型，此结论与Zhang[20]和Liu[16]研究结果一致。同时，各模型模拟结果的残差图也直观反映了在一定范围内限定混合模型的拟合优势。

(3)本文采用两组分限定混合模型在模拟不规则和多峰直径分布中显示出较好的灵活性和精度，一些学者运用多种统计方法来对比检验多组分的模拟效果[23,30]，发现三组分的Weibull分布拟合效果相对于两组分的并没有显著改善，模型过多组分易造成拟合过程中的收敛效果降低，参数的增加也会使评价标准的卡方降低[2]，认为混合模型组分数不应太多。另外，由于天然异龄林的直径结构复杂，模型各组分拟合部分常出现过度重叠现象，给组分比例的预估带来干扰[21]，因此需要多次代入不同的组分比例值，通过比较最大似然法求得的卡方值，确定最终的组分参数值[20]。

(4)高精度和高灵活性的直径分布拟合模型对于森林经营有重要作用，应逐步探讨不同模型的混合，以及非参数方法的运用。直径分布在森林生长和生产量计算方面有不可或缺的作用，而异龄混交林在整个演替阶段总处于错综复杂的动态过程中，对某一时刻样地的静态描述显然不能满足对于森林的经营规划要求。结合二十几年连续复测打下的良好基础，将来应延续固定样地的复测，构建直径结构动态变化数据，客观全面的分析森林生长规律。

[1] Bailey R L, Dell T R. Quantifying diameter distributions with the Weibull function[J]. Forest Science, 1973, 19(2): 97-104.

[2] Jaworski A, Podlaski R. Modelling irregular and multimodal tree diameter distributions by finite mixture models: an approach to stand structure characterisation[J]. Journal of Forest Research,2012, 17(1): 79-88.

[3] Meyer H A. Structure, growth, and drain in balanced unevenaged forests[J]. Journal of Forestry, 1952, 67: 85-92.

[4] Murphy P A, Farrar R M. A test of the exponential distribution for stand structure definition in uneven-aged loblolly-shortleaf pine stands[M]. USDA Forest Service Research Paper SO-164,1981.

[5] Leak W B. The J-shaped probability distribution[J]. Forest Science, 1965, 11(4): 405-409.

[6] Bliss C I, Reinker K A. A lognormal approach to diameter distributions in even-aged stands[J]. Forest Science, 1964, 10(3):350-360.

[7] Hafley W L, Schreuder H T. Statistical distributions for fitting diameter and height data in even-aged stands[J]. Canadian Journal of Forest Research, 1977, 7(3): 481-487.

[8] 方精云, 菅 诚. 利用Weibull分布函数预测林木的直径分布[J]. 北京林业大学学报, 1987(3): 261-269.

[9] 孟宪宇. 使用Weibull函数对树高分布和直径分布的研究[J].北京林业大学学报, 1988(1): 40-48.

[10] Podlaski R. Diversity of patch structure in Central European forests: are tree diameter distributions in near-natural multilayered Abies-Fagus stands heterogeneous?[J]. Ecological Research, 2010, 25(3): 599-608.

[11] 龚直文, 亢新刚, 杨 华, 等. 长白山杨桦次生林直径结构研究[J]. 西北林学院学报, 2009(3): 1-6.

[12] 李 俊, 佘济云, 胡焕香, 等. 昌化江流域天然林直径结构研究[J]. 中南林业科技大学学报, 2012, 32(3): 37-43.

[13] 曾思齐, 李 俊, 李东丽, 等. 南方集体林区南酸枣次生林林分结构研究[J]. 中南林业科技大学学报, 2012, 32(4): 1-6.

[14] Tham S. Structure of mixed Picea abies (L) Karst, and Betula pendula Roth and Betula pubescens Ehrh. stands in South and middle Sweden[J]. Scandinavian Journal of Forest Research,1988, 3:355-370.

[15] Maltamoa M, Kangasb A, Uutterac J, et al. Comparison of percentile based prediction methods and the Weibull distribution in describing the diameter distribution of heterogeneous Scots pine stands[J]. Forest Ecology and Management, 2000, 133(3):263-274.

[16] Liu C, Zhang L, Davis C J, et al. A finite mixture model for characterizing the diameter distributions of mixed species forest stands[J]. Forest Science, 2002, 48(4): 653-661.

[17] Podlaski R, Zasada M. Comparison of selected statistical distributions for modelling the diameter distributions in nearnatural Abies-Fagus forests in the witokrzyski National Park(Poland)[J]. European Journal of Forest Research, 2008, 127(6):455-463.

[18] Falls L W. Estimation of parameters in compound Weibull distribution[J]. Technometrics, 1970, 12(2): 399-407.

[19] Goff F G, Weas D. Canopy-understory interaction effects on forest population structure[J]. Forest Science, 1975, 21(2): 98-108.

[20] Zhang L, Gove J H, Liu C, et al. A finite mixture of two Weibull distributions for modeling the diameter distributions of rotatedsigmoid，uneven-aged stands[J]. Canadian Journal of Forest Research, 2001, 31(9): 1654-1659.

[21] Zasada M, Cieszewski C J. A finite mixture distribution approach for characterizing tree diameter distributions by natural social class in pure even-aged Scots pine stands in Poland[J]. Forest Ecology and Management, 2004, 204(2-3): 145-158.

[22] Zhang L, Liu C. Fitting irregular diameter distributions of forest stands by Weibull, modified Weibull, and mixture Weibull models[J]. Journal of Forest Research, 2006, 11(5): 369.

[23] 王顺忠, 王 飞, 张恒明, 等. 长白山阔叶红松林径级模拟研究——林分模拟[J]. 北京林业大学学报, 2006(5): 22-27.

[24] 《中国森林》编辑委员会. 中国森林(第2卷):针叶林[M].北京: 中国林业出版社, 1999.

[25] 李冬兰, 于政中, 亢新刚. 检查法第一经理期研究[J]. 林业科学, 1996(1): 24-34.

[26] 吕康梅. 长白山过伐林区云冷杉针阔混交林最优林分结构和最优生长动态的研究[D]. 北京林业大学, 2006.

[27] 张 青, 赵俊卉, 亢新刚，等. 基于长期历史数据的直径结构预测模型[J]. 林业科学, 2010(9): 182-185.

[28] 亢新刚, 胡文力, 董景林, 等. 过伐林区检查法经营针阔混交林林分结构动态[J]. 北京林业大学学报, 2003, 25(6): 1-5.

[29] Cohen A C. Maximum likelihood estimation in the Weibull distribution based on complete and on censored samples[J].Technometrics, 1965, 7(4): 579-588.

[30] Wolfe J H. Comparative cluster analysis of patterns of vocational interest[J]. Multivariate Behavioral Research, 1978, 13(1): 33-44.

Simulation of multi-peaks and irregular diameter distributions by finite mixture models: a case study on spruce-fir forests in Changbai Mountain

DU Zhi1, KANG Xin-gang1, YUE Gang1, XU Guang2, ZHAO Dong-ning2, YANG Yi-jun2, GAO Xiang2

(1.Key Laboratory for Silviculture and Conservation of Ministry of Education, Beijing Forestry University, Beijing 100083, China;2. Wangqing Forestry Bureau, Wangqing 133200, Jilin, China)

Based on the investigation data from six example plots in Changbai Mountain in northeastern China, the finite mixture Weibull model was applied to simulate the tree diameter distribution with. the results of traditional methods of negative exponential model and Weibull model as the comparisons. The results show that the tree diameter distributions of six plots were presented irregular shapes of multi-peaks, rotated-sigmoid, etc.. The statistics show the fitting effect of finite mixture Weibull model was the best, especially in modelling bimodal and rotated-sigmoid distributions, then was the Weibull model’s, and negative exponential model’s was the last.The residual figure displays the residual value of finite mixture model more close to zero than others. The finite mixture model was a better alternative method, with high flexibility and precision to model tree diameter distribution.

spruce-fir stands; diameter distribution; finite mixture Weibull model; negative exponential model; Weibull model

S758.5；S791.14

A

1673-923X(2013)04-0043-07

2012-09-25

国家“十二五”科技支撑项目——阔叶红松林和云冷杉过伐林可持续经营技术与示范(2012BAD22B2)；国家林业局948项目（2013-4-66）

杜 志（1986-），男，湖南长沙人，硕士研究生，主要从事天然林结构方面的研究；E-mail：duzhi6880448@163.com

亢新刚（1952-），男，北京人，教授，主要从事天然林结构和生长以及经营管理的研究；E-mail：xingangk@163.com

[本文编校：吴 彬]