基于混合整数规划模型的木材物流网络优化

陈 诚，邱荣祖

（福建农林大学 交通学院，福建 福州 350002）

基于混合整数规划模型的木材物流网络优化

陈 诚，邱荣祖

（福建农林大学 交通学院，福建 福州 350002）

结合木材物流的实际，在对现有木材物流网络分析的基础上，将木材物流中心选址和木材运输方案制定结合起来考虑，从木材物流网络全局角度考虑这两个决策问题，建立了木材物流网络优化的混合整数优化模型。该模型以木材物流网络总成本最小为目标，确定木材物流中心的数量和位置，并明确每个需材点的运输方案。针对混合整数规划模型求解的难度，利用Lingo软件包对该模型进行了编译求解，以永安林业（集团）股份有限公司的木材物流网络优化为算例进行应用分析，优化结果显示了模型和算法的科学性及实用性。

木材物流；物流网络优化；混合整数规划

林业属于资源型产业，在国民经济建设、人民生活和生态环境保护中，均有着特殊的地位和作用。近年来，生态环境保护日益重视，林产品加工业的不断发展，原材料需求不断加大，生物质利用技术的不断成熟等都对木材物流系统提出了更高的要求。木材物流网络的优化设计是木材物流系统中的重要问题之一，但由于木材商品的特殊性，木材物流成本居高不下，如何降低木材物流成本，提高木材物流效率成为亟待解决的突出问题。

木材运输费用占木材物流系统总费用的比重较大[1]，木材运输费用的降低必须有完善的木材物流网络的支撑，但目前针对木材物流系统的研究较少。文献[2]构建了伐区运输路线优化模型，确定了伐区木材运输的最优路线，但其研究仅仅局限于木材集材阶段的运输路线的选取。文献[3]建立了木材直达、中转混合运输问题的数学模型，并采用遗传算法进行求解，从而确定从供材点至需材点的合理运输方案；该文献是在已有物流网络的基础上进行运输方案的确定，并未考虑现有物流节点的合理化问题。文献[4]和文献[5]分别利用遗传算法以及ArcGIS与遗传算法相结合的方法进行了木材物流中心选址问题的研究，仅考虑木材从供材点汇集到木材物流中心，再从木材物流中心分流到各个需材点的情况，未考虑木材从供材点直接运送到需材点的情况。

物流网络的优化包括三个问题的优化：节点的数量、节点的位置以及节点的服务对象[6]。因此，本文将从木材物流网络全局的角度进行规划，整合木材运输和木材物流中心选址问题，建立木材物流网络优化模型。由于木材资源分布、客户分布、供需状况、道路网络、地价水平和自然条件等因素的影响，木材物流网络优化问题往往比较复杂。由于物流系统中的物流变量不一定都是整数，故通常运用混合整数规划法建立优化模型[7]。

1 木材物流网络分析

木材在伐区点被伐到后，经过集材被运输到伐区楞场，然后从伐区楞场被运往需材点或者是木材物流中心。选材作业既可在伐区完成，也可在木材物流中心进行，如果需求种类单一、不需进一步加工（如去皮等）且需求量较大的需材点采用的物流模式是从伐区楞场、甚至是砍伐点直接运送到需材点，此时运输方式基本为公路运输，成本相对较高。如果是需要进一步加工或是需要和其他材种（可能由其他供材点供应）混合运输的木材的物流模式则是从伐区楞场运输到木材物流中心，然后再从木材物流中心运往需材点。木材物流网络结构如图1所示（图1中的供材点可视为伐区楞场），与大多数其他商品的物流网络不同，木材物流网络的三级结构间均互为多对多的关系，是一种较为复杂的混合物流网络。

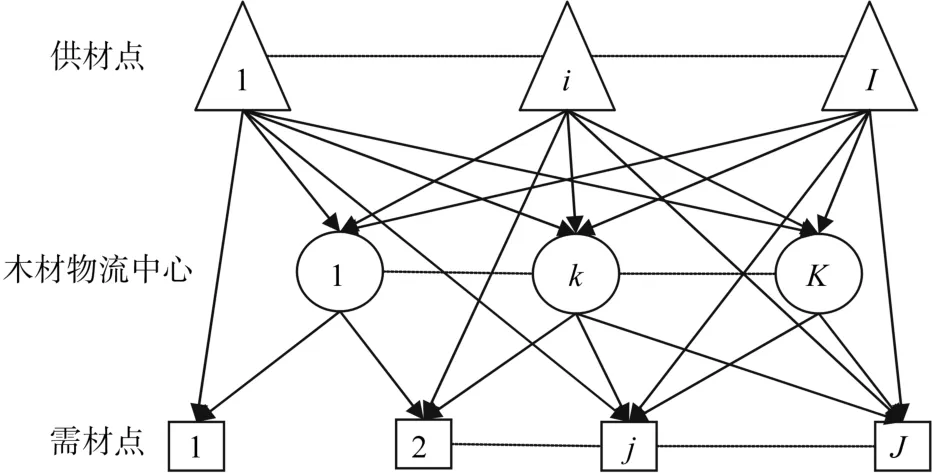
图1 木材物流网络Fig. 1 Logistics network of timber

木材物流网络包括从伐区楞场到木材物流中心的运材过程、从木材物流中心到需材点的运材过程以及从伐区楞场到需材点的运材过程。因此，木材物流网络的优化包括确定木材物流中心的位置、数量、规模以及明确各需材点的运输方案。

2 木材物流网络优化模型

建立基于图1所示的木材物流网络结构的混合整数规划模型。

2.1 模型假设

（1）在实际操作中，每个采伐点的出材率是在采伐前就预先设计好的，建模时认为每个供材点的材种和供应量为已知。

（2）在木材物流系统中，主要的需材点为各类加工厂（如：锯木厂、人造板厂、纸浆厂等），这些工厂的地理位置和年需求量也是相对固定的，故假设需材点的地理位置、所需材种和需材量已知。

（3）木材物流中心对于场地有一定的要求，因此木材物流中心的潜在地理位置仅在一定的备选范围内选择，并设定每个备选地点的吞吐能力，即本文中的木材物流中心选址问题属于离散型选址模型，而目前离散型的选址模型是研究的重点[8]。

（4）木材商品的表现形态有多种（如：原木、薪材等），即本文研究的木材物流网络为多产品物流网络。

2.2 目标函数

木材物流网络优化的目标函数是使总物流费用最小，包括从供材点到木材物流中心的运输费用、供材点到需材点的运输费用、木材物流中心到需材点的运输费用、木材物流中心的固定费用以及木材物流中心的中转费用。各运输区间的单位运输成本为最佳运输路径前提下的取值；木材物流中心的固定费用为基本建设费用在投资回收期内的年值与年经营费用中的固定成本之和；木材物流中心的中转费用为单位木材中转费用的变动成本。

令I表示供材点集合，K表示木材物流中心集合，J表示需材点集合，H表示材种集合。可建立如下的木材物流网络优化的目标函数：

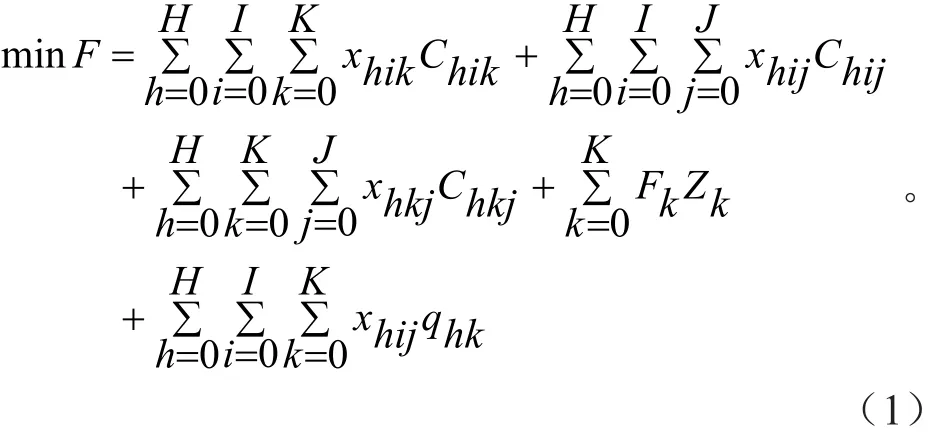
式（1）中：xhik为从供材点i运送到木材物流中心k的第h种木材的数量，m3；Chik为从供材点i到木材物流中心k运送第h种木材的单位运输成本，元/ m3；xhij为从供材点i直接运送第h种木材至需材点j的数量，m3；Chij为从供材点i直接运送第h种木材至需材点j的单位运输成本，元/ m3；xhkj为从木材物流中心k运送第h种木材至需材点j的数量，m3；Chkj为从木材物流中心k运送第h种木材至需材点j的单位运输成本，元/ m3；Fk为木材物流中心k的建设成本，元；Zk为0、1变量，Zk=1表示第k个木材物流中心被选中，Zk=0，表示第k个木材物流中心未被选中；qhk为木材物流中心k第h中木材的处理成本。

2.3 约束条件

2.3.1 供材点供应能力限制

每个供材点因其伐区经营面积限制，因而其供应能力是有限制的[9]。

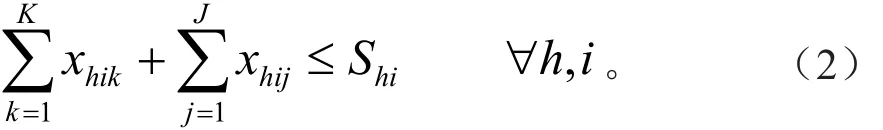
式（2）保证了从每个供材点流向木材物流中心和需材点的每种木材量之和小于等于该供材点的能力约束。

2.3.2 需材点需求满足约束

每个需材点的需求要应该被满足。

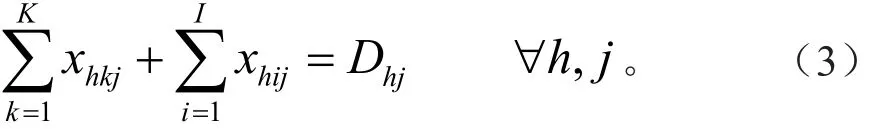
式（3）保证了每个需材点从供材点和木材物流中心获得的每种木材量之和等于该需材点的需求量。

2.3.3 木材物流中心能力限制

每个备选木材物流中心有容量限制，且木材物流中心只有被选中，才能投入使用。在每一木材物流中心每种木材的流入量均应不小于该种木材的流出量。

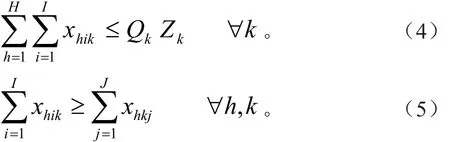
式（4）保证流入每一木材物流中心的所有材种的总量小于木材物流中心的吞吐量，式（5）保证每个木材物流中心的每种材种的流入量均大于等于流出量。

2.3.4 运量约束

只有当木材交易量较大时，才会在供材点进行交易并直接从供材点运往需材点，需要对从供材点直接运往需材点的木材量进行数量约束。

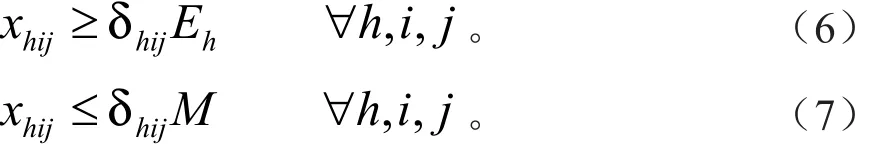
式（6）～（7）中：δhij为0、1变量，表明供材点i和需材点j之间是否存在；Eh为设定的每种产品在供材点的直接发货的最小数量；M为一较大整数，远大于各需材点的需求数量。

式（6）和式（7）保证了每种木材从供材点直接运往需材点的数量为一大于最小直接供货数量的值，否则该值为零。

2.3.5 变量约束

式（8）为变量的非负约束，式（9）为0、1变量约束。

3 模型求解

本文构造的木材物流网络优化模型能为实际应用提供可操作的工具，但因模型的变量多，约束条件多，求解较为困难。Lingo软件是美国LINDO公司开发的一种专门用于求解最优化模型的软件包，它使用分支定界法求解整数和混合整数规划问题，执行速度快，输入方便，易于求解和分析大规模优化问题[10]。本文以Lingo软件包为基础，设计了求解本文构建的木材物流网络优化混合整数规划模型的程序，能迅速有效的求出模型的全局最优解。

4 实例应用

以永安林业（集团）股份有限公司的木材物流现状为背景，研究其木材物流网络优化问题。永林集团目前拥有5个采育场（福溪、福庄、半村、大坑、虹桥）和2个采购站（燕江、小陶），组成了木材物流网络的7个供材点，主要提供原木和薪材两种产品。永安人造板厂、永林蓝豹、永安福星、青山纸业、福州福人组成了5个需材点。从土地条件、交通基础设施、竞争对手、自然条件等因素出发，利用GIS软件获得4个木材物流中心的候选位置。用Si（i＝1，2，…，7）表示供材点，Di（i＝1，2，…，5）表示需材点，Li（i＝1，2，…，4）表示备选木材物流中心，Ti（i＝1，2）表示材种。供材点的供应量、需材点的需要量、木材物流中心的规模限制，以及三者间不同材种的单位运输费用如表1～表5所示。直送起运点设为8 000。

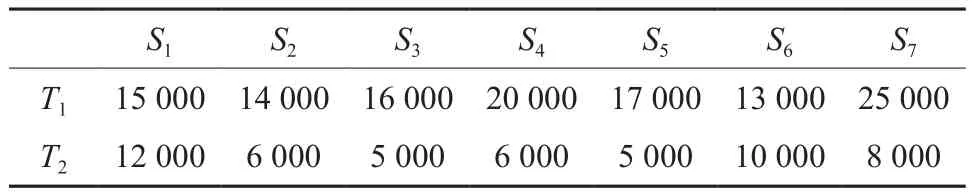
表1 供材点的供应量Table 1 Supply quantity of timer supply centers

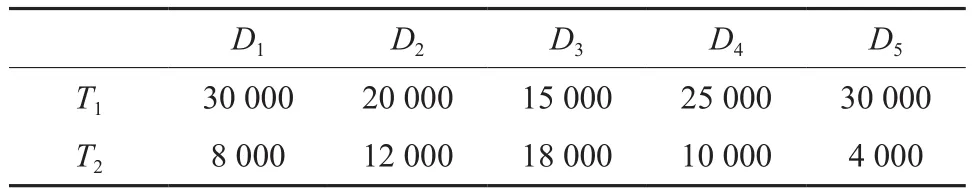
表2 需材点的需要量Table 2 Demand quantity of timer demand units

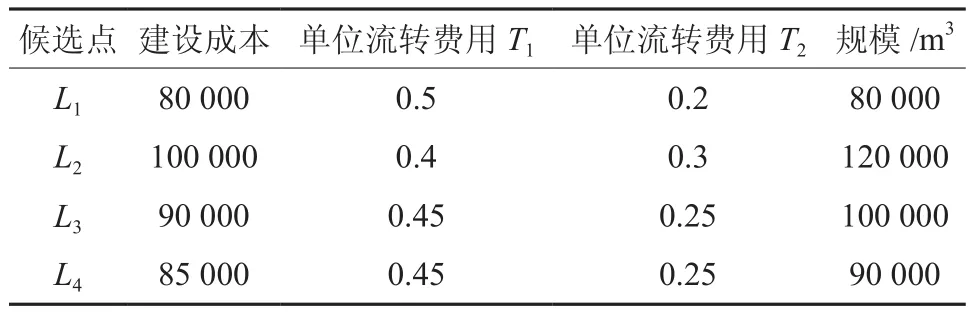
表3 候选点建设成本、规模及流转费用Table 3 Construction cost, scale and transfer cost of candidate logistics centers

利用Lingo对模型进行编译求解，在AMD Athlon（tm） 64 X2 Dual Core Processor 4400+2.31GHz，2.87GB的电脑上运行，经过2723次迭代获得全局最优解，运行时间为1 s，选择第四个候选点为木材物流中心，总成本为926 550元。木材物流网络优化结果如图2所示。

表4 候选点与供材点和需材点间的单位运输费用Table 4 Unit transportation cost between candidate logistics center and supply and demand sites

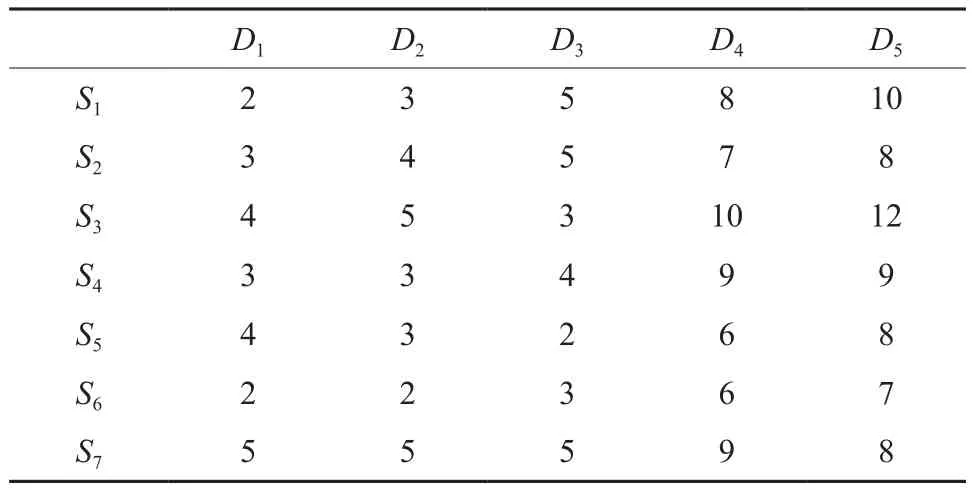
表5 供材点与需材点间的单位运输费用Table 5 Unit transportation cost between supply and demand sites

图2显示了在备选位置中选择一处建设木材物流中心，即4号备选地，并明确了木材物流网络中两种产品的运输方案。

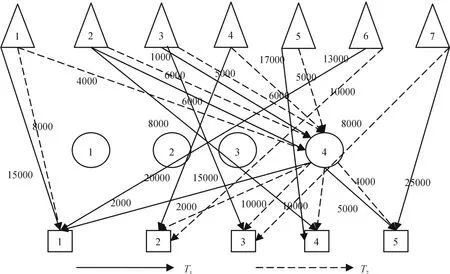
图2 求解结果示意Fig.2 Result of optimaztion

5 结 语

从物流网络全局角度，整合设施选址和运输问题，进行整体优化，不仅能同时解决两个决策问题，而且在选址的同时考虑运输方案的制定，使选址结果更符合实际，从而使整体物流网络得到更进一步的优化。本文研究了整合设施选址和运输方案制定的木材物流网络优化问题，以物流网络总成本最小为目标函数，建立了木材物流网络优化的混合整数规划模型，通过模型求解，确定了木材物流网络中合理的物流中心数量、位置以及优化的运输方案；所得结果为木材物流网络的构建及优化提供了有益的决策参考。

在实际运作中，木材物流网络中的供材点的数量、木材供应的品种和数量以及需材点的数量、需求品种及需求数量会随着时间的变化而发生变化的，而木材物流中心的位置一经选定则不容易发生变化，进一步的研究将在木材物流网络的规划和优化中考虑网络中各参数的动态变化。

[1] Dick Carlsson, Mikael Rönnqvist. Supply chain management in forestry-case studies at Södra Cell AB [J]. European Journal of Operational Research, 2005, 163(3): 589-616.

[2] 张淑芬，邢艳秋，吴红波，等．基于GIS和RS技术的木材运输线路优化研究——以吉林省汪清林区为例[J]．森林工程，2011，27(2):48-51．

[3] 刘娜翠，邱荣祖．基于遗传算法的木材运输方案优化技术[J]．福建林学院学报，2010，30(4):380-384．

[4] 林雅惠，钟晓燕，钟聪儿，等．基于遗传算法的木材物流中心选址研究[J]．运筹与管理，2007，16(6) :51-56．

[5] 邱荣祖，林雅惠，钟聪儿．基于ArcGIS 的木材物流中心选址[J]．林业科学，2010，46(6):113-117．

[6] 物流网络可靠性优化的双目标机会约束规划模型与算法[J]．中南林业科技大学学报，2011,31（9）：160-164.

[7] 庞 燕，王忠伟．基于混合整数规划模型的农产品物流网络优化[J]．中南林业科技大学学报，2010，30(9):91-94．

[8] Fellowsa M R, Fernau H. Facility location problems: a parameterized view [J]. Discrete Applied Mathematics, 2011,159(11): 1118-1130.

[9] Juan J. Troncoso, Rodrigo A. Garrido. Forestry production and logistics planning: an analysis using minxed-integer programming [J]. Forest policy and Economics, 2005, 7(4):625-633.

[10] 谢金星，薛 毅．优化建模与LINDO／LINGO软件[M]．北京：清华大学出版社，2005．

Optimization of timber logistics network based on mixed-integer planning model

CHEN Cheng, QIU Rong-zu
(School of Transportation , Fujian Agriculture and Forestry University , Fuzhou 350002 , Fujian , China)

Considering the practice of timber logistics, a mathematical model of mixed-integer programming for timber logistics network was formulated at the sight of global optimization to solve two common decision problems by combining them: timber logistics center location and timber transportation scheme, which was based on the analysis of current timber logistics network. Aiming at the minimization of total cost of timber logistics network, the number and location of logistics center and the optimal timber transportation scheme can be determined to form the network by solving this model. The proposed model was optimally solved using Lingo, for the diff i culty of mixed-integer programming model to work out. The case of timber logistics network optimization in Fujian Yong’an Forestry (Group) Co. Ltd. was presented and analyzed. The results show the model’s scientif i calness, practicality and effectiveness.

timber logistics; logistics network optimization; mixed-integer planning

S784；F253.4

A

1673-923X(2013)01-0094-05

2012-10-10

福建省教育厅科技项目（JB12078）；福建省教育厅高校专项( JK2010017)

陈 诚（1982-），女，江西樟树人，讲师，博士研究生，从事林业工程、林产品物流系统优化研究

邱荣祖（1961-），男，教授，博士生导师，从事物流技术、3S技术应用研究

[本文编校：欧阳钦]