基于高光谱数据的东洞庭湖苔草LAI估算研究
邱 琳,林 辉,孙 华,臧 卓,莫登奎
基于高光谱数据的东洞庭湖苔草LAI估算研究
邱 琳,林 辉,孙 华,臧 卓,莫登奎
(中南林业科技大学 林业遥感信息工程研究中心,湖南 长沙 410004)
叶面积指数(leaf area index ,LAI)是表征植被冠层结构和光合面积的重要参数。实时动态的植被LAI监测对于诊断植被生长状况及趋势具有重要作用。本研究旨在通过对高光谱数据的数学变换与特征分析,构建东洞庭湖苔草LAI的最佳估算模型。通过分析52组苔草样本640~780 nm波段范围内的反射率、一阶微分及倒数的对数的光谱特征,选择特征波段,运用多元逐步线性回归法与偏最小二乘回归法建立估算模型。研究发现特征波段为707~758 nm,以上3种光谱数据的多元逐步线性回归模型决定系数分别为0.526、0.815、0.565,均方根误差分别为0.320、0.269、0.273,3者偏最小二乘回归模型的决定系数均高达0.9以上,均方根误差分别为0.189、0.262、0.134。结果表明:偏最小二乘回归法优于多元逐步线性回归法,该估算模型可有效估算苔草LAI。
苔草;高光谱;植被类型;LAI;反射率;偏最小二乘回归
叶面积指数(leaf area index,LAI)是重要的生物物理参量,可为植被冠层研究提供结构化定量信息,可准确高效地判断植被生长状况及趋势,亦是各种生态模型及碳循环研究的重要参量,因此具有极其重要的研究意义[1]。遥感估算LAI的方法费用低、宏观性强、资料获取全面,具有客观、定量、准确的优点,成为近年研究的热点[2]。
基于高光谱的植被LAI的估测,已有众多学者从不同的角度和方法,对不同尺度和不同植被类型进行了研究,并取得了突出的成果[3]。许多研究者构造光谱参数,例如归一化植被指数、比值植被指数等不同形式进行植被LAI反演研究[4-7]。近年来,随着高光谱遥感蓬勃发展,导数光谱技术越来越多地用来反演植被叶面积指数[8-10]。研究表明,LAI与一阶微分光谱具有良好的相关性[11],基于光谱曲线分析的红边参数对LAI表现敏感[12-13],对LAI表现最为敏感的是750 nm波段附近的光谱一阶导数,红边面积与红边振幅等三边参数与LAI也有良好的相关性[11,13]。此外,倒数的对数及其微分也逐渐被运用到高光谱的估算模型中,并取得了较好的精度[14-15]。为了提高LAI的估测精度,前人采用了主成分分析法、支持向量机、神经网络等模糊统计方法[16-17]。也有研究人员采用不同的模型构建方法,例如多元逐步线性回归法与偏最小二乘估计法[14]。由于植被的光谱反射特征与岩石、土壤、水体等其它地物有着显著差异,且各植被类型的光谱反射率也迥然不同,因此,基于植被反射率可区分植被类型、长势及估算生物量。研究表明,LAI与近红外波段的光谱反射率相关性良好[11]。然而,虽然LAI估测已广泛运用于植物生态学、植被学以及一些交叉学科[18],但是在湿地植被研究中运用很少,且估算模型精度有待提高。为此,本研究基于东洞庭湖苔草实测反射率光谱,通过数学变换得出一阶微分与倒数的对数,分析以上3种光谱数据与LAI的关系,提取特征波段,构建LAI的高光谱估算模型,为苔草实时、动态、定量监测奠定基础,为东洞庭湖其它植被类型的进一步研究提供依据。
1 材料与方法
1.1 苔草LAI样本的采集
苔草LAI样本的采集在我国典型湿地东洞庭湖进行。本研究共采集苔草样本52组,各样本均匀分布于东洞庭湖研究区。在研究区域内,每次测量前用标签进行定点,以保证光谱测量和叶面积测量位置一致。苔草叶面积的测定采用美国LI-COR公司生产的LAI2000植被冠层分析仪。所有叶面积测量时间都选择在当日北京时间6:30~9:30或16:30~19:30。冠层分析仪设置1个天空光,4个测量目标值,使用15°的遮盖帽,测量时背对阳光进行,遮挡住操作者本身和日光,尽可能避免直射的阳光。
1.2 光谱测定
光谱测定仪器是美国ASD公司生产的ASD Field SpecPro FR型光谱仪,光谱范围为350~2 500 nm,视场角为25°,其中光谱采样间隔1 nm。在每个样点采集光谱之前都进行白板标定,每个测试点采集30条光谱数据。所有的光谱测定均选择在晴朗无风天气,每次测定时间为北京时间10:30~14:30(太阳高度角大于45°)。测量时必须保持探头垂直向下,高度保持在冠层上方1.3 m附近。
1.3 研究的光谱范围
植被对光谱红光波段强烈吸收,强烈反射近红外光,致使光谱反射率在680~760 nm区域呈现陡峭的爬行脊,将其称之为红边(red edge)。红边是表征植被生化成分含量、健康等状况的重要指标。植被红边区域的高光谱反射率特征可用来估算冠层叶片的叶面积指数[19]。研究表明,LAI与光谱反射率在红边波段范围内相关关系显著[11]。故选用640~780 nm波段范围为研究对象。
1.4 光谱数据预处理
1.4.1 均值处理与平滑
对每个样点采集的数据(30条)求平均值,剔除异常点,将求得的均值作为该样点的光谱反射率。光谱曲线上有很多噪声,这是由于光谱仪各波段在能量响应上存在差别引起的,本研究采用5点加权平滑法对均值处理后的光谱数据进行平滑处理,以消除由仪器引起的随机误差并很好地保持光谱原有的特性。其算法[20]如下:

1.4.2 光谱数据的数学变换
光谱一阶微分和倒数的对数是两种常用的光谱数据数学变换方法[21]。对光谱曲线进行一阶微分变换,可以分解并识别重叠的混合光谱,扩大样本之间的光谱特征差异;光谱反射率经倒数的对数变换后,可增强光谱在可见光区范围内的差异,减少因光照条件变化等引起的乘性因素影响。苔草的原始反射率、一阶微分和倒数的对数的光谱曲线分别见图1、图2、图3所示。

图1 苔草反射率Fig.1 Spectral curves of reflectance of Carex
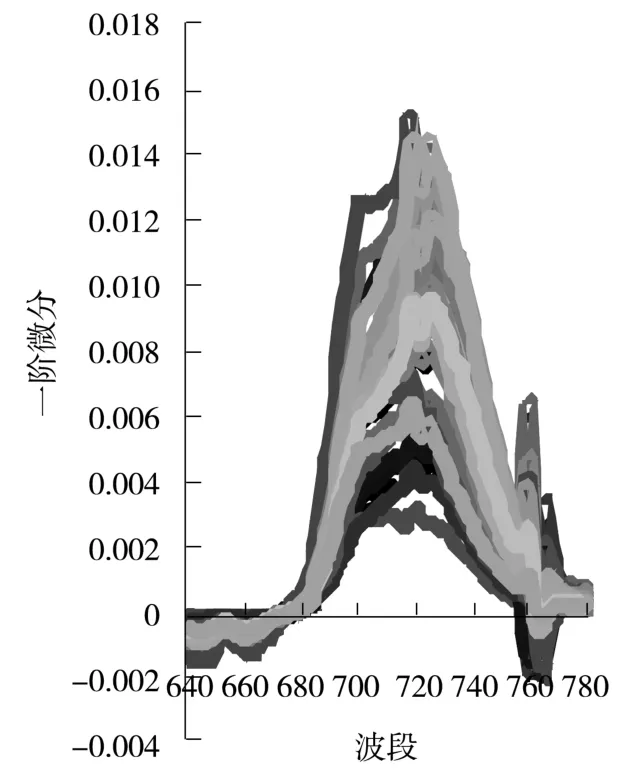
图2 苔草反射率的一阶微分Fig.2 Spectral curves of first derivative reflectance of Carex

图3 苔草反射率倒数的对数Fig.3 Spectral curves of inverse-log reflectance of Carex
由图1可知:(1)在640~680 nm波段范围内,光谱反射率值逐渐减小,光谱反射率曲线呈平缓下降趋势,形成红谷。(2)在680~760 nm附近,光谱反射率值先急剧增大后趋于稳定,光谱反射率曲线形成陡峭的斜坡后接近于直线状态,陡峭的爬行脊即红边。(3)在760~780 nm之间为光谱反射率值高值区,光谱反射率曲线总体趋势平缓,接近于直线状态。
由图2可知:(1)在640~780 nm波段范围内,一阶微分值总体趋势是先增大后减小,一阶微分曲线呈波动状态。(2)在680~760 nm之间,一阶微分曲线出现较明显的双峰。(3)在640~680 nm与750~770 nm波段范围内,一阶微分曲线出现小范围内的波动。
由图3可知:(1)在640~780 nm波段范围内,光谱反射率的倒数对数值先不断增大后急剧减少,最后趋于稳定。(2)在640~680 nm波段范围内,反射率倒数的对数值逐渐增大,曲线呈上升趋势。(3)在680~740 nm波段范围内,光谱反射率倒数的对数值急剧减少,曲线呈现急剧下降的趋势。(4)在740~780 nm之间为光谱反射率倒数的对数低值区,曲线趋势平缓,接近于直线状态。
1.4.3 特征波段选择
对52组苔草反射率、一阶微分及倒数的对数与对应的LAI进行相关分析(如图4、图5、图6所示),结果表明:反射率与LAI在707~780 nm波长范围内呈显著相关,两者的相关性在640~670 nm波段范围内随波长增大而减小,在667~740 nm波段范围内随着波长增大而增大,在740~780 nm波段范围内相关性趋于稳定。大部分波段的一阶微分值与LAI的相关性呈显著相关,两者在640~666 nm波长范围内呈显著负相关,688~758 nm波长范围内呈显著正相关。倒数的对数与LAI在640~654 nm波长范围内呈负相关,655~687 nm范围内呈现正相关关系,688~780 nm波段范围内成负相关,且相关性不断增大,697~780 nm波长范围内呈显著负相关,两者相关性随波长的增大先增大后趋于稳定。综上所述,研究选取的特征波段范围为707~758 nm。

图4 苔草反射率与LAI的相关性Fig.4 Correlation between the reflectance and LAI of Carex
2 结果与分析
2.1 苔草LAI的多元线性逐步回归模型
本研究将52个苔草样本分为两组,将第一组34个样本进行多元逐步回归分析,建立回归模型,第二组18个样本用于模型的精度检验。分别将原始反射率、一阶微分、倒数的对数这3个光谱值的52个波段作为自变量,苔草LAI实测值作为因变量,进行多元逐步回归分析。设定变量方差贡献显著水平0.05作为选入和提出变量的标准,建立苔草LAI高光谱反演模型(Y为苔草LAI含量的反演值)。
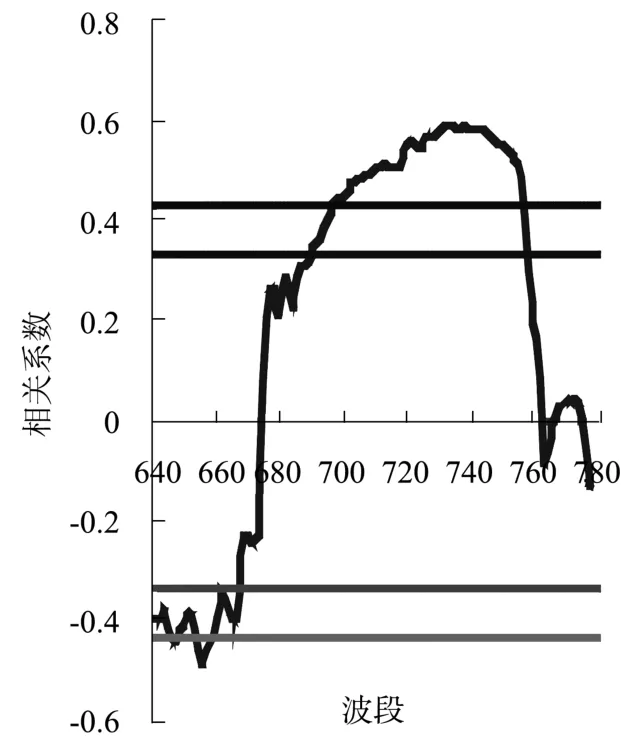
图5 苔草一阶微分与LAI的相关性Fig.5 Correlation between the first derivative reflectance and LAI of Carex

图6 苔草倒数对数与LAI的相关性Fig.6 Correlation between the inverse-log reflectance and LAI of Carex
(1)反射率模型表达式:
Y=5.446-4.213b748+1.110b749,(b748、b749分 别为波长为748、749 nm处的光谱反射率值)。
(2)一阶微分模型表达式:
Y=5.097-12 515.684b739+12 486.84b740,(b739、b740分别为波长为739、740 nm的反射率一阶微分值)
(3)倒数的对数模型表达式:
Y=2.161-2.547b750-0.679b751,(b750、b751分 别为波长为750、751nm的反射率倒数的对数值)。
可以看出,入选波段均是红边范围内波段,且是较为陡峭区域的波段。
表1是苔草LAI多元线性逐步回归模型的检验结果。结果表明,一阶微分与倒数的对数的平均相对误差与均方根误差都比反射率小,说明对反射率进行数学变换有利于特征波段的选择。一阶微分建模的决定系数较高,达0.815。均方根误差最小的是一阶微分,平均相对误差最小的是反射率倒数的对数,这可能是由于光谱进行数学变换后扩大了样本光谱特征之间的差异。

表1 苔草多元线性逐步回归模型检验Table 1 Test results of SMLR model for Carex LAI
图7 为苔草LAI实测值和估算值的对比图,横坐标为苔草实测的LAI值,纵坐标为苔草LAI回归模型的估算值。样点越接近斜率为1的线,说明估算值越接近实测值,模型的反演效果越好。结果表明:一阶微分在多元逐步线性回归模型中反演效果优于反射率和倒数的对数,反演效果较好。
2.2 苔草LAI的偏最小二乘回归模型
运用类似多元线性逐步回归的方法,构建偏最小二乘回归模型并分析。模型的检验结果见表2。
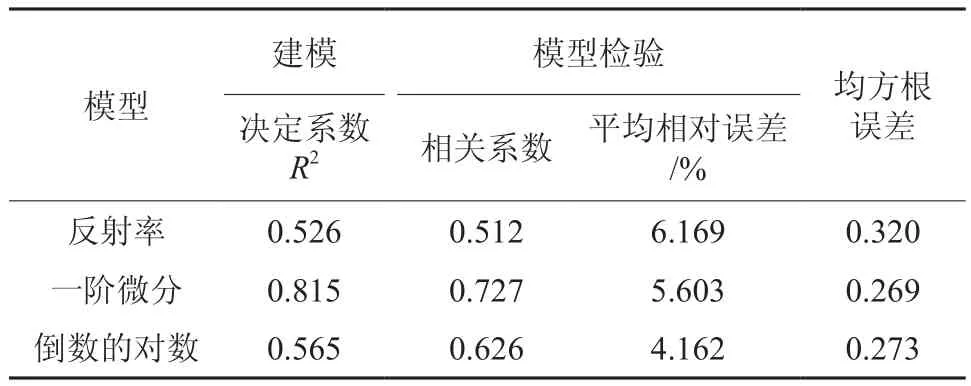
表2 苔草LAI偏最小二乘回归模型检验Table 2 Test results of PLSR model for Carex LAI
从表2分析发现,反射率、一阶微分、倒数的对数这3个模型的建模决定系数均高达90﹪以上,精度高。反射率与一阶微分的平均相对误差分别为3.647﹪、2.679﹪,均方根误差分别是0.189、0.134,实测值与估算值的相关系数分别达0.812、0.894。结果表明:苔草LAI偏最小二乘回归模型中,倒数的对数的模型精度最高,反射率次之,一阶微分相对较差。

图7 苔草LAI多元线性逐步回归模型实测值与预测值的比较Fig.7 Comparison of measured Carex LAI and values estimated by SMLR model
图8 比较了LAI实测值与估算值,分析可得,倒数的对数模型的估算模型精度最高,建模样点和检验样点基本分布于斜率为1的直线附近,反射率的精度次之,一阶微分建模效果相对较差。
结合图7和图8对比发现,偏最小二乘回归模型的精度优于多元逐步回归模型,模型反演值更接近估测值。原因可能是单个波段的反射率难以全面反映不同LAI苔草的光谱信息,多元逐步回归模型只利用了几个波段的光谱信息,而偏最小二乘回归则从整个研究波段范围的光谱信息中提取主成分,保证相关性大的同时完成降维。因此,运用偏最小二乘回归方法对高光谱与苔草LAI进行回归分析,是研究苔草高光谱特征波段与苔草LAI关系很好的尝试。
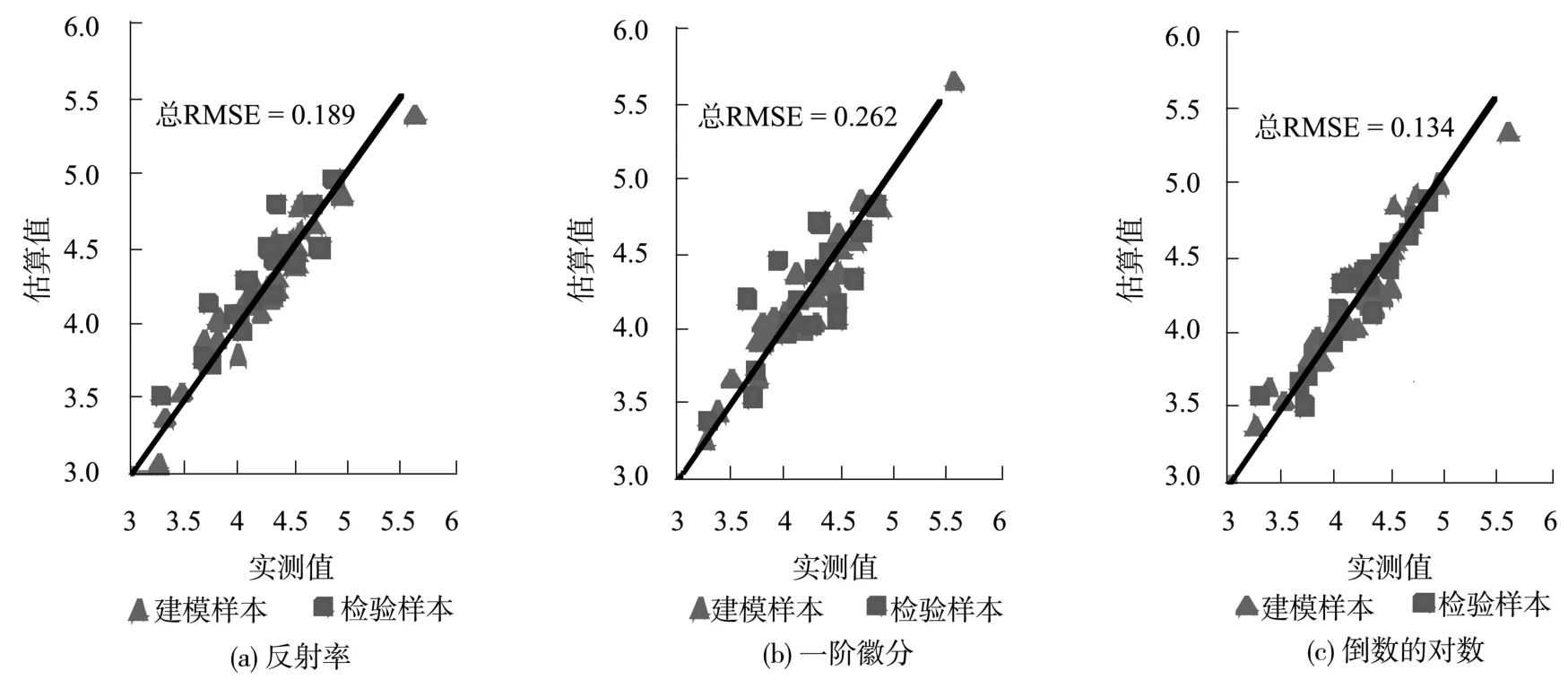
图8 苔草LAI偏最小二乘回归模型实测值与预测值的比较Fig.8 Comparison of measured Carex LAI and values estimated by PLSR model
3 结论与讨论
研究选用东洞庭湖苔草640~780 nm波段范围,在707~758 nm波段范围内,苔草反射率、一阶微分(R′)、倒数的对数log(1/R)与LAI均呈显著相关,选择特征波段并据此建立定量反演模型。结果表明:基于光谱反射率进行东洞庭湖苔草LAI估算研究可行;通过苔草光谱反射率进行数学变换,得到反射率的一阶微分及倒数的对数,有利于特征波段的选择。运用以上3种光谱数据与LAI进行多元逐步线性回归和偏最小二乘回归建模与分析,结果显示:多元逐步线性回归中一阶微分和倒数的对数表现较好,检验样本相对误差分别为5.603﹪、4.162﹪,估算值与实测值的相关系数分别为0.727、0.626,总体均方根误差分别为0.269、0.273;而在偏最小二乘回归中,反射率和倒数的对数精度较高,其检验样本相对误差分别为3.647﹪、2.679﹪,估算值与实测值的相关系数分别为0.812、0.894,总体均方根误差分别为0.189、0.134,建模决定系数均高达0.9以上,模型检验系数分别为0.812、0.894。基于光谱曲线特征波段进行的建模分析,并估算苔草的LAI,结果表明:偏最小二乘回归法优于多元线性逐步回归法。其中,反射率倒数的对数的偏最小二乘回归模型精度最高,检验样本估算的平均相对误差为2.679﹪,估算值和实测值的相关系数达到0.894,能较好快速估算苔草叶面积指数。因此,在样本容量小自变量多、变量间相关性较高时,偏最小二乘估计较多元线性逐步回归能更有效的提取和利用光谱中的重要信息。
值得指出的是,本研究的波段范围相对较窄,基于350~2 500 nm波长范围内建模与分析,本文的方法是否适用有待进一步探讨。此外,本文的方法是否适用于东洞庭湖的其它植被类型也有待深入研究。
[1] 杨 飞,张 柏,宋开山.大豆叶面积指数的高光谱估算方法比较[J].光谱学与光谱分析,2008,28(12):2951-2955.
[2] 陈沈斌. 种植业可持续发展的支持系统——农作物卫星遥感估产[J].地理科学进展,1998,17 (2):71-77.
[3] 王希群, 马履一, 贾忠奎, 等. 叶面积指数的研究和应用进展[J].生态学杂志,2005,24(5) : 537.
[4] Cliff H Koger. Wavelet analysis of hyperspectral reflectance data for detecting pittedmorningglory (Ipomoea lacunosa) in soybean(Glycine max) [J] .Ecology, 1969,50: 663-666.
[5] P.J. Zarco-Tejada. Hyperspectral indices and model simulation for chlorophyll estimation in open-canopy tree crops [J]. Remote Sensing of Environment ,2004,90: 463-476.
[6] Sonia Silvestri. Hyperspectral remote sensing of salt marsh vegetation,morphology and soil topography [J]. Physics and Chemistry of the Earth, 2003,28 :15-25 .
[7] 薛利红,曹卫星,罗卫红. 光谱植被指数与水稻叶面积指数相关性的研究[J].植物生态学报, 2004,28(1): 47-52 .
[8] 臧 卓,林 辉,杨敏华.ICA与PCA在高光谱数据降维分类中的对比研究[J].中南林业科技大学学报,2011,31,(11):18-22
[9] 刘秀英,臧 卓,孙 华.基于高光谱数据的杉木和马尾松识别研究[J].中南林业科技大学学报,2011,31,(11):30-33.
[10] 林 辉,刘 璇,臧 卓.杉木叶绿素含量高光谱遥感模型研究[J].中南林业科技大学学报.2010,30,(11):1-5.
[11] 刘伟东,项月琴,郑兰芬,等. 高光谱数据与水稻叶面积指数及叶绿素密度的相关分析[J].遥感学报,2000 , 4 (4) : 279-283.
[12] Patel NK, Patnaik C, Dutta J,et al. Hyperspectral versus multispectral data for estimating leaf area index in four different biomes [J]. International Journal of Remote Sensing, 2001,22:2401-2411.
[13] 王秀珍,王人潮,黄敬峰. 微分光谱遥感及其在水稻农学参数测定上的应用研究[J].农业工程学报, 2002,18(1):9-13.
[14] 刘 磊,沈润平,丁国香. 基于高光谱的土壤有机质含量估算研究[J].光谱学与光谱分析,2011,31(3):762-766.
[15] 刘焕军,张新乐,郑树峰. 黑土有机质含量野外高光谱预测模型[J].光谱学与光谱分析,2010, 30(12):3355-3358.
[16] 王秀珍, 黄敬峰, 李云梅, 等. 水稻叶面积指数的高光谱遥感估算模型[J].遥感学报, 2004 ,8 (1) : 81.
[17] 杨晓华,黄敬峰,王秀珍. 基于支持向量机的水稻叶面积指数高光谱估算模型研究[J].光谱学与光谱分析, 2008,28(8):1837-1841.
[18] 方秀琴,万 昌.叶面积指数(LAI)的遥感定量方法综述[J].国土资源遥感, 2003,3:58-62.
[19] 胡 昊,白由路,杨俐苹,等. 不同氮营养冬小麦冠层光谱红边特征分析[J].植物营养与肥料学报,2009,15(6):1317-1323.
[20] 蒋金豹,陈云浩,黄文江. 利用高光谱红边与黄边位置距离识别小麦条锈病[J].光谱学与光谱分析,2010;30(6):1614-1618.
[21] 卢艳丽,白由路,杨俐苹,等. 基于高光谱的土壤有机质含量预测模型的建立与评价[J].中国农业科学,2007 , 40 (9) :1898.
Studies on leaf area index estimation of Carex based on high-spectral data
QIU Lin, LIN Hui, SUN Hua, ZANG Zhuo, MO Deng-kui,
(Research Center of Forest Remote Sensing & Information Engineering , Central South University of Forestry &Technology , Changsha 410004, Hunan, China)
Leaf area index (LAI) is the important parameter for characterizing vegetation canopy structure and photosynthetic area size,as well as an important indicator to judge the status and trends of vegetation growth. Therefore, it is of great significance for monitoring the vegetation LAI real-time and dynamic. An optimal estimation model for the East Dongting Lake Carex LAI was designed by mathematical transformation of hyper-spectral data and feature analysis. Through analyzing the spectral reflectance and spectral signature of 52 Carex samples (bands ranging from 640 ~ 780 nm) which were collected from the east Dongtin lake, selecting characteristic bands,an estimation model was established by adopting multiple element step by step linear regression and partial least squares regression. The results show that the estimated characteristic band of the wavelength range were from 707~755 nm, the mathematical transformation of the spectral reflectance was good for the characteristic band bands choice; the SMLR model and PLSR model determination coefficient of the three types spectral data were 0.526, 0.815, 0.565, and the root mean square error were 0.320, 0.269, 0.273, while the PLSR model determination coefficient were all more than 0.9, the root mean square error were respectively 0.189, 0.262, 0.134. It is suggested that partial least squares regression method is better than stepwise multiple linear regression, it can estimate the LAI of Carex quickly and efficiently.
Carex; high-spectral data; vegetation types; leaf area index; reflectance; partial least squares regression method
S771.8
A
1673-923X (2012)07-0028-06
2012-04-18
国家重大专项(E0305/1112/02);国家“十二五”863项目(2012AA102001)
邱 琳(1988—),女,江西吉安人, 硕士研究生,研究方向:林业遥感和地理信息系统;E-mail:609556486@qq.com
林 辉(1965—),女,教授,博士生导师,主要从事林业遥感和地理信息系统的研究
[本文编校:欧阳钦]
——缺陷度的算法研究

