一类n－adic系统的混沌性

王立冬，于 旺，孙雪莲

(1.大连民族学院理学院，辽宁大连116605;2.辽宁师范大学数学学院，辽宁大连 116029)

一类n－adic系统的混沌性

王立冬1，于 旺2，孙雪莲1

(1.大连民族学院理学院，辽宁大连116605;2.辽宁师范大学数学学院，辽宁大连 116029)

引进了弱n－adic集映射和具有全n－adic集系统的概念，讨论了弱n－adic集映射具有正拓扑熵条件和具有全n－adic集系统在回复性上的混沌性。证明了n不是2的倍数的n－adic系统是Devaney混沌的，Wiggins混沌的，按序列分布混沌的，分布混沌的，Martelli’s混沌的，ω混沌的，Block and copple混沌的。

弱n－adic集;具有全n－adic集系统;混沌

自1975年Li和Yorke对于区间映射给出了混沌的严格数学定义(简称Li－Yorke混沌)以来，不同的学者从不同的角度给出了许多不同的混沌定义，而拓扑熵与各混沌之间的关系也成为了混沌研究的一个热门课题，人们发现，一个区间映射的正拓扑熵包含了 Li－Yorke混沌［1］，同时拓扑熵为零的区间映射是Li－Yorke混沌的例子被构造［2］。这说明区间映射的正拓扑熵是比Li－Yorke更强的结果。1994年，Schweizer和Smital扩展了Li－Yorke混沌的定义，并且证明了这个定义与区间映射的正拓扑熵是等价的，但当作用于更一般的空间映射时这个等价不再正确。在文献［3］中有一个含有正熵的映射，但没有DC1对的例子。

本文将通过n－adic系统进一步研究Devaney混沌的，Wiggins混沌的，按序列分布混沌的，分布混沌的，Martelli’s混沌的，ω混沌的，Kato’s混沌的，Block and copple混沌的，从而使我们进一步了解各种意义下的混沌。

1 基本概念与引理

定义1 设(X，d)是紧致度量空间，f:X→X是连续映射，如果存在集合D⊂X，使得对∀x，y∈D，x≠y有

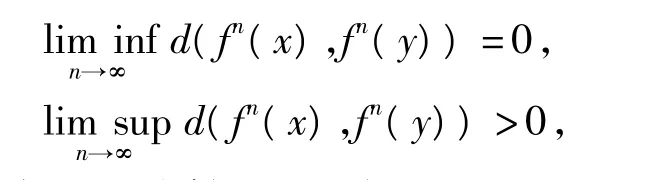
则称D是映射f的一个Li－Yorke混沌集;如果存在映射f的一个不可数的Li－Yorke混沌集，则称映射f是Li－Yorke混沌的，简称混沌的。

定义2设(X，d)是紧致的度量空间，称连续映射f:X→X是分布混沌的，如果存在不可数集D⊂X，使得对∀x，y∈D，x≠y 有

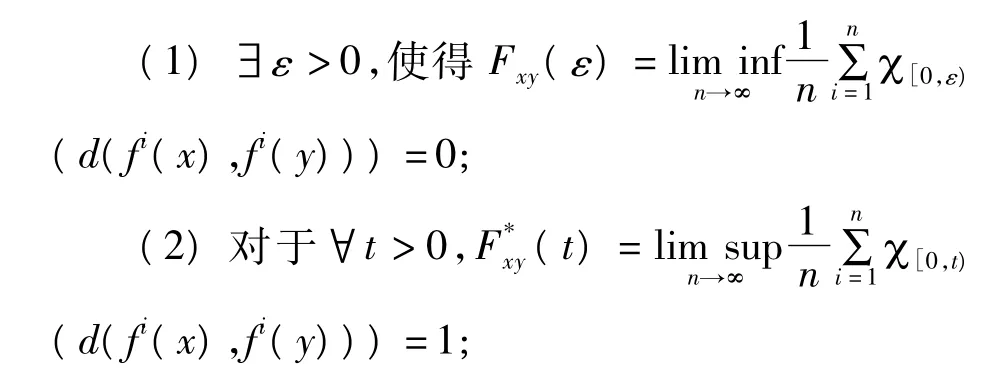
式中，χ［0，t)表示［0，t)上的特征函数，即 s∈［0，t)，χ［0，t)(s)=1，否则 χ［0，t)(s)=0;则称 D 为 f的分布混沌集，满足条件(1)(2)的两点x，y称为分布混沌点对。

定义3设(X，d)是紧致的度量空间，{pi}为严格递增正整数无穷序列，称连续映射f:X→X是按序列分布混沌的，如果存在不可数集D⊂X，使得对∀x，y∈D，x≠y 有

则称D为f按序列的{pi}分布混沌集，满足此定义中条件(1)和(2)的两点x，y称为按序列分布混沌点对。

定义4设(X，d)是紧致的度量空间，称连续映射f:X→X是Devaney混沌的，如果

(1)f是拓扑传递的;

(2)f的周期点在X中稠密;

(3)f具有对初值条件的敏感依赖性。

定义5设(X，d)是紧致的度量空间，称连续映射f:X→X为Martelli－混沌的，如果存在点x0∈X，使得

(1)ω(x0，f)=X;

(2)orb(x0)相对于X是不稳定的。

对于每个x∈X，点y∈X称为χ的ω极限点，如果序列f(x)，f2(x)，…，有一子序列趋近于y。x的ω 极限点记为 ω(x，f)。ω(x，f)中每个点称f为ω的极限点。

定义6 设X是一个度量空间，f:X→X是一个连续映射，称(X，f)是Wiggins－混沌，如果紧的不变子集Y⊂X满足:

(1)f|Y是拓扑传递的;

(2)f|Y是对初值敏感依赖的。

定义7称f是Block and Coppel混沌的，如果存在X的两个非交闭子集X0，X1和m∈N+满足:若 ~X=X0∪X1和 g=fm，则

(1)g=(~X)⊂~X;

(2)对于取值为0或1的每一个序列α=(α0，α1，α2，…)，存在点 x=xα∈~X 使得 gk(x)∈Xαk对∀k≥0 成立。

定义8称集合S⊂X(至少含两点)为ω稠密集，如果 S 满足对∀x，y∈S，x≠y 有

(1)ωf(x)ωf(y)是不可数的;

(2)ωf(x)∩ωf(y)是非空的;

(3)ωf(x)不包含在周期点里;

若存在不可数的ω稠密集S，则称映射f:X→X是ω混沌的。

定义9称不变闭集A⊂I是f的弱n－adic集，如果存在一个连续满射H:A→Z(n)使得对∀x∈A有τ◦H(x)=H◦f(x)，且当p=minA时对∀q∈A，q≠p有 H(p)≠H(q)。

定义10称不变闭集A⊂I是f的弱n－adic集，如果存在一个连续满射H:A→Z(n)使得对∀x∈A有τ°H(x)=H°f(x)，特别当A=I时称(Z(n)，τ)是具有全n－adic集的系统。

引理 1［4］若 ent(f)=0，x∈R(f) － P(f)且 f(x)＞χ，则对任意偶数m和奇数n有fm(x)＜fn(x)成立。

引理2［5］若f:I→I是连续的，则下列条件等价:

(1)ent(f)＞0;

(2)A(f)包含一个f的不可数混沌集;

(3)R(f)－A(f)包含f的不可数分布混沌集。

引理3［1］设 f:X→X，g:Y→Y 是连续的，其中X，Y是紧度量空间。若存在一个连续满射h:X→X 满足 g°h=h°f，则 h(A(f))=A(g)，h(R(f))=R(g)。

引理4［6］若f:I→I是连续的，则 ent(f)＞0当且仅当在Li－Yorke意义下Ω(f)中存在一个不可数的混沌集。

引理5［7］设f:I→I是一个区间映射，则 ent(f)＞0当且仅当存在一个闭不变子集Λ⊂I使得f|Λ在Devaney意义下是混沌的。

引理6［7］设f:I→I是一个区间映射，若 ent(f)＞0，则f在Wiggins意义下是混沌的。

引理7对于连续映射f:I→I，下列条件等价:

(i)f是拓扑混沌的，也就是说f有正的拓扑熵;

(ii)f是分布混沌的;

(iii)f是ω－混沌的;

(iv)f在Martelli意义下是混沌的;

(v)f在Devaney意义下是混沌的;

(vi)f在Block和Copple意义下是混沌的。

2 定理的证明

定理1若f有弱n－adic集且n不是2的方幂，则

(1)f│A(f)是分布混沌的;

(2)f│R(f)－A(f)是分布混沌的;

(3)f是ω混沌的;

(4)f是Devaney混沌的;

(5)f是Martelli混沌的;

(6)f是Block－Coppel混沌的;

(7)f是按序列分布混沌的;

(8)f是Winggins混沌的。

首先证明如果f有弱n－adic集且n不是2的方幂，则ent(f)＞0。

证明记n=k2m(k≥3且 k为奇数)，m≥0是整数。设A为f的弱n－adic集，则存在H:A→Z(n)的连续满射，使得对∀x∈A有τ°H(x)=H°f(x)，且当 p=minA时对∀q∈A，q≠p有 H(p)≠H(q)。

不失一般性，假定 H(p)=α=0α2α3…，令 V={z∈Z(n)|z1=0}，则V⊂Z(n)是α的开邻域，由H的连续性知存在ε＞0使得对∀q∈A，如果q－p＜ε则有H(q)∈V。因为当l→∞时τnl(α)→α，所以 fnl(p)→p。事实上由 τnl(α)→α(l→∞)可知 τnl(H(P))→H(P)(l→∞)，从而有H(fnl(p))→H(P)(l→∞)。下证 fnl(p)→p(l→∞)。

若fnl(p)不收敛于p，因{fnl(p)}是有界无穷点集，所以必有收敛子序列{f(nl)i(p)}。不妨设f(nl)i(p)→q≠p，从而 H(f(nl)i(p))→H(q)≠H(p)，这与H(f(n)i(p))→H(p)矛盾。故存在l≥0使得

令 g=f2lm，因为 τnl(α)→α，所以 H(fs(p))=τs(H(P))充要条件n是整除s。因为n不是2的方幂，所以n不能整除2lm，故H(f2lm(p))∉V，所以 g(p)=f2lm(p)－p≥q，从而 g(p)＞p。同理可证

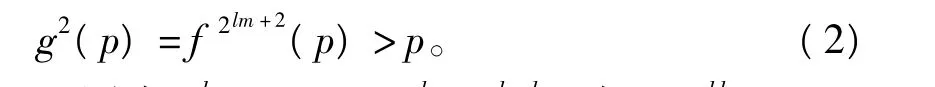
又因为nl=(k·2m)l=kl2lm，由于gkl(p)－p=fnl(p)－p，由式(1)知 gkl(p) －p＜ε，即 gkl(p)＜ε+p。由式(2)可得gkl(p)＜g2(p)。由于kl是奇数且p∈R(τ2lm)－p(τ2lm)，知 p∈R(g)－p(g)，又由引理1知ent(g)＞0，进一步可知ent(f)＞0。

由引理2可知，(1)(2)(7)成立;由引理7可知(3)(4)(5)(6)成立;由引理6可知(8)成立。

定理2若(Z(n)，τ)是具有全n－adic集系统且n不是2的方幂，则

(1)τ│A(τ)是分布混沌的;

(2)τ│R(τ)－A(τ)是分布混沌的;

(3)τ是Devaney混沌的;

(4)τ是Winggins混沌的;

(5)τ是Martelli混沌的。

(1)的证明因为(Z(n)，τ)是具有全nadic集系统，所以存在h:Z(n)→I的同胚映射使得对∀α∈Z(n)有 h°τ(α)=f°h(α)。根据推论1知f│A(f)是分布混沌的，再由引理3知对∀x∈A(f)存在一个α∈A(τ)使得h(α)=x。令D={α│α∈A(τ)，h(α)=x且 x∈A(f)}，则 D⊂A(τ)是一个不可数集，为了完成证明，只需说明D是τ的不可数分布混沌集即可。

首先，证明对于 ∀α1，α2∈D，如果对于某个t＞0 有 F(f，h(α1)，h(α2)，t)=0，则对某个 s＞0有 F(τ，α1，α2，s)=0。

因为τ:Z(n)→Z(n)，f:I→I是连续映射及h的一致连续性，所以存在一个s＞0使得对 ∀α1，α2∈A(τ) ，如果 ρ(α1，α2) ＜ s则有│h(α1) － h(α2)│ ＜ t。又因为 h°τi=fi°h，所以当 ρ(τi(α1)，τi(α2)) ＜s时有│hτi(α1) － hτi(α2)│ =│fi(h(α1)) －fi(h(α2))│ ＜t，这意味着对于任意的 n 有 ξn(τ，α1，α2，s)≤成立，再由 F 的定义ξn(f，h(α1)，h(α2)，t)可得

其次，证明如果对于∀s＞0 有 F*(f，h(α1)，h(α2)，s)=1，则对∀t＞ 0 有 F*(τ，α1，α2，t)=1成立。

因为是h同胚映射，所以存在逆映射h－1:I→Z(n)且是连续映射，再由第一步的证明，有ξn(f，h(α1)，h(α2)，s)≥ξn(τ，α1，α2，t)，进而有

由式(3)(4)和 α1，α2的任意性可得 D是 τ的一个不可数分布混沌集，即τ|A(τ)是分布混沌的。

同理可证(2)，根据定理1可知(3)(4)(5)成立。

［1］LIAO Gongfu，WANG Lidong.Almost periodicity china recurrence and chaos［J］.Israel.J.Math，1996，93，145－156.

［2］熊金成.线性映射的动力系统:非游荡点集，拓扑熵以及混乱［J］.数学进展，1988，17(1):5－6.

［3］SMITAL Jaroslav.Distribution chaos for triangular maps chaos［J］.Solitons Fractals21，2004，11:25 －28.

［4］ZBIGNIEW Nitecki.Maps of the interval with closed periodic set［J］.Proceeding of the American Mathematical Society，1982，85(3):451 －456.

［5］ LIAO Gongfu，WANG Lidong.Almost periodicity and the SS scrambled sets［J］.Chinese Annals of Mathematics，2002，23(6):685 －692.

［6］ZHOU Zuoling.Weakly almost periodic point and measure center［J］.Science in China(Ser.A)，1993，36:142－153.

［7］ SYLVIE Ruette，Chaos for continuous interval maps［EB/OL］.［2012 －03 －02］.http://www.math.upsud.fr/～ ruette/.

Chaotic Behavors for a Class of N－adic Systems

WANG Li－dong，YU Wang，SUN Xue－Lian
(1.College of Science，Dalian Nationalities University，Dalian Liaoning 116605，China;
2.School of Mathematics，Liaoning Normal University，Dalian Liaoning 116029，China)

In this paper，we introduce the map of weak n－adic systems set and the notion of a full n－adic set system.Then we discuss the condition of weak n－adic set map with positive topological entropy and the chaotic behavior of a full n－adic set system in the recovery.We prove that n －adic systems，in which n is not a power of 2，are Devaney chaotic，Wiggins chaotic，distributional chaos in a sequence，distributional chaos，Martelli’s chaotic，W － chaotic，Kato’s chaotic，Block and copple chaotic.

weak n－adic set;full n－adic set system;chaotic

O189

A

1009－315X(2012)05－0463－03

2012－03－02;最后

2012－03－29

国家自然科学基金项目(10971245);中央高校基本科研业务费专项资金资助项目(DC12010111，DC110311)。

王立冬(1955－)，男，吉林德惠人，教授，博士，特聘教授，博士研究生导师，主要从事拓扑动力系统研究。

(责任编辑 邹永红)