横观各向同性岩体位移解析解与数值解对比研究
李永涛,张志增,杨子胜,胡江春
(中原工学院,郑州450007)
横观各向同性岩体位移解析解与数值解对比研究
李永涛,张志增,杨子胜,胡江春
(中原工学院,郑州450007)
在横观各向同性岩体中巷道的位移解析解的基础上,运用数值计算软件FLAC3D,得到了不同倾角下的数值解,并将初始状态下的位移解析解同不同倾角下的数值解进行对比研究,通过误差分析得出了解析解的工程适用范围.
横观各向同性;解析解;数值解;工程适用范围
各向异性是岩体的一个重要性质,随着岩石力学理论和试验研究的不断深入,逐渐被人们所认识.由于分布有一组占绝对优势的结构面,层状岩体的变形和强度特性具有明显的各向异性,因此与各向同性岩体相比,其稳定性和破坏条件也表现得较为复杂,这对工程的施工及建筑物的稳定性会产生某些特殊的影响[1].各向异性使岩体的力学问题变得复杂,若将层状岩体当作各向同性岩体来进行工程设计和计算,将导致不可忽视的误差.对于层状岩体,一般在力学上可将其处理成横观各向同性岩体[2].所谓横观各向同性岩体,是指岩体在平行于层面的任意方向都具有相同的材料常数,而平行层面和垂直层面的材料参数则不同.
近年来,伴随着计算机技术的飞速发展,用于岩体稳定性分析的数值计算方法日臻成熟.当前应用于岩体工程问题的主要数值分析方法有:有限单元法、边界元法、有限差分法、离散单元法、无限元法、界面单元法、无单元法、非连续变形分析法、流形元法以及由以上各种方法相组合而得到的混合数值计算方法等.当岩体被裂隙切割成块体集合时,非连续的数值计算方法如离散单元法、非连续变形分析法等可以更逼真地反映岩体的内部结构,但块体的拓扑分析过于繁杂.所以目前在岩土工程的数值计算中,应用较广的还是基于连续介质力学的数值计算方法.
本文在横观各向同性岩体中巷道的位移解析解[3]的基础上,运用数值计算软件FLAC3D,得到了不同倾角下的数值解,并将初始状态下的位移解析解同不同倾角下的数值解进行对比研究.通过误差分析,首先得到了初始应力下的解析解的工程适用范围;然后改变水平初始地应力,验证了解析解的工程适用范围的适用性.
1 横观各向同性岩体中巷道的位移解析解
1.1 问题描述
对于圆形巷道,作如下假设:
(1)围岩为连续、均质、线弹性、横观各向同性岩体,位移和应变是微小的.
(2)巷道横断面平行于横观各向同性面,巷道横断面为圆形,a为巷道半径.
(3)巷道横断面尺寸远小于其轴向长度,因此,体积应变可以简化为平面应变进行求解.
(4)巷道埋深大于其半径的10倍,这种类型的巷道可以假设为深埋巷道.在巷道开挖前,巷道上部和下部位置的初始应力场是不等的.由于假设巷道为深埋,这种应力差可以忽略[4].
(5)初始地应力为二向不等压应力状态,竖直方向的初始地应力为p,水平方向的初始地应力为q.
(6)巷道围岩的自重相对于整个初始地应力来说较小,所以计算时可忽略影响范围内的自重.
这样就构成了二向不等压应力条件下横观各向同性岩体中圆形巷道的理想模型,如图1所示.
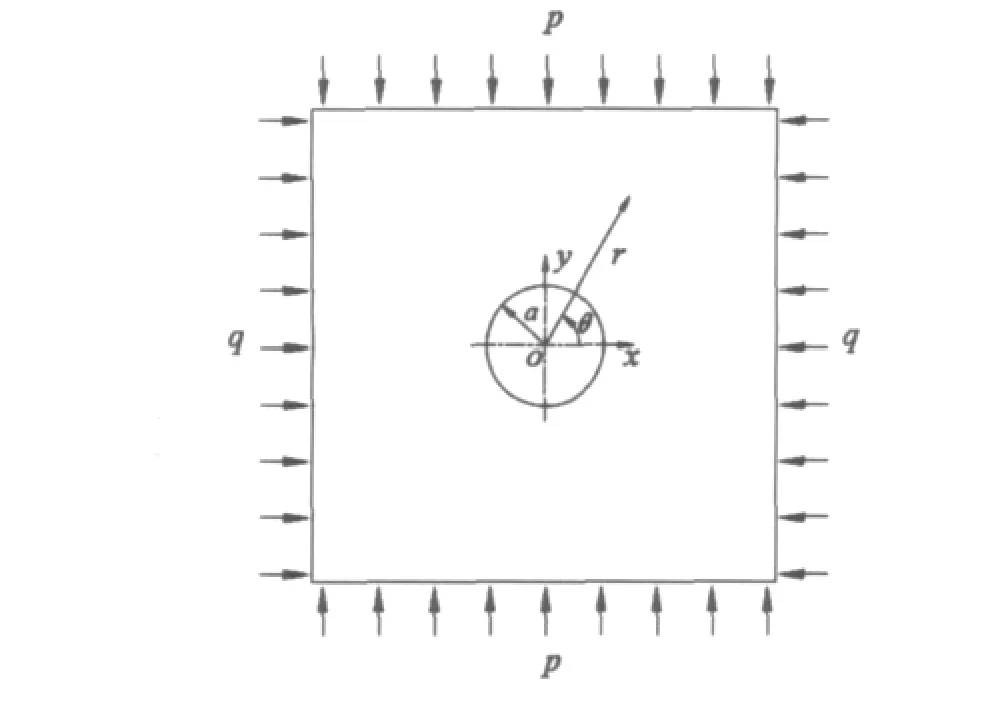
图1 横观各向同性岩体中圆形巷道的理想模型
1.2 横观各向同性岩体中圆形巷道的位移解析解
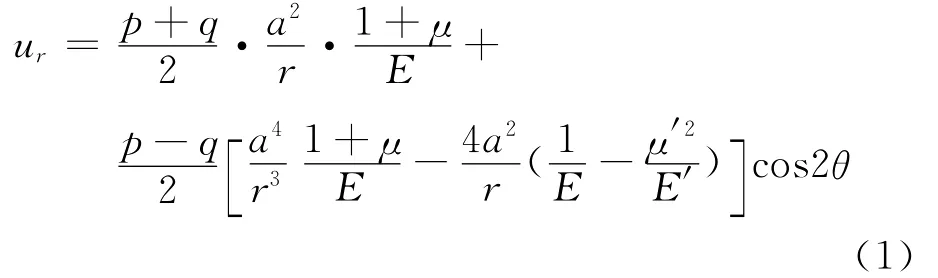
横观各向同性岩体中圆形巷道的位移公式[3]如下:式中:ur为横观各向同性岩体中圆形巷道的径向位移;E为横观各向同性面上的杨氏模量;μ为横观各向同性面上的泊松比;E′为垂直各向同性面上的杨氏模量;μ′为垂直各向同性面上的泊松比;r为极坐标下的半径;θ为极坐标下的倾角.
2 横观各向同性岩体中巷道的位移解析解与数值解的对比分析
2.1 p=10MPa,q=20MPa时位移解析解与数值解的对比分析
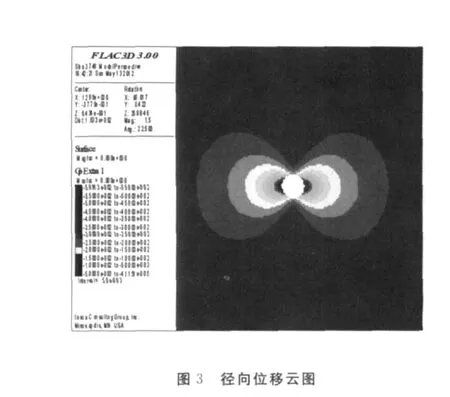
模型的计算区域为50m×50m,划分的网格见图2,其中xy平面为横观各向同性面.巷道的边界条件为:模型左侧和右侧限制水平方向移动,模型底部限制竖直方向移动.巷道半径α=2m;工程参数设为:p=10MPa,q=20MPa,E=1GPa,E′=0.8GPa,μ=0.25,μ′=0.3 .图3所示为计算得到的径向位移云图.此时,dd=0°,dip=0°(dd代表在xy 平面内测得的各向同性的倾向;dip代表在xy平面内测得的沿z轴负方向的各向同性平面的倾角).倾向与倾角是岩层产状3个要素中的2个要素(见图4).

岩层在空间的位置,称为岩层产状.倾斜岩层的产状,是用岩层层面的走向、倾向和倾角3个产状要素来表示的.
走向是岩层层面与水平面交线的方位角.岩层的走向表示岩层在空间延伸的方向.
倾向是垂直走向顺着倾斜面向下引出一条直线,此直线在水平面的投影的方位角.岩层的倾向,表示岩层在空间的倾斜方向.
倾角是岩层层面与水平面所夹的锐角.岩层的倾角表示岩层在空间倾斜角度的大小.
由于对称性,只在1/4的区域选取几个测点(见图5),然后将用FLAC3D计算得到的数值解与位移解析解进行对比分析.

图5 位移测点布置图
当p=10MPa,q=20MPa,dd=0°,倾角为5°、10°、15°、20°时,数值解与位移解析解见表1-表4(数值解与解析解的负号表示位移沿着径向指向开挖面).
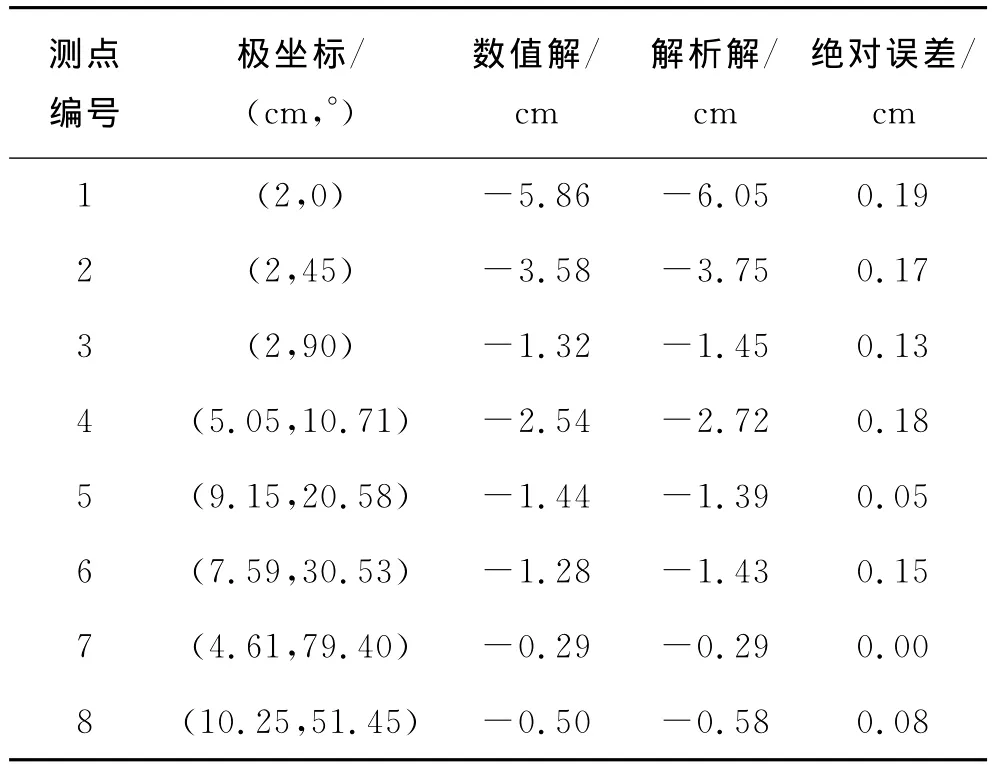
表1 倾角为5°时的数值解与解析解
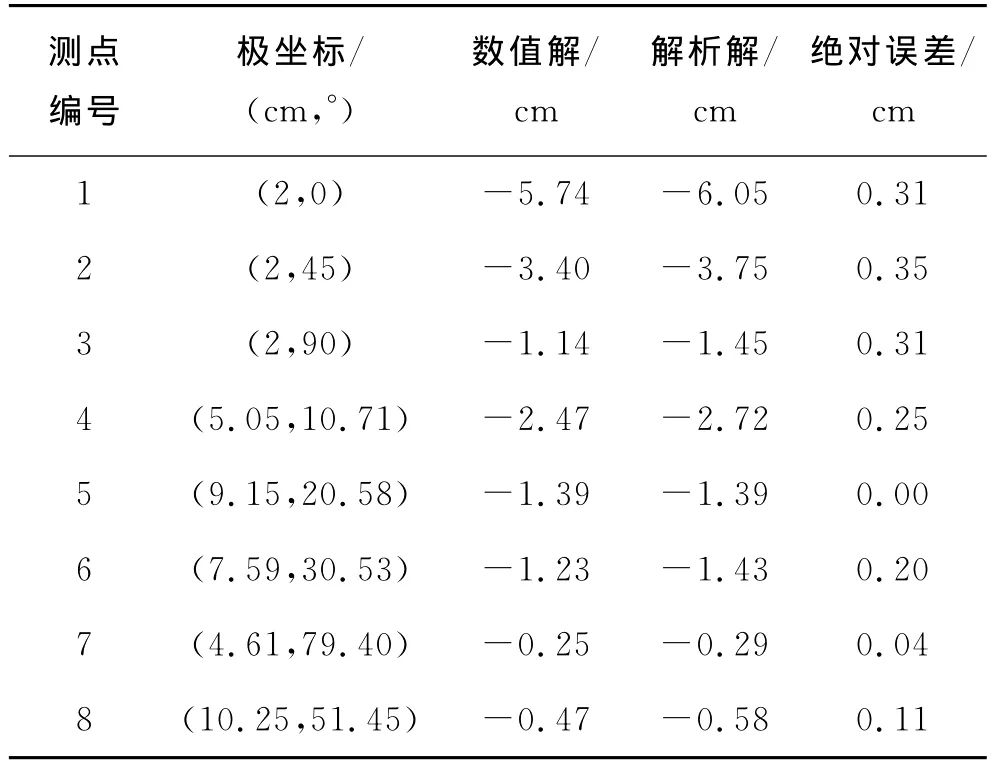
表2 倾角为10°时的数值解与解析解
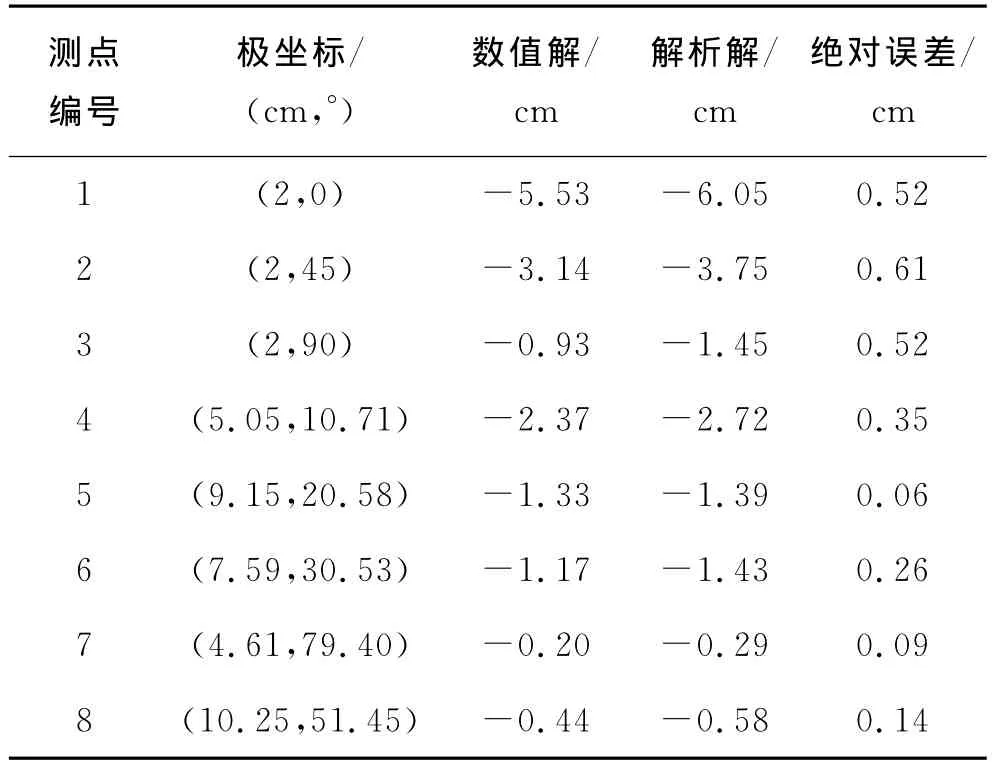
表3 倾角为15°时的数值解与解析解
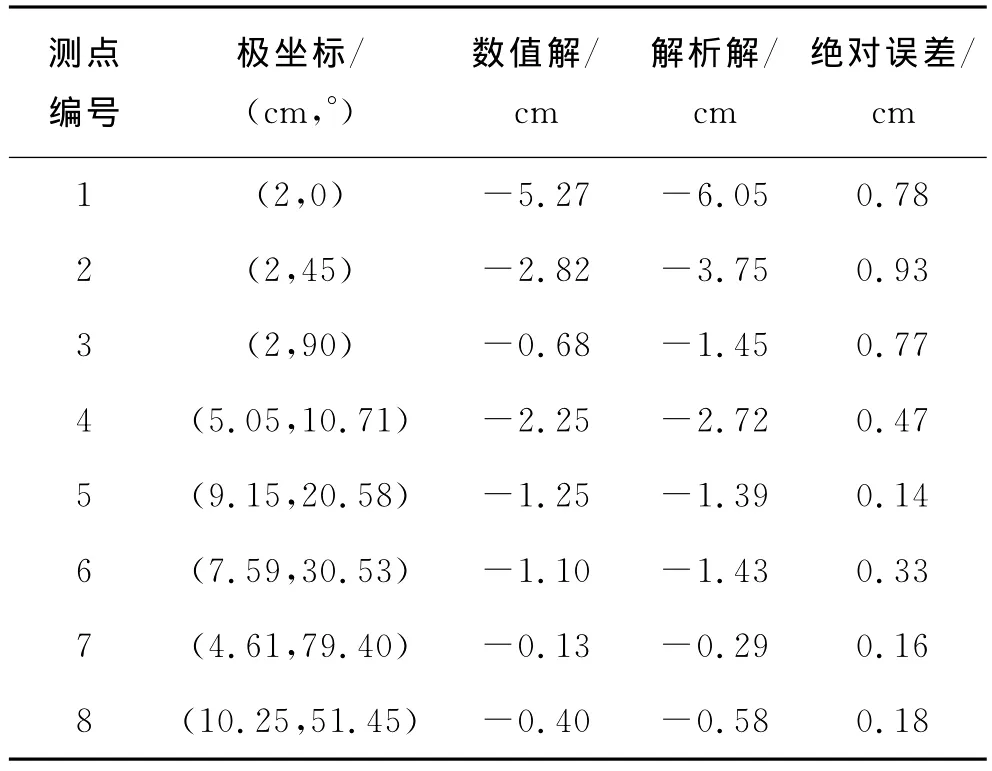
表4 倾角为20°时的数值解与解析解
根据模型计算区域的大小及实际工程的情况,本文将最大允许误差控制在0.50cm左右.由表1可以看出:当倾角为5°时,8个测点中的最大绝对误差(数值解与解析解之差的绝对值)为0.19cm,误差平均值为0.119cm.由表2可以看出:当倾角为10°时,8个测点中的最大绝对误差为0.35cm,误差平均值为0.196cm.由表3可以看出:当倾角为15°时,8个测点中的最大绝对误差为0.61cm,误差平均值为0.319cm,此时的最大绝对误差已经超出了允许范围,但误差平均值仍然在误差允许范围内.由表4可以看出:当倾角为20°时,8个测点中的最大绝对误差为0.93cm,误差平均值为0.470cm,此时的最大绝对误差已经远远超出了误差允许范围,误差平均值也接近误差允许范围.通过统计分析,将不同倾角下的误差均值做成曲线图,见图6.
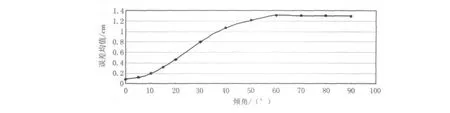
图6 误差均值曲线
对比分析不同倾角下的绝对误差值,并从图6所示的误差均值曲线可知:当倾角为20°时,误差平均值为0.470cm,最大绝对误差值为0.93cm,均方差为0.297cm;当倾角为15°时,误差平均值为0.319cm,最大绝对误差值为0.61cm,均方差为0.191cm.比较这2组数据可以看出:当倾角为20°时,由均方差反映的离散程度比倾角为15°时的离散程度大,且最大绝对误差值已经远远超出误差允许范围,误差平均值也非常接近误差允许范围,此时的解析解已经不适用.通过综合分析可以得出:在p=10MPa,q=20MPa,dd=0°,dip=0°的状态下,解析解的工程适用范围为倾角0°~15°.
2.2 改变水平初始地应力后位移解析解与数值解的对比分析
当p=10MPa,dd=0°,dip=15°,水平初始地应力分别为30MPa、80MPa时,数值解与位移解析解见表5和表6.
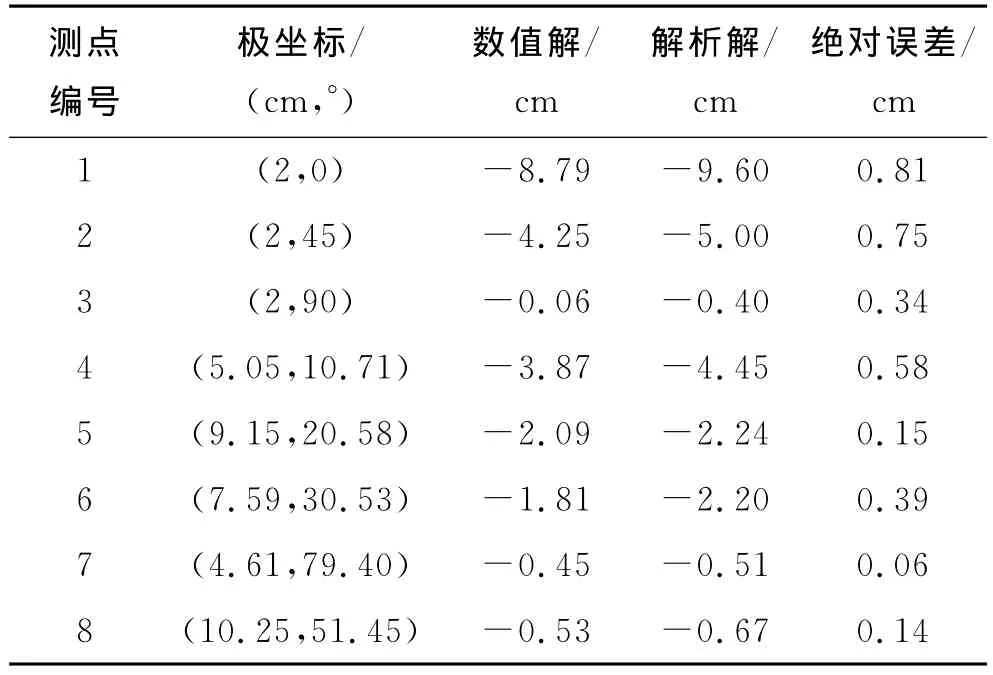
表5 水平初始地应力为30MPa时的数值解与解析解
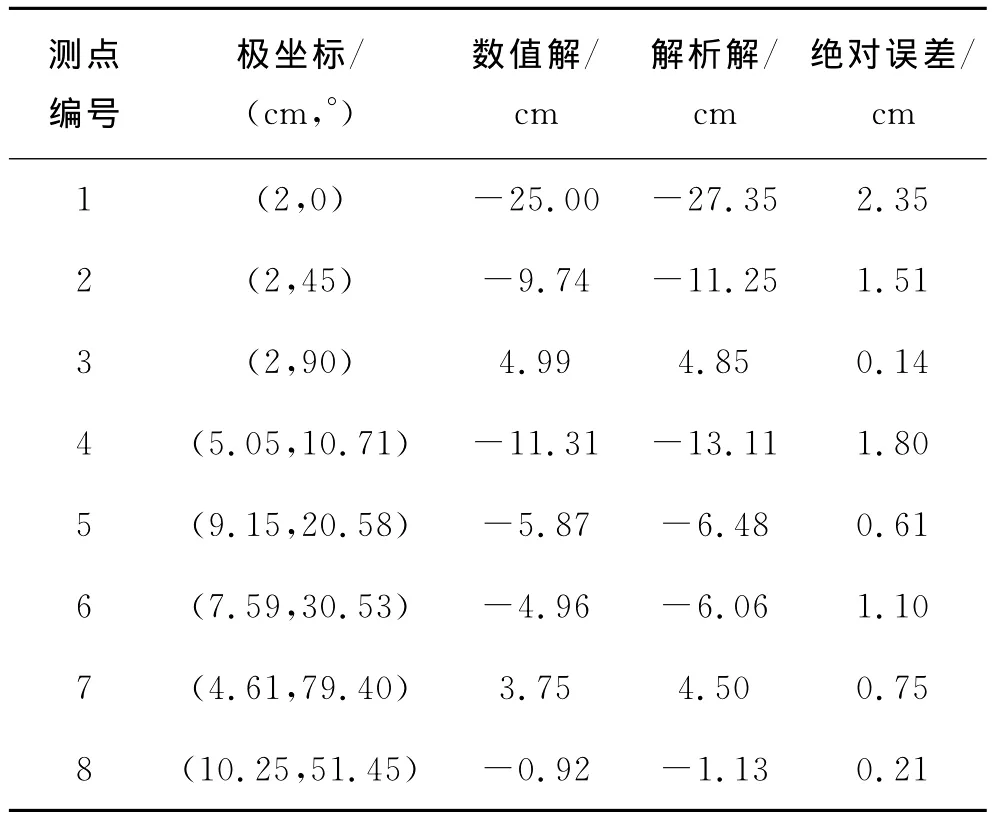
表6 水平初始地应力为80MPa时的数值解与解析解
改变水平初始地应力后,绝对误差就不能正确反映数据的对比情况,因此采用相对误差(绝对误差值与解析解的比值)进行分析.由表5可以得出,当水平初始地应力为30MPa、竖直方向初始地应力为10MPa、倾向为0°、倾角为15°时,相对误差为0.139;由表6可以得出,当水平初始地应力为80MPa、竖直方向初始地应力为10MPa、倾向为0°、倾角为15°时,相对误差为0.151.通过对比可知:当水平初始地应力改变幅度较大时,相对误差仍然保持相对稳定,即解析解的工程适用范围仍然适用.
将不同水平初始地应力下得到的位移解析解与数值解进行对比,经误差分析,得到p=10MPa,dd=0°,dip=15°,水平初始地应力为20~80MPa时的相对误差,见表7.

表7 相对误差
由表7可以看出:当水平初始地应力为20~80MPa时,相对误差基本控制在0.147左右,变化幅度基本不超过0.01,最大变化幅度也仅为0.012(接近0.01).因此,当水平初始地应力改变时,解析解的工程适用范围——倾角0°~15°仍然符合要求.
3 结 语
通过对横观各向同性岩体中巷道的解析解与数值解的对比研究,得出以下主要结论:
(1)在竖直初始地应力为10MPa、水平初始地应力为20MPa、倾向为水平面、倾角为0°的条件下,位移解析解的工程适用范围为倾角0°~15°.
(2)当水平初始地应力改变时,解析解的工程适用范围——倾角0°~15°仍然符合要求.
[1] Serrano A,Olalla C.Ultimate Bearing Capacity of an Anisotropic Discontinuous Rock Mass,Part I:Basic Modes of Failure[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1998,35(3):301-324.
[2] 张玉军,刘谊平.层状岩体抗剪强度的方向性及剪切破坏面的确定[J].岩土力学,2001,22(3):254-257.
[3] 张志增.横观各向同性岩体位移反分析的理论与应用研究[D].北京:清华大学,2010.
[4] 谭学术,鲜学福.复合岩体力学理论及其应用[M].北京:煤炭工业出版社,1994.
[5] 蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2002.
[6] 段靓靓,梁锴,方理刚.岩石横观各向同性参数试验研究[J].土工基础,2008,22(3):80-82.
[7] 彭文斌.FLAC3D实用教程[M].北京:机械工业出版社,2011.
The Comparative Study of Analytical Solutions and Numerical Solutions in Transversely Isotropic Rock
LI Yong-tao,ZHANG Zhi-zeng,YANG Zi-sheng,HU Jiang-chun
(Zhongyuan University of Technology,Zhengzhou 450007,China)
Based on the analytical solution of the roadway which is transversely isotropic rock mass in this paper,the numerical solution under different inclination by using of numerical software is gotten.Then a comparative study between the displacement solution in the initial state and the numerical solution with different inclination is done.The project scope of the analytical solution is gotten by deviation analysis.
transversely isotropic;analytical solution;numerical solution;project scope
TU471+.6
A
10.3969/j.issn.1671-6906.2012.05.011
1671-6906(2012)05-0046-05
2012-09-28
李永涛(1988-),男,河南新乡人,硕士生.

