基于集对分析的遥感图像K－均值聚类算法

谢相建，赵俊三，陈学辉，袁 思

(昆明理工大学国土资源工程学院，昆明 650093)

基于集对分析的遥感图像K－均值聚类算法

谢相建，赵俊三，陈学辉，袁 思

(昆明理工大学国土资源工程学院，昆明 650093)

基于欧式距离的K－均值聚类算法是一种硬分类(把每个待辨识的对象严格地划分到某个类中)方法，面对具有不确定性和混合像元特征的遥感图像数据，传统K－均值聚类算法很难得到满意的分类结果。为解决这一难题，将集对分析(set pair analysis，SPA)理论推广到遥感图像聚类算法，通过引入一个能统一描述同一性、差异性和对立性的同异反(identical discrepancy contrary，IDC)联系度，提出了基于IDC联系度的改进的K－均值聚类算法。该方法克服了传统K－均值算法硬分类的缺陷，可以有效地提高遥感图像聚类精度。对Landsat5 TM卫星数据的聚类分析实验表明，在含有混合像元的遥感图像地物覆盖分类中，改进的K－均值聚类方法的分类效果要优于传统K－均值聚类方法。

集对分析;K－均值聚类算法;同异反联系度;遥感图像

0 引言

遥感图像的分类根据分类过程中人工参与的程度可分为监督分类和非监督分类2大类。非监督分类也称为聚类分析或点群分析。聚类就是不需要人工选择训练样本，仅需极少的人工初始输入，计算机按一定规则自动地根据像元光谱或空间特征等组成集群簇，然后分类器将每个簇与参考数据比较，将其划分到某一类别中去［1］。在众多聚类算法中，K－均值聚类以其简单和高效的优点占据重要地位［2－4］，在遥感图像信息提取中也得到了广泛的应用［5－8］。K－均值聚类分析把每个待辨识的对象严格地划分到某个类中，是一种硬分类。而遥感图像信息的不确定性和混合像元问题使得对部分像元很难进行非此即彼的划分。事实上，遥感数据所反映的大多数地物覆盖在形态和类属方面都存在着中介性，没有明确的边界来区分它们。例如，荒裸地和稀疏草地的边界、城市和乡村的边界都是渐变的而且是非确定的。由 Dunn［9］提出、经 Bezdek［10］发展起来的模糊C均值(fuzzy C－means，FCM)聚类算法通过模糊隶属度得到样本属于各个类别的不确定性程度，表达了样本类属的中介性，即建立起了样本对于类别的不确定性的描述，能更客观地反映现实世界。然而，从表面上看，隶属度仅指明所研究对象属于给定参考集的程度，并没有指明所研究对象不属于给定参考集的程度以及属于还是不属于参考集的不确定程度，实质上是在给出这种隶属度的同时并没有指明这种隶属度的不确定性［11］。面对具有复杂对象不确定性特征的遥感图像分类，传统K－均值聚类算法很难得到满意的结果。为此，本文借助于集对分析(set pair analysis，SPA)的基本思想，从SPA的联系度入手，尝试引入一个能统一描述同一性、差异性和对立性的同异反［12］(identical discrepancy contrary，IDC)联系度 μ =a+bi+cj。IDC 联系度中的“同一度”a等价于模糊集理论中的隶属度;“对立度”c指明了所研究对象不属于给定参考集的程度;“差异度”b则指明了属于还是不属于参考集的不确定程度［11］;i，j分别表示差异度和对立度系数。通过用IDC距离替代K－均值中的欧式距离来度量像元之间的差异性，建立基于SPA的K－均值算法，使其能够对具有不确定性的遥感图像数据进行有效的聚类分析。以一景Landsat5 TM卫星图像数据为例，使用matlab模式分类工具箱进行聚类实验，并与传统K－均值算法聚类结果进行比较，验证基于SPA改进的K－均值聚类算法的有效性和优越性。

1 集对分析

SPA理论是我国学者赵克勤［12］于1989年提出的一种新型的处理模糊和不确定知识的系统理论和方法，该方法能够有效地分析和处理不精确、不一致、不完整等各种不确定信息，并从中发现隐含的知识，揭示潜在的规律。SPA从同一性、差异性和对立性3个方面研究2个事物的确定性与不确定性，全面刻画了2个不同事物的联系，是一种新的不确定性理论。其核心思想是认为任何系统都是由确定性和不确定性信息构成的，在这个系统中的确定性和不确定性可以相互联系、相互影响、相互制约，甚至在一定条件下相互转化，并借助于一个能充分体现上述思想的IDC联系度μ=a+bi+cj来统一地描述模糊、随机、中介和信息不完全所致的各种不确定性。

SPA的2个基本概念是“集对”及其“IDC联系度”。所谓集对，就是具有一定联系的2个集合所组成的“对”。设有联系的2个集合X和Y，它们各具有n个属性。可以组成一个集对 H(X，Y)，将X和Y的属性进行划分，如果其中s个属性是相同的，p个属性是相反的，f个属性既不相同又不相对立(称其为相异的)，则定义s/n为X和Y的同一度，f/n为X和Y的差异度，p/n为X和Y的对立度。用

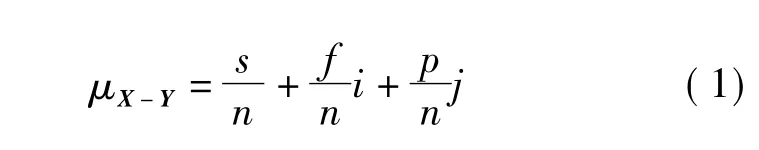
表示X和Y之间的关系，式中:i为差异度系数，i∈［－1，1］;j为对立度系数，一般恒取 j= －1;s+f+p=n; μX－Y为集对 H(X，Y)的 IDC 联系度。

记 a=s/n，b=f/n，c=p/n，则式(1)可写成

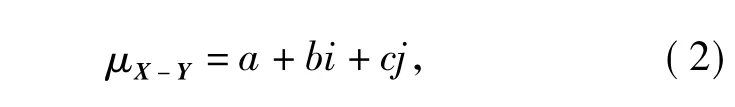
式中a，b，c为联系度分量，且满足a+b+c=1。

式(2)为常用的三元联系度表达式，其中a和c是相对确定的，而b是相对不确定的。这种相对性是由于客观对象的复杂性和可变性以及对客观对象认识与刻画的主观性和模糊性造成的不确定性，因而式(1)和式(2)是一种确定不确定结构函数，体现了确定不确定系统的对立统一关系，具有较深刻的方法论意义。当i和j取合理值时，式(1)和式(2)变为一个数值，称这个数值为联系数(记为μ')，根据联系度的定义有 μ'∈［－1，1］。

2 改进的K－均值聚类算法

2.1 K－均值聚类法

K－均值(K－means)算法是一种极为普遍和简单的基于划分的聚类算法，有着悠久的发展历史，曾被 Ball［13］，Lloyd［14］，MacQueen［15］和 Steinhaus［16］在各自不同的科学领域中提出。该算法的基本思想是:在n维欧几里得(Euclid)空间中把n个样本数据严格地分成K类。首先由用户确定所要聚类的准确数目K，并随机选择K个初始聚类中心;然后根据数据与中心的距离来将它赋给距离最近的类，重新计算每个类内对象的平均值形成新的聚类中心;反复迭代，直到所有类簇的误差平方和最小为止。

原始的K－均值聚类算法流程为:

设定输入数据集 X={x1，x2，…，xn}，最大循环次数I，聚类数目K;输出为 K个类簇 Cj，j=1，2，…，K。

步骤一，令I=1，随机选取K个数据点作为K个类簇的初始簇中心mj(I);

步骤二，计算每一个数据点xi与这K个簇中心的距离 d(xi，mj(I))，i=1，2，…，n;j=1，2，…，K;如果满足 d(xi，mj(I))=min{d(xi，mj(I))，j=1，2，…，K}，则 xi∈Cj;

步骤三，重新分配K个新的聚类中心，即

步骤四，计算目标函数J(C)，即

若目标函数J(C)取得最小，则返回mj(I)，k=1，2，…，K，算法结束;否则I=I+1，返回步骤二。

2.2 基于SPA改进的K－均值聚类方法

把SPA理论引入K－均值算法［17］，形成基于IDC距离的K－均值算法，其基本思想是:将待分类样本 xl(l=1，2，…，n)和聚类中心 mk(k=1，2，…，K)都看做是具有T个属性的集合X和M。首先，分别将待分类样本xl与聚类中心mk组成集对H(X，M)，得到对应于第t个属性的IDC联系度，即

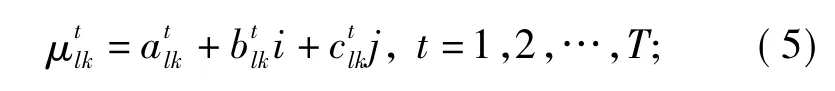
然后计算待分类样本xl与聚类中心mk的IDC距离Dlk，即

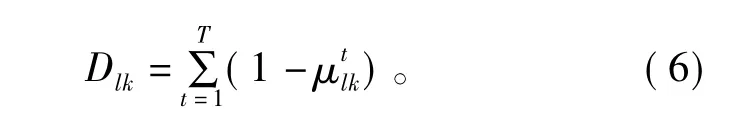
比较样本xl与各聚类中心mk之间的IDC距离Dlk的大小，若 Dl=min{Dlk，k=1，2，…，K}，则认为第l个样本xl与第k个聚类中心mk最接近，故将xl归入簇类k(此即IDC模式识别的择近原则)。

该算法的具体实现步骤如下:

设定输入数据集 X={x1，x2，…，xn}，聚类簇个数K，差异度系数i，最大循环次数I;输出为满足“误差平方和最小”标准的K个聚类Ck。

步骤一，初始化。令I=1，随机选取K个初始类簇中心 mk(I)，k=1，2，…，K;

步骤二，计算IDC联系度。计算待分类样本xl与聚类中心mk的IDC联系度μlk;

步骤三，分配xl。计算样本点xl与这K个簇中心之间的 IDC距离 Dlk，如果满足 Dlk=min{Dlk，k=1，2，…，K}，则 xl∈Ck;

步骤四，修正簇中心Ck。令I=I+1，重新分配K个新的聚类中心，即

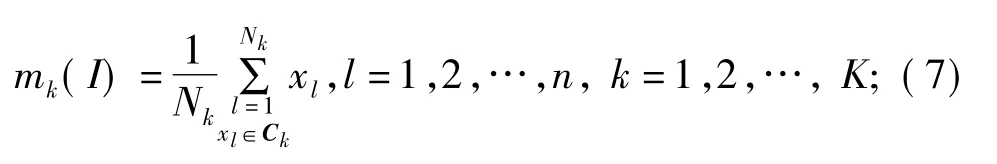
步骤五，计算误差平方和J，即

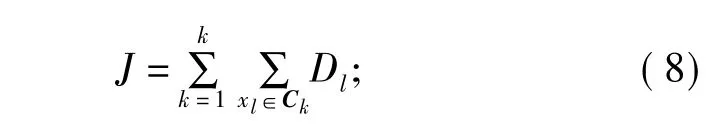
步骤六，收敛判断。如果J值收敛，则返回mk(I)，k=1，2，…，K;算法结束;否则，返回步骤二。

3 实验与结果分析

为了评价改进算法的聚类性能，选取一景多光谱遥感图像作为实验数据，并与传统K－均值算法进行比较。全部实验均使用MATLAB 7.11在AMD Athlon642.20 GHz、内存为2G 的 Windows XP操作系统上进行。

实验区为曲靖市陆良县地区，实验数据为2006年5月19日获取的Landsat5 TM卫星图像。TM图像包含7个波段，图像大小为400像元×400像元。参照文献［18］，针对实验区的特点，结合2006年曲靖市土地覆盖利用状况调查，确定聚类结果的类别组成如表1。

表1 实验区土地覆盖利用类别Tab.1 Classes of the land cover in the test area

实验区内各类地物错综分布，较为复杂。为便于更好地对地物进行目视识别和聚类效果比较，将原始TM图像按TM4(R)，TM3(G)和TM2(B)组合进行假彩色合成(图1，其中黑色椭圆附近为植被稀疏地，白色矩形框附近为建筑用地)。

图1 TM4(R)，TM3(G)，TM2(B)假彩色合成图像Fig.1 False color image composed with TM4(R)，TM3(G)and TM2(B)

以TM图像的TM1—TM5，TM7六个波段数据为分类对象，分别采用传统K－均值算法和基于SPA改进的K－均值算法对其进行聚类，聚类簇个数K=6。

对改进算法中样本像元与聚类中心之间各波段的IDC联系度分量进行计算。其中，同一度为

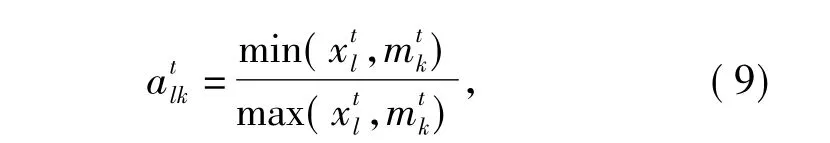
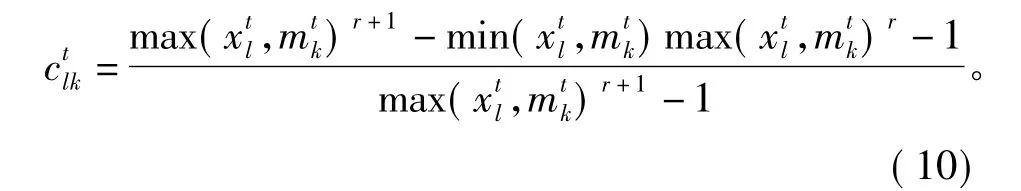
根据SPA理论，式(2)必须满足a+b+c=1，得到对应的差异度，即

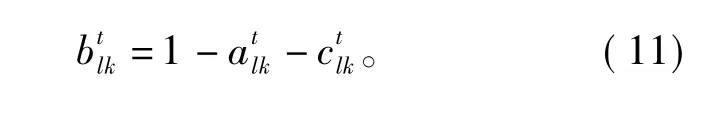
最后由式(5)—(6)计算出满足“误差平方和最小”标准的K个聚类Ck。采用传统K－均值算法的聚类结果如图2(a)所示，基于SPA改进的K－均值算法(r=1.63，i=0.5)聚类结果如图 2(b)所示。

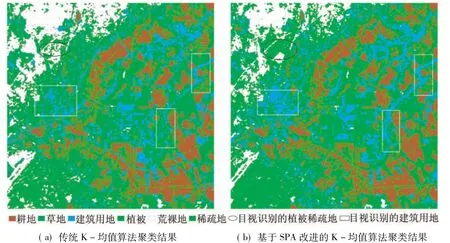
图2 传统与改进K－均值算法聚类结果对比Fig.2 Comparison between clustering results of traditional and improved K －means algorithm

以实际土地覆盖/土地利用状况调查为基础，对照TM假彩色合成图像进行的验证，并在图像上均匀选取约6000个像元，判读出其类别，作为实验数据的地面实况(ground truth);然后在相同的位置上，分别读出采用传统K－均值聚类方法和改进的K－均值聚类方法结果图上的类别。分类精度的评价指标以分类后的混淆矩阵为基础，分别计算制图精度、用户精度、总体分类精度和Kappa系数［1］，与地面实况数据对比后，两种算法分类结果见表2和表3。

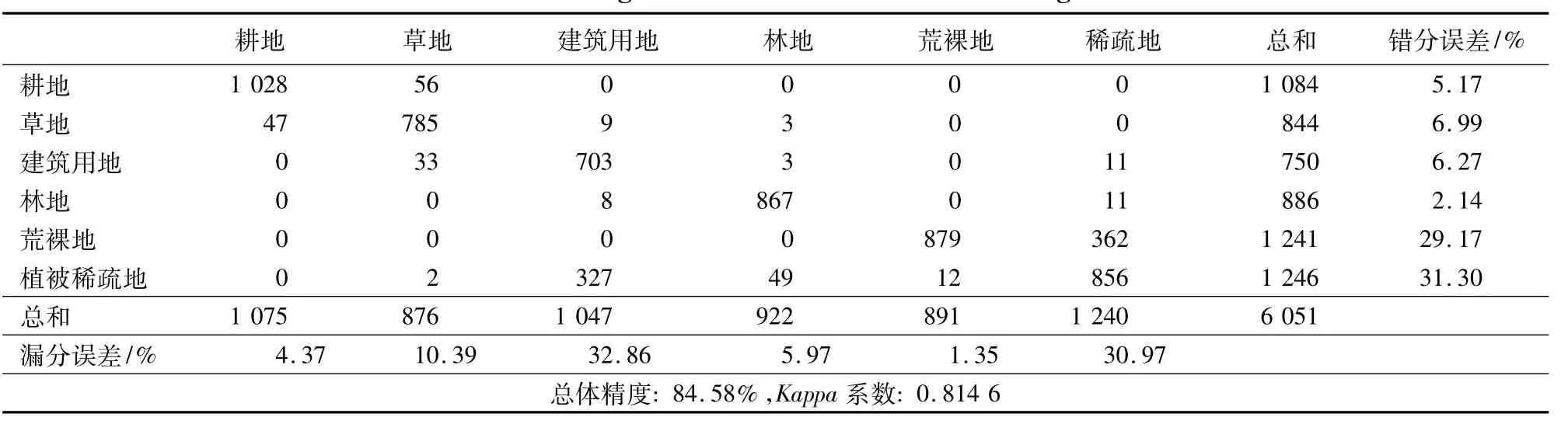
表2 传统K－均值算法聚类结果Tab.2 Clustering result of traditional K －means algorithm

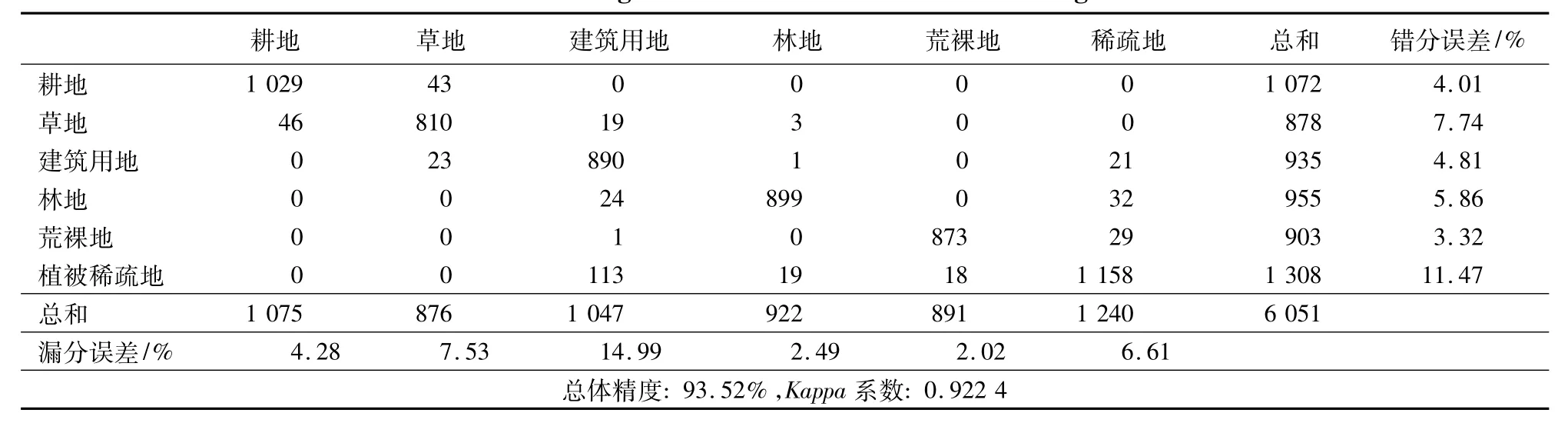
表3 基于SPA改进的K－均值算法聚类结果Tab.3 Clustering result of SPA －based K －means algorithm

通过比较可以看出，与传统K－均值聚类方法相比，利用基于SPA改进的K－均值聚类方法对含混合地物的土地覆盖能得到更精确的划分。比如，通过对比图1和图2(a)可以很清晰地看出，传统K－均值算法把图1中黑色椭圆附近的植被稀疏地错分成了荒裸地;而在图2(b)中改进的K－均值算法很清楚地将植被稀疏地与荒裸地划分开来。同时，图1中白色矩形框附近的部分建筑用地，在图2(a)中被错分成了植被稀疏地，而在图2(b)中基于SPA改进的K－均值算法却对建筑用地实现了较好的划分。从表2和表3中2种分类算法结果比较也可以看出，对于建筑用地、植被稀疏地、草地和林地的错分、漏分误差，基于SPA的改进算法要低于传统K－均值算法;对于总体分类精度和Kappa系数，基于SPA的改进算法明显高于传统K－均值算法。

4 结论

1)由于遥感研究对象特征的不确定性和混合像元问题，以欧式距离为度量函数的传统K－均值聚类算法，在遥感图像分类中很难得到满意的结果。本文将集对分析(SPA)方法应用于K－均值聚类，提出了一种基于SPA改进的K－均值聚类方法。

2)改进的K－均值聚类方法利用同异反(IDC)联系度来度量样本间的相似性，尝试解决传统K－均值算法在含有混合像元的遥感图像地物覆盖分类中由硬分类造成分类精度不高的问题。实验结果显示，在传统K－均值聚类算法面对具复杂特征的遥感图像数据无法获得较好聚类效果时，基于SPA改进的K－均值聚类算法仍然能够获得较好的聚类效果。

［1］赵英时，陈冬梅，杨立明，等.遥感应用分析原理与方法［M］.北京:科学出版社，2003.Zhao Y S，Chen D M，Yang L M，et al.Principles and Methods of Remote Sensing Applications［M］.Beijing:Science Press，2003(in Chinese).

［2］Huang Z X.Extensions to the K －means Algorithm for Clustering Large Data Sets with Categorical Values［J］.Data Ming and Knowledge Discovery，1998，2(3):283 －297.

［3］Kaufman L，Rousseeuw P J.Finding Groups in Data:An Introduction to Cluster Analysis［M］.Beijing:Wiley Online Library，1990.

［4］Hansen P，Jaumard B.Cluster Analysis and Mathematical Programming［J］.Math Program，1997，79(1/3):191 － 215.

［5］邓湘金，王彦平，彭海良.高分辨率遥感图像的聚类［J］.电子与信息学报，2003，25(8):1073 －1080.Deng X J，Wang Y P，Peng H L.The Clustering of High Resolution of Remote Sensing Imagery［J］.Journal of Electrics and Information Technology，2003，25(8):1073 －1080(in Chinese with English Abstract).

［6］钟燕飞，张良培.遥感影像K均值聚类中的初始化方法［J］.系统工程与电子技术，2010，32(9):2009 －2014.Zhong Y F，Zhang L P.Initialization Methods for Remote Sensing Image Clustering Using K － means Algorithm［J］.Journal of System Engineering and Electronics，2010，32(9):2009 －2014(in Chinese with English Abstract).

［7］刘小芳，何彬彬，李小文.基于半监督核模糊c－均值算法的北京一号小卫星多光谱图像分类［J］.测绘学报，2011，40(3):301－306.Liu X F，He B B，Li X W.Classification for Beijing－1 Microsatellite’s Multispectral Image Based on Semi－ supervised Kernel FCM Algorithm［J］.Acta Geodaetica et Cartographica Sinica，2011，40(3):301 －306(in Chinese with English Abstract).

［8］哈斯巴干，马建文，李启青，等.模糊C－均值算法改进及其对卫星遥感数据聚类的对比［J］.计算机工程，2004，30(11):14－15.Hasi B G，Ma J W，Li Q Q，et al.Improved Fuzzy C － mean Classifier and Comparison Study of Its Clustering Results of Satellite Remotely Sensed Data［J］.Computer Engineering，2004，30(11):14－15(in Chinese with English Abstract).

［9］Dunn J C.A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well Separated Cluster［J］.Cybernetics and Systems，1974，3:32 －57.

［10］Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithms［M］.New York:Plenum Press，1981.

［11］赵克勤.集对分析的不确定性系统理论在AI中的应用［J］.智能系统学报，2006，1(2):16 －25.Zhao K Q.The Application of Uncertainty Systems Theory of Set pair Analysis(SPA)in the Artificial Intelligence［J］.CAAI Transactions on Intelligent Systems，2006，1(2):16 － 25(in Chinese with English Abstract).

［12］赵克勤.集对分析及其初步应用［M］.杭州:浙江科学技术出版社，2000.Zhao K Q.Set Pair Analysis and Its Preliminary Application［M］.Hang Zhou:Zhejiang Science and Technology Press，2000(in Chinese).

［13］Ball G H.ISODATA，a Novel Method of Data Analysis and Pattern Classification［R］.Menlo Park:DTIC Document，1965.

［14］Lloyd S.Least Squares Quantization in PCM［J］.IEEE Transactions on Information Theory，1982，28(2):129 －137.

［15］MacQueen J.Some Methods for Classification and Analysis of Multivariate Observations［C］//In:Fifth Berkeley Symosium on Mathematics.Statistics and Probability.California:University of California Press，1967:281 －297.

［16］Steinhaus H.Sur la Division Des Corp Materiels en Parties［J］.Bull Acad Polon Sci，1956，4(1):801 －804.

［17］赵克勤.基于集对分析的对立分类、度量及应用［J］.科学技术与辩证法，1994，11(2):26 －30.Zhao K Q.The Classification，Measurement and Applications Based on Set Pair Analysis［J］.Science，Technology and Dialectics，1994，11(2):26 －30(in Chinese with English Abstract).

［18］中华人民共和国质量监督检验检疫总局和中国国家标准化管理委员.GB/T 21010－2007土地利用现状分类［S］.北京:中国标准出版社，2007.Standardization Administration and GeneralAdministration of Quality Supervision，Inspection and Quarantine of the People’s Republic of China.GB/T 21010 －2007 The Classification of Current Land Use［S］.Beijing:China Standards Publishing House，2007(in Chinese).

SPA－based K－means Clustering Algorithm for Remote Sensing Image

XIE Xiang－jian，ZHAO Jun－san，CHEN Xue－hui，YUAN Si
(Faculty of Land and Resource Engineering，Kunming University of Science and Technology，Kunming 650093，China)

K－means clustering algorithm is a kind of hard classification based on the Euclidean distance，with each data point assigned to a single cluster.Due to the uncertainty and mixed pixels in remote sensing image，it is difficult for the traditional K －means clustering algorithm to obtain satisfactory classification results.To overcome this drawback，the authors applied the SPA(set pair analysis)theory to the clustering algorithm of remote sensing image.The IDC(identical discrepancy contrary)connection degree model，which can descript unitarily the identity，discrepancy and opposition，was employed to improve K －means clustering algorithm.The improved algorithm has overcome the limitation of K －means clustering algorithm to certain extent.Clustering analysis experiments of Landsat TM image show that the improved K－means clustering algorithm is superior to K－means in classification accuracy of ground cover class components of mixed pixels.

set pair analysis(SPA);K－means clustering algorithm;identical discrepancy contrary(IDC)connection degree;remote sensing image

TP 751.1

A

1001－070X(2012)04－0082－06

2011－12－29;

2012－02－09

国家自然科学基金“面向对象的土地利用空间多尺度耦合机理研究”(编号:41161062)资助。

10.6046/gtzyyg.2012.04.14

谢相建(1987－)，男，硕士研究生，主要从事遥感图像处理方面的研究。E－mail:xiexjrs@gmail.com。

(责任编辑:刘心季)