用劈窗算法反演地表温度的通道问题讨论
孟 鹏,胡 勇,巩彩兰,栗 琳
(1.中国科学院上海技术物理研究所,上海 200083;2.中国科学院研究生院,北京 100049)
用劈窗算法反演地表温度的通道问题讨论
孟 鹏1,2,胡 勇1,巩彩兰1,栗 琳1,2
(1.中国科学院上海技术物理研究所,上海 200083;2.中国科学院研究生院,北京 100049)
劈窗算法是基于热红外遥感数据反演地表温度中应用较为广泛、且简单有效的算法之一,所使用的热红外通道主要位于10~13.3 μm(1000~750 cm-1)波长区间内,很少考虑8 ~9.09 μm(1250 ~1100 cm-1)区间内的通道数据。为了探讨更多的适合于反演地表温度的通道数据,结合劈窗算法基本公式的推导过程,归纳出了与通道设置相关的问题,并针对这些问题在10 ~13.3 μm(1000 ~750 cm-1)和8 ~9.09 μm(1250 ~1100 cm-1)区间内进行了数值模拟分析。结果显示,用基于此推导劈窗算法,通过迭代求解,利用8~9.09 μm(1250~1100 cm-1)和10~13.3 μm(1000~750 cm-1)波长区间内数据进行温度反演的结果非常接近,因此认为,将 8 ~9.09 μm(1250 ~1100 cm-1)波长区间内的数据用于劈窗算法反演地表温度具有一定的可行性。
劈窗算法;地表温度;热红外通道;MODTRAN
0 引言
地球表面温度是一项重要的地球物理参数。人们希望获得不同空间分辨率、任意覆盖和多时相的地表温度数据,为此,遥感应用工作者提出了一系列用热红外遥感数据反演地表温度的算法,如:针对只有1个热红外通道数据(TM/ETM+6)的单通道算法[1,2]、针对具有 2 个热红外通道数据(NOAA/AVHRR)的劈窗算法[3]、针对具有5个热红外通道数据(Terra/ASTER)的温度发射率分离算法(TES)[4]以及针对 7个红外通道数据(Terra/MODIS)的昼夜算法[5],等等。单通道算法是基于大气校正的温度反演方法,计算复杂且误差较大;TES算法和MODIS昼/夜算法虽然也具有一定的优势,但需要多个热红外通道数据,且计算复杂度较高,因而其应用受到一定的限制。与单通道和多通道算法相比,针对2个热红外通道数据的劈窗算法计算简单、方法成熟,是目前应用最为广泛的温度反演算法之一。
当前劈窗算法所使用的通道主要位于10~13.3 μm(1000 ~750 cm-1)波长区间内,很少涉及8~9.09 μm(1250 ~1100 cm-1)区间内的热红外通道。从遥感探测器的设计角度考虑,研制用于10 μm内长波红外探测的长线列或面阵器件的技术成熟度要高,所以在此基础上进行10 μm内的热红外通道遥感应用分析就显得比较有意义。本文的研究目标就是对8~9.09 μm(1250 ~1100 cm-1)区间内的热红外通道用于劈窗算法进行地球表面温度反演的可行性进行分析。
1 热红外辐射传输基本理论
1.1 Planck 函数
1900年,Planck用量子物理的新概念补充了经典物理理论,给出了可以准确表达黑体热红外辐射能量的Planck函数[6]。以波数v(波长的倒数)表示黑体的分光辐射亮度[7],其表达式为

式中:B(v,T)代表黑体的分光辐射亮度,W·cm-2·sr-1·cm;h为普朗克常量,h=6.6252×10-34J·s;k 是玻尔兹曼常量,k=1.38044 ×10-23J·K-1;c是光速,c=2.997925 ×108m·s-1;T 为热力学温度,K。
1.2 热红外辐射传输方程
Chandrasekhar[8]把传感器接收的热红外辐射表达为地物辐射、大气的上行辐射和大气下行辐射经地表反射辐射3项之和。热红外辐射传输方程的建立主要从大气透过情况、大气上下行辐射、观测时卫星天顶角、视场内目标的复杂度和探测器的通道响应等多方面进行考虑。
2 劈窗算法的推导
为了探讨将8 ~9.09 μm(1250 ~1100 cm-1)区间内的数据用于劈窗算法进行地球表面温度反演的可行性,同时降低分析的难度和保证准确度,选择发射率均一且辐射特性接近黑体的海洋表面作为研究对象,忽略大气下行辐射的影响。
Mcminllin[9]假定海洋表面发射率为 1,天空晴好,并且在忽略多次散射的条件下,给出了热红外辐射传输方程表达式为

式中:I(v,T)表示大气顶层辐射亮度;v表示波数;T表示亮度温度;B是普朗克分光辐射亮度;Ts是地球表面温度;τ是透过率;T(P)表示大气压强为P时的大气温度;P0是地球表面压强;θ是卫星天顶角。根据积分中值定理,有
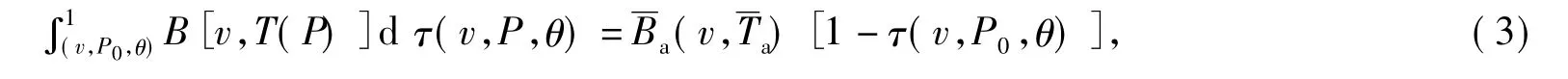

式中:I(v,T),B(v,Ts)和均为含普朗克函数项。假定在一定的波谱范围内,可以对普朗克函数项进行泰勒级数一阶展开,整理后得到
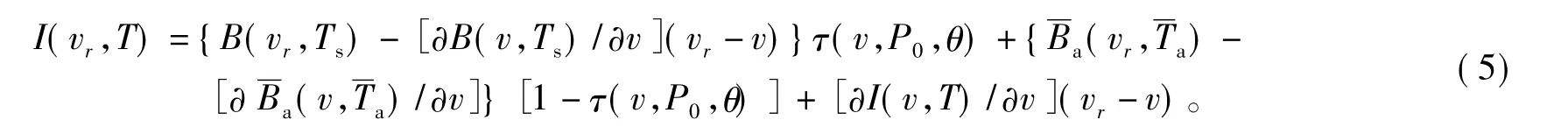
若存在

则式(5)变为
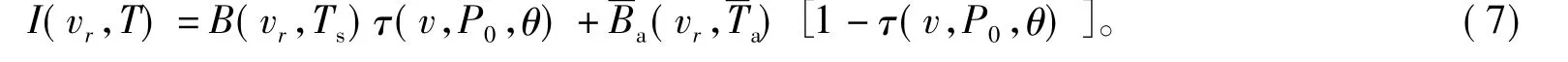
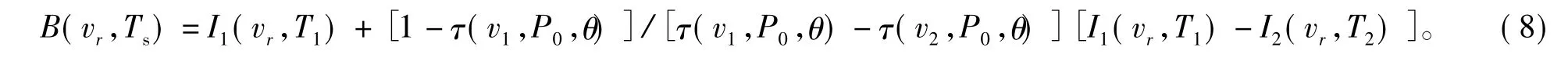
令
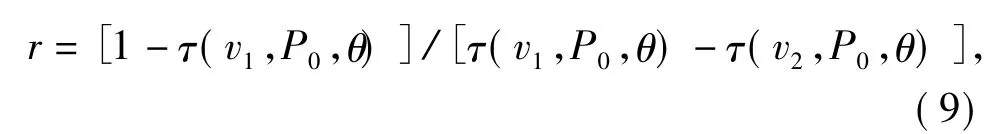
则有

式中:I1(vr,T1),I2(vr,T2)分别为 2 个通道的光谱辐射亮度;γ为和大气状态紧密相关的量。若γ值确定,则可以确定B(v,Ts),从而计算出Ts。
要使上述推导过程中所作的假设成立,需要符合5个条件:①通道所在波长区间的普朗克函数要满足积分中值定理的要求;②通道所在波段的普朗克函数具有较好的线性度,可以进行泰勒级数一阶展开;③所选通道对应的 ∂B(v,Ts)/∂v(v,)/∂v和 ∂I(v,T)/∂v的值近似相等; ④通道内的大气平均辐射亮度Ba(v)近似相等;⑤具备有效的方法求解γ值。
3MODTRAN4模拟和IASI实测数据对比
IASI(infrared atmospheric sounding interferometer,红外大气探测干涉仪)是搭载在欧洲极轨气象卫星METOP-A上的探测器,有8461个通道,以0.25 cm-1的光谱分辨率覆盖了3.7 ~15.5 μm 波长区间,是目前可以获得的比较好的红外光谱数据源[10]。以获取IASI数据时的大气参数作为MODTRAN模拟时的输入参数,将模拟结果与IASI实测数据相比较,如图1所示。
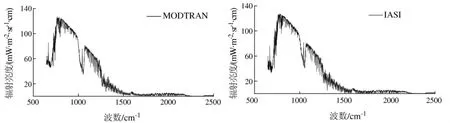
图1 MODTRAN 4模拟(左)和IASI实测(右)谱线对比Fig.1 Simulation of MODTRAN(left)vs.Measurements of IASI(right)
从图1可以看出,MODTRAN模拟和IASI实测的谱线在形态和值的大小上都非常接近,说明用MODTRAN进行相关模拟分析的结果是比较可信的。
4 劈窗算法的通道特性模拟分析
4.1 大气贡献辐射亮度的近似计算
大气辐射传输方程中的积分项表示大气贡献的辐射能量。计算通道区间在2 μm~1 cm、温度为233.5 K,273.5 K,310 K 和 373.5 K 时的 Planck 函数曲线如图2所示。
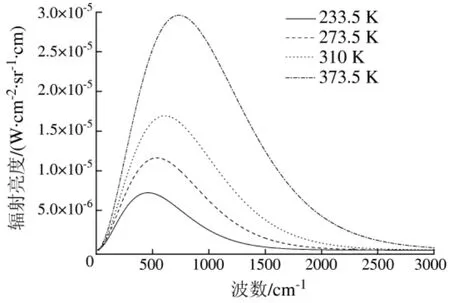
图2 不同温度下的Planck函数曲线Fig.2 Planck curves with different temperatures
从图2可以看出,Planck函数曲线满足中值定理的条件,可以用中值定理近似表达积分项所代表的大气贡献的辐射亮度。
4.2 通道区间Planck函数的线性分析
利用MODTRAN 4模拟了在中纬度夏季大气模式下,假定海洋表面发射率为1、海洋表面温度为300 K,大气柱状水汽含量为5.0 g/cm2条件下的大气顶层辐射亮度曲线,如图3所示。

图3 通道光谱辐射亮度的线性分析Fig.3 Linear analysis of channel spectral radiance
从图 3可以看出,在 10~13.3 μm(1000~750 cm-1)和 8 ~9.09 μm(1250 ~1100 cm-1)2 个通道区间内,波数和辐射亮度间具有较好的线性关系,这种线性关系不会随着温度、大气柱状水汽含量的改变而改变。
4.3 ∂B(v,T)/∂v随温度的变化
在劈窗算法的推导过程中,若 ∂B(v,Ts)/∂v,/∂v 和 ∂I(v,T)/∂v 存在近似相等关系,则有助于辐射传输方程的简化。观察这3项发现,其主要差异在于温度。为了分析∂B(v,T)/∂v随温度的变化趋势,分别计算其在温度275 K,280 K,285 K,290 K,295 K,300 K,305 K,310 K 和 315 K时的值。以275 K时的计算结果为基点,分别求与其他温度状态下的计算结果差值,即 ∂B280,…,315(v,T)/∂v- ∂B275(v,T)/∂v。以 ∂B(v,T)/∂v 的差值 δ作为纵坐标轴变量,以波数作为横坐标轴变量,不同温度下的∂B(v,T)/∂v变化趋势如图4所示。
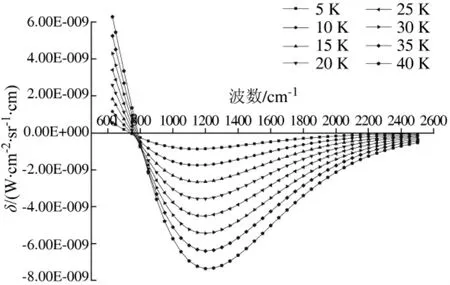
图4 ∂B(v,T)/∂v随温度的变化Fig.4 Changes of ∂B(v,T)/∂v with different temperatures
从图4可以看出,靠近800 cm-1处的∂B(v,T)/∂v随温度的变化比较小,位于10 ~13.3 μm(1000 ~750 cm-1)区间的通道因 ∂B(v,Ts)/∂v∂v和 ∂I(v,T)/∂v的近似相等导致的误差会小于位于8 ~9.09 μm(1250 ~1100 cm-1)区间的通道。
4.4 通道大气辐射亮度(v)
为了分析大气辐射的影响,我们在假定下垫面温度接近绝对零度、大气模式选择中纬度夏季条件下,利用MODTRAN4模拟大气的分光辐射亮度,如图5所示。
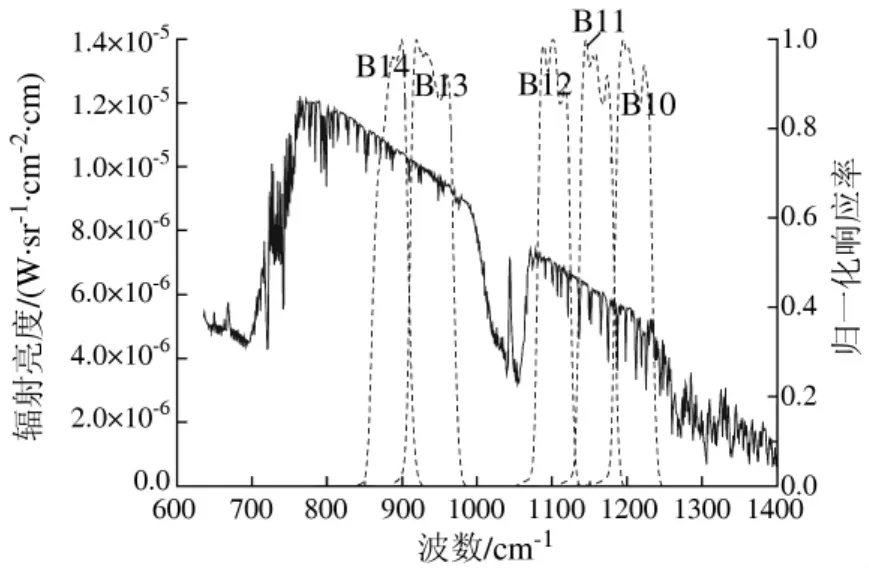
图5 通道大气辐射亮度Fig.5 Channel atmospheric radiance
从图5可以看出,在热红外大气窗区内的10~13.3 μm(1000 ~750 cm-1)和 8 ~9.09 μm(1225 ~1100 cm-1)波长内,大气辐射亮度随波数的变化起伏较小,即在2个通道设置比较靠近的条件下,图中虚线表示的是ASTER 5个热红外通道(B10—B14)的通道响应函数。相邻通道间的大气辐射亮度的差是比较小的,从而可以近似得到的关系。
4.5 γ值的求解
Mcmillin提出的利用迭代法求解γ的基本思想是:已知2个通道或者1个通道2个角度的实测辐射亮度I1和I2,同时给定一个目标处的辐射亮度Bsi,然后通过热红外辐射传输模式得到2个计算辐射亮度I1i和I2i(i表示迭代次数);将Bsi,I1i和 I2i代入式(11),计算 γi; 再将 γi,I1和 I2代入式(11),计算新的Bsi;重复上述过程,直至Bsi的值前(Bsi_a)后(Bsi_b)之差小于某一个阈值,迭代过程结束(图6)。
为了验证上述迭代法求解γ的效果,以MODTRAN作为大气辐射传输模拟工具,利用ASTER热红外探测器5个通道的响应函数来分析迭代求值模型。选 择 ASTER B11,B12,B13 和 B14,将B 13和B14作为A组,以909 cm-1(11 μm)作为

图6 γ的迭代计算Fig.6 γ iterative calculation
参考波数;将B11和B12作为B组,以1111 cm-1(9 μm)作为参考波数。选择模拟时的大气模式为中纬度夏季大气(MLS),下垫面温度为295 K,其他参数设为默认值。
对于 A组,温度为 295 K、波数为 909 cm-1(11 μm)时的Planck函数值为1.074772E-5 W·cm-2·sr-1·cm;B13的光谱辐射亮度I2=9.63986E-6 W·cm-2·sr-1·cm;B14的光谱辐射亮度I1=1.045429E-5 W·cm-2·sr-1·cm,如表1所示。

表1 ASTER B13和B14的γ迭代①Tab.1 γ iteration of ASTER B13 and B14
对于 B组,温度为295 K、波数为1111 cm-1(9 μm)时的Planck函数值为7.271688E-6W·cm-2·sr-1·cm;B11的光谱辐射亮度I2=5.734018E-6 W·cm-2·sr-1·cm;B12的光谱辐射亮度I1=6.688973E-6 W·cm-2·sr-1·cm,如表2所示。

表2 ASTER B11和B12的γ迭代①Tab.2 γ iteration of ASTER B11 and B12
通过对A组和B组的数值模拟分析,尽管2组的参考波数不同,但都在较少的迭代次数下收敛。其中,有2个比较关键的问题:①如何给出迭代初始值Bsi;②计算I1i和I2i所使用辐射传输模式。这二者关系到迭代时收敛的速度。在上述模拟时,将I1作为迭代初始值,同时使用MODTRAN 4作为计算I1i和I2i的辐射传输模式。
5 结论
针对劈窗算法基本公式推导过程中所提出的问题,结合星载探测器的通道响应函数和大气辐射传输模式的模拟数据进行了讨论,得出如下结论:
1)以Planck函数为核函数的大气辐射积分项满足积分中值定理的条件,可以进行Planck函数近似计算,且在 10 ~13.3 μm(1000 ~750 cm-1)和8 ~9.09 μm(1250 ~1100 cm-1)区间内,Planck 函数与波数之间存在较好的线性关系;
2)在所研究的波长范围内,相邻通道的大气辐射亮度非常接近,利用这一特点可以最大可能地削弱大气影响;
3) 虽然 ∂B(v,Ts)/∂v和 ∂I(v,T)/∂v在10 ~13.3 μm(1000 ~750 cm-1)区间内的近似相等关系优于8~9.09μm(1250~1100 cm-1)区间的,但是利用迭代法求解γ值和辐射亮度对此并不敏感,所要考虑的是迭代初始值和计算效率问题。因此,将8 ~9.09 μm(1250 ~1100 cm-1)波长区间通道获取的热红外遥感数据用于劈窗算法进行地表温度反演具有一定的可行性。
[1]Schott J R,Volchok W J.Thematic Mapper Thermal Infrared Calibration[J].Photogrametric Engineering and Remote Sensing,1985,51(9):1351 -1357.
[2]覃志豪,Zhang M H,Karnieli A,等.用陆地卫星TM6数据演算地表温度的单窗算法[J].地理学报,2001,56(4):456 -466.Qin Z H,Zhang M H,Karnieli A,et al.Mono- window Algorithm for Retrieving Land Surface Temperature from Landsat TM6 Data[J].Acta Geographica Sinica,2001,56(4):456 - 466(in Chinese with English Abstract).
[3]Price J C.Land Surface Temperature Meas urements from the Split Window Channels of the NOAA7 Advanced Very High Resolution Radiometer[J].Journal of Gephysical Research,1984,89(D5):7231-7237.
[4]Gillespie A,Rokugawa S,Matsunaga T,el al.Temperature and Emissivity Seperation Algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer(ASTER)Images[J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(4):1113-1126.
[5]Wan Z M,Li Z L.A Physics- based Algorithm for Retrieving Land Surface Emissivity and Temperature from EOS/MODIS Data[J].IEEE Transactions on Geoscience and Remote Sensing,1997,35(4):980-996.
[6]Planck M.On the Law of Distribution of Energy in the Normal Spectrum[J].Annalender Physik,1901,4:553.
[7]Michels T E.Planck Functions and Integrals:Methods of Computation[R].Washingtion D C:National Aeronautics and Space Administration,1968.
[8]Chandrasekhar S.Radiative Transfer[M].New York:Dover Publication,1960.
[9]Mcmillin L.Estimation of Sea Surface Temperatures from Two Infrared Window M - easures with Different Absorption[J].Joural of Geophysical Research,1975,80(C36):5113 -5117.
[10]CNES and EUMETSAT.IASI Program[EB/OL].http://smsc.cnes.fr/IASI/.
Discussions on Using Channels of Split-window Algorithm to Retrieve Earth Surface Temperature
MENG Peng1,2,HU Yong1,GONG Cai- lan1,LI Lin1,2
(1.Shanghai Institute of Technical Physics,CAS,Shanghai 200083,China;2.Graduate School of Chinese Academy of Sciences,Beijing 100049,China)
Being simple and effective,the split-window algorithm based on thermal infrared remote sensing is widely used to retrieve surface temperature.The method mainly uses thermal infrared bands in 10 ~ 13.3 μm(1000 ~750 cm-1)range,neglecting bands in 8 ~9.09 μm(1250 ~1100 cm-1)range.This paper analyzes the process of deriving the formula of the split-window algorithm,summarizes the problems associated with the channel setting and makes numerical simulation analysis in the 10 ~13.3 μm(1000 ~750 cm-1)and 8 ~9.09 μm(1250 ~1100 cm-1)ranges to solve the problems.The results show that split-window algorithm derived on the basis of this approach has similar performance in both 10 ~13.3 μm(1000 ~750 cm-1)and 8 ~9.09 μm(1250 ~1100 cm-1)spectral ranges.Therefore,it can be concluded that the spectral range in 8 ~ 9.09 μm(1250 ~ 1100 cm-1)range can also be used to derive split- window algorithm for thermal remote sensing.
split-window algorithm;Earth surface temperature;thermal infrared band;MODTRAN
TP 79
A
1001-070X(2012)04-0016-05
2011-12-19;
2012-03-08
中国科学院上海技术物理研究所创新专项(编号:Q-ZY-19)及国家科技支撑计划课题(编号:2012BAH31B02)共同资助。
10.6046/gtzyyg.2012.04.03
孟 鹏(1983-),硕士研究生,主要从事红外遥感数据应用研究。E-mail:bushhouse@126.com。
(责任编辑:刁淑娟)

