基于四级网格划分的待匹配路段初筛方法研究

吴 伟，吴堑虹，邓吉秋

(中南大学地球科学与信息物理学院，长沙 410083)

基于四级网格划分的待匹配路段初筛方法研究

吴 伟，吴堑虹，邓吉秋

(中南大学地球科学与信息物理学院，长沙 410083)

在地图匹配过程中，待匹配路段初筛过程是影响其时间效率的关键。鉴于现有的路段初筛方法在最大检索范围的控制上仍有进一步缩减的空间，提出了一种四级交错式网格筛选方法。通过对深圳市GPS定位数据的检索实验表明:该方法可有效缩减候选路段的筛选范围，并在保证筛选范围的稳定性上优于现有的方法;通过有效控制候选路段的检索范围，进一步减少了检索时间。该方法在车载导航和大规模GPS数据处理等领域具有很大的应用价值。

GPS;地图匹配;待匹配路段初筛;网格划分

0 引言

在GPS数据应用领域，地图匹配作为核心处理环节［1］已有了广泛研究，其目的在于从路网中选择出GPS点所处的最有可能路段，然后计算出GPS点在该道路上的精确位置［2］。地图匹配算法一般包括GPS数据校验、匹配道路初筛、特定算法求解以及定位点求取［3］4个主要环节。其中，匹配道路初筛是指以GPS点为中心，在给定误差范围内获取落在该范围内的道路集合。现有的初筛方法主要有直接计算法、移动窗口法［4］、交错式移动窗口法［5］和多级网络划分的匹配道路初筛法［3］等等。直接计算法是指将整个路网作为候选道路，该方法效率较低，极少被使用;移动窗口法采用平面式网格划分结构，将包括待定位点所在网格在内的9个相邻单元格作为检索范围，其最大检索范围为9个单元格;交错式移动窗口法在平面式网格之上新增一级网格，并使检索范围限定在1个或4个单元格之内，该方法将最大检索范围缩小到4个单元格;多级网络划分的匹配道路筛选方法采用与平面式网格类似的划分结构，能将检索范围限定在1，2或4个单元格内。以上方法都在不同程度上缩减了检索范围，但不能保证检索范围的稳定性。为此，本文提出了四级网格划分的待匹配路段初筛选方法。该方法将检索范围始终限定在一个单元格内，保证了检索范围的稳定性。

1 方法设计

1.1 网格划分与数据组织

首先，根据图幅范围和定位精度误差半径R将整个图幅分为M×N个、边长L=K×R的单元格(K，M，N为≥2的整数)。为精确描述待定位点在一级单元格内的相对位置，对每个单元格进行4×4细分，形成16个逻辑子网格;依次编号后，其中［6，7，10，11］号子网格构成单元格的核心区。然后，以任意相邻4个单元格的交点为中心，建立(M－1)×(N－1)个单元格，完成第二次划分;第三次划分是在一级网格中以左右相邻单元格的公共边的中点为中心建立N×(M－1)个单元格。最后，以一级网格上下相邻单元格公共边的中点为中心，建立(N－1)×M个单元格，构成第四级网格。

各级网格中的单元格大小相同，且都采用统一的编号规则:即以左下角开始，从左向右，从下往上依次编号。图1中给出了四级网格划分及编号示意图。

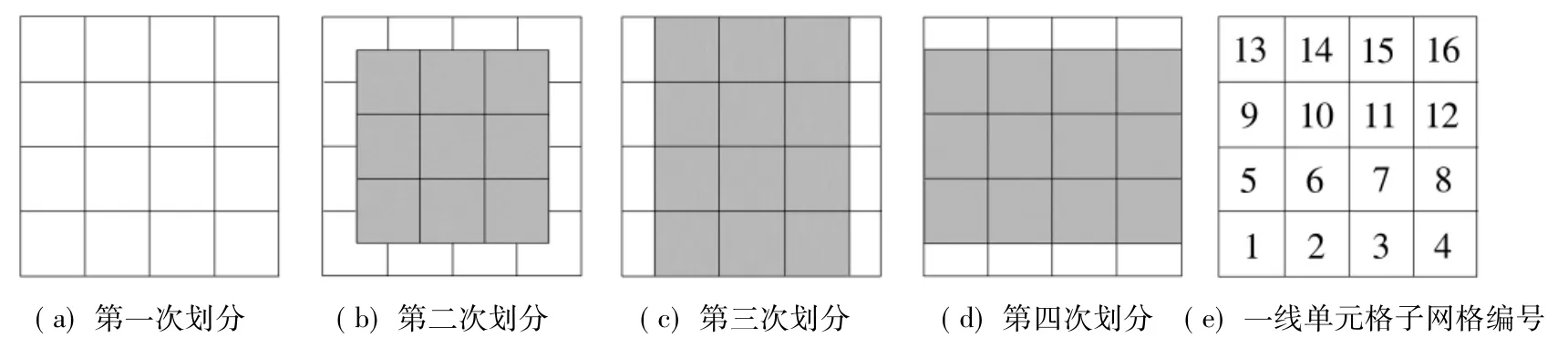
图1 四级网格划分方法Fig.1 Four－level grid division method

网格划分完毕后，要建立道路和各级单元格之间的索引关系，可用图2所示的关系模型，将索引数据保存在数据库中。

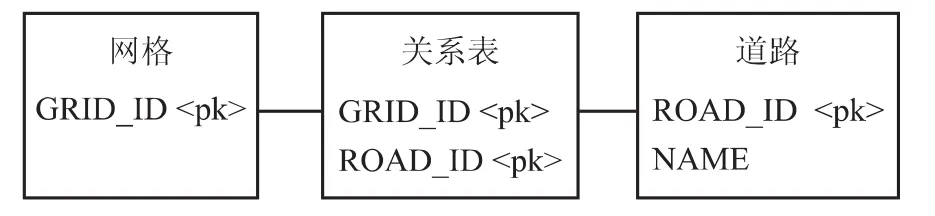
图2 网格与道路索引关系模型Fig.2 Index model between grids and roads

1.2 网格筛选算法

按上述方法建好网格与道路索引关系后，使用本文提出的待选道路范围筛选算法建立待定位点坐标与其所在网络级别及编号的映射关系。

1.2.1 理论依据

Taylor［6］认为，单频 GPS 接收机定位通常以距原始定位点100 m内的道路为计算路段，车辆位于这些路段的置信度为95%。所谓置信度［7］，是指特定个体对待特定命题真实性相信的程度。本文基于该原理，提出道路初筛中待定位点所在网格的置信度计算方法。即:以待定位点为中心，用定位精度R为半径画圆，以该圆与待定位点所在网格做交集，以所得交集的面积和该圆的面积比作为该网格置信度。其公式为

式中:p为网格置信度;S为以待定位点为中心、以定位精度R为半径所得的圆;T为待定位点所在网格;area为面积计算函数。由式(1)可知，p的取值范围为［0～1］。

图3(网格T的边长L=4R)给出了3种不同情况下网格置信度的示意图。

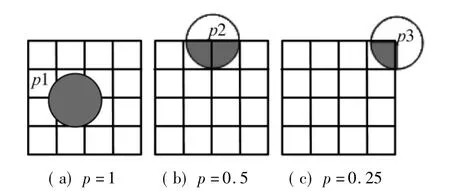
图3 网格置信度示意图Fig.3 Examples of grid confidence level

如图3所示，当点落在网格的核心区内，网格的置信度为最高值1(图3(a));当点落在网格的边界上时，网格置信度降至0.5(图3(b));当点落在网格的角点上时，网格置信度降至0.25(图3(c))。当p＜0.25时，待定位点已经不在网格范围内。可见，待定位点离网格核心区越近，p的取值越接近于1，该网格作为候选道路的检索范围的可信度就越高。基于这种思想，本文设计了基于四级网格划分的候选道路范围筛选算法。

1.2.2 计算方法

设图幅左下角坐标为(Left，Bottom)，右上角坐标为(Right，Top)，一级网格数量为M×N，单元格大小为(△x，△y)，待定位点 q的坐标为(x，y)。则由

可计算出点q在一级网格中的行号n、列号m;由

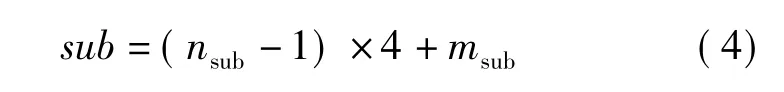
可计算出点q所在的子网格编号。式中nsub，msub分别为点q在一级网格单元格内的子行号和子列号，可分别由

计算出。式中［］为向上取整符号。已知m，n，sub，便可用

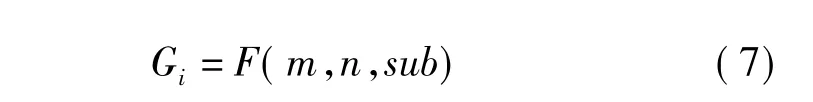
求得点q的候选道路范围。式中:Gi为第i级网络单元格编号，i=1，2，3，4;F为筛选函数。根据 m，n，sub的不同取值范围，F采用2类略有差异的求解算法:当2≤n≤N－1且2≤m≤M－1时的“非边界区域求解算法”和当m，n不在以上取值范围内时的“边界情况下的求解算法”。

1.2.2.1 非边界区域求解算法

非边界情况下的求解算法可简述为:如果点q所在子网格sub为Gi的核心区，则将点q的候选道路检索范围限定在 Gi内。当2≤n≤N－1且2≤m≤M－1时，筛选函数F的求解伪算法程序为

IF sub=［6，7，10，11］THEN G1=(n －1)M+m;

IF(2≤n≤N －1)＆＆(2≤m≤M －1)THEN{

IF sub=1 THEN G2=(n－2)(M－1)+(m－1);

ELSE IF sub=4 THEN G2=(n－2)(M－1)+m;

ELSE IF sub=13 THEN G2=(n－1)(M－1)+(m－1);

ELSE IF sub=16 THEN G2=(n－1)(M－1)+m;

ELSE IF sub=［5，9］THEN G3=(n －1)(M－1)+(m－1);

ELSE IF sub=［8，12］THEN G3=(n －1)(M－1)+m;

ELSE IF sub=［2，3］THEN G4=(n －2)M+m;

ELSE IF sub=［14，15］THEN G4=(n －1)M+m;}

笔者以图4中的3×3四级网格为例，说明求解过程。

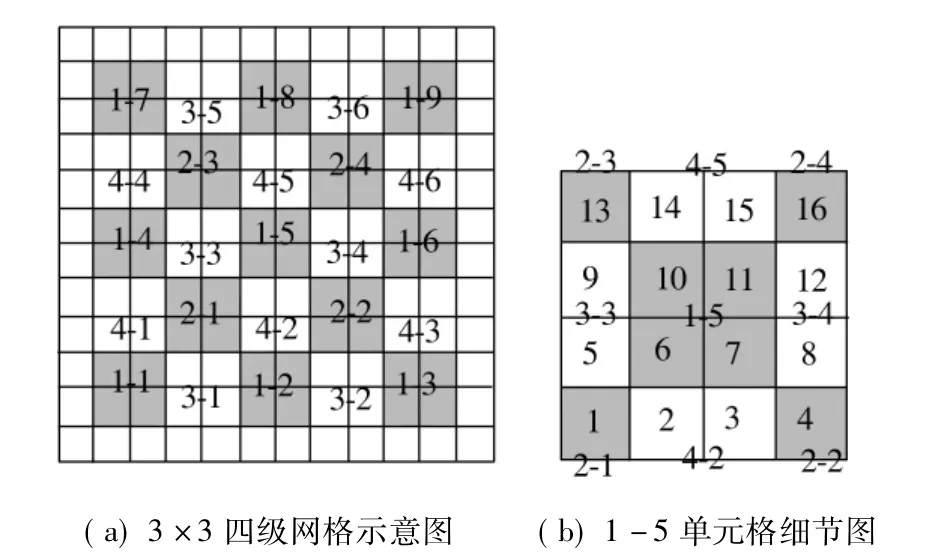
图4 四级网格样例图Fig.4 Example of four－level grid

图4(a)以“网格级别－单元格编号”的方式(如1－5)标出各级网格单元格的编号，其中编号为1－5单元格放大后如图4(b)所示。设点q所在子网格编号为sub，则有

①sub=6，7，10，11，q∈1 －5;

②sub=1，q∈2－1; ③sub=4，q∈2－2;

④sub=13，q∈2－3; ⑤sub=16，q∈2－4;

⑥sub=5，9，q∈3 －3; ⑦sub=8，12，q∈3 －4;

⑧sub=2，3，q∈4 －2; ⑨sub=14，15，q∈4 －5。

由图4(b)可知，非边界单元格的16个子网格均为各级网格单元格的核心区，因此在非边界情况下，本方法可保证检索范围的置信度最高且将检索范围限定在1个单元格内。

1.2.2.2 边界情况下的求解算法

当n=1或N，m=1或M时，点q落在一级网格的边界上，此时的求解算法可简述为:优先按核心区判定检索范围，如果子网格sub不属于任何一级网格单元格的核心区，则选择置信度最大的单元格作为检索范围。

本文以图4(a)中的1－1单元格为例，说明在这种特殊情况下的求解原理。将单元格1－1和1－2放大后如图5所示。

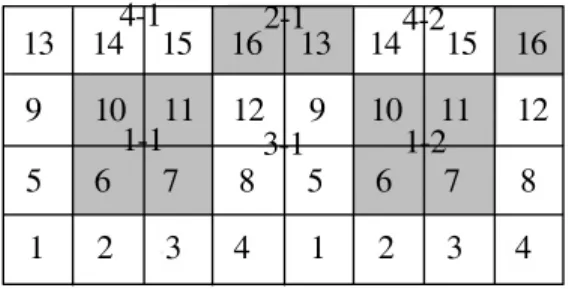
图5 边界网格示意图Fig.5 Example of boundary grids

当点q落在1－1单元格内时，设其所在子网格编号为 sub，则有

①sub=1，2，3，5，9，6，7，10，11，q∈1 －1;

②sub=16，q∈2 －1;

③sub=4，8，12，q∈3 －1;

④sub=13，14，15，q∈4 －1。

第 6，7，10，11，8，12，14，15，16 号子网格分别是各级网格单元格的核心区，可用本节算法求得对应的网格编号。而对于 1，2，3，4，5，9，13 号子网格而言，它们不属于任何一级网格单元格的核心区，因此要根据网格置信度最大化原则判定检索范围。其中1，2，3，5，9号子网格只在1－1的单元格的范围内，如果点q落在它们当中，只有1－1号单元格作为候选检索范围。而4，13号子网格例外，它们位于2个单元格的共享范围内。以4号单元格为例，其同时在1－1和3－1的范围内，当点q落在其内时，就有2个单元格作为候选检索范围，但因3－1的置信度大于1－1的置信度，故将检索范围限定在3－1内。同理，当点q落在13号子网格内时，有1－1和4－1作为候选检索范围，但4－1的置信度大于1－1，因此检索范围限定在4－1内。根据这种判定原则，结合4个顶角和4条边的各异情况，可编制出相应的筛选算法解决非核心区情况下的范围判定。

2 实验与分析

笔者在路网数据量为60932条的深圳市地图内，按400 m×400 m建立四级网格，用Postgresql数据库保存网格、道路及两者间的索引关系。用5辆出租车(尾号分别为 G10，G23，G27，G31，G38)，在2009年08月01日00:00～24:00时段内的20000条GPS定位数据，在2 G内存，主频为2 GHz双核处理器硬件平台上，分别用移动式窗口法、交错式移动窗口法、多级网络划分法和四级网络划分法，按5000，10000，20000条的 GPS数据量分3组进行检索实验。其中，每种方法在每一组内做6次检索，取6次检索时间的平均值为该方法在该组内的检索时间，经实验后得到各种方法的检索时间效率对比，其结果如图6所示。

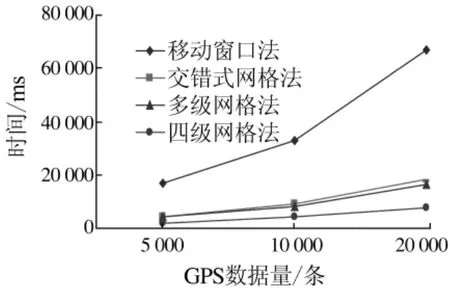
图6 各方法效率对比Fig.6 Efficiency comparison between proposed method and tradition ways

从图6可以看出，在同等GPS数据量条件下，四级网格筛选技术所花的检索时间均比其他3种方法所花时间少，且平均检索时间约为现有最优方法所花时间的1/2。在不同GPS数据规模下，因数据量的增加导致各种方法的检索时间都有所上升，但四级网格筛选技术的检索时间依然最少，与现有最优方法的检索时间比仍保持为1/2。在以单元格为单位，决定待匹配路段检索范围时的不同选择策略是导致4种方法在检索时间上存在差异的根本原因。由于这种差异，使得在相同路网集上进行单个GPS点的待匹配道路初筛时，四级网格技术取得的路段数据量最小，进而为接下来的匹配过程从减少路段数据量角度辅助提升单个点的匹配校正时间效率。综合对比不同初筛方法，以四级网格划分的待匹配路段初筛方法在缩减最大检索范围和控制检索范围的稳定性上占有绝对优势。

3 结论

本文的理论分析与实验结果表明，基于四级网络划分策略的待匹配路段筛选方法在减少筛选范围的能力和控制检索范围的稳定性上具有显著的优越性。因该方法的实现不涉及到复杂的数学计算，并且可大大地缩短初选道路的检索时间，因此可广泛应用于各类匹配应用中。

［1］薛 明，吕卫锋，诸彤宇.浮动车信息处理系统关键技术的研究［J］.微计算机信息，2006，22(11 －1):244 －246.Xue M，Lv W F，Zhu T Y.Study on the Key Technology of Floating Car Information Processing System［J］.Microcomputer Information，2006，22(11 －1):244 －246(in Chinese with English Abstract).

［2］唐进君，曹 凯.基于多准则融合的信任理论地图匹配算法［J］.测绘科学，2009，34(5):14 －15.Tang J J，Cao K.A Map －matching algorithm Based on Multi－criteria Fusion Using Belief Theory［J］.Science of Surveying and Mapping，2009，34(5):14 －15(in Chinese with English Abstract).

［3］冯金巧，孙占全，刘 威.基于多级网络划分的匹配道路初筛方法研究［J］.交通信息与安全，2010，28(4):5 －8.Feng J Q，Sun Z Q，Liu W.Primary Screening Method of Matching Road Based on Multilevel Division of Road Network［J］.Journal of Transport Information and Safety，2010，28(4):5 － 8(in Chinese with English Abstract).

［4］苏慧敏，周 鹏，陈 哲.基于DS证据理论的GPS/MM组合系统车辆定位算法［J］.北京航空航天大学学报，2001，27(2):157 －160.Su H M，Zhou P，Chen Z.Study of GPS/MM Integrated Navigation System for Vehicle Positioning Based on DS Evidence Reasoning［J］.Journal of Beijing University of Aeronautics and Astronautics，2001，27(2):157 －160(in Chinese with English Abstract).

［5］杨新勇，黄圣国.地图匹配算法中的待配路段快速筛选方法［J］.华南理工大学学报:自然科学版，2004，32(2):62 －66.Yang X Y，Huang S G.Quick Road Choice Method in Map Matching Algorithms［J］.Journal of South China University of Technology:Natural Science Edition，2004，32(2):62 － 66(in Chinese with English Abstract).

［6］Taylor G，Blewitt G.Road Reduction Filtering Using GPS［C］//3th AGILE Conference on Geographic Information Science－helsinki.Finland:(s.n.)，2000:114 －119.

［7］赵国求.经典概率与量子概率［J］.武汉工程职业技术学院，2002，14(1):31 －32.Zhao G Q.Traditional Probability and Quantum Probability［J］.Journal of Wuhan Engineering Institute，2002，14(1):31 － 32(in Chinese with English Abstract).

Research on Primary Filtering Method for Pre－matching Road Sections Based on Four－level Grid Division

WU Wei，WU Qian －hong，DENG Ji－qiu
(School of Geosciences and Info－physics，Central South University，Changsha 410083，China)

The primary filtering of the pre－matching road sections in the map matching algorithm，in which GPS point finds the closest approximation road for driving，is the key factor of the time efficiency.There is a great deficiency of redundant searching range in the existing primary filtering methods.To reduce the searching range，this paper proposes a novel four－level interlaced grid filtering method，which can efficiently narrow the searching range.It is indicated that the method proposed in this paper is superior to the existing methods on the premise of guaranteeing the stability of the filtering range，as shown by experimental comparisons with many traditional methods based on GPS data.This method has high application values in many fields such as the vehicle navigations and large－scale GPS data processing because it can further reduce the searching time by controlling the searching range effectively.

GPS;map matching;primary filtering of pre－matching road sections;grid division

TP 79

A

1001－070X(2012)04－0026－04

2012－01－08;

2012－08－29

国家水体污染控制与治理科技重大专项课题(编号:2009ZX07212－001－06)。

10.6046/gtzyyg.2012.04.05

吴 伟(1987－)，男，硕士研究生，主要研究领域为并行计算和网络地理信息系统。E－mail:xmzfighting@126.com。

(责任编辑:刁淑娟)