卡诺图化简数学新方法

叶 腾，朱桂英

（1.上海交通大学安泰经济与管理学院，上海 200240；2.河北工程大学装备制造学院，河北邯郸 056029）

卡诺图化简数学新方法

叶 腾1，朱桂英2

（1.上海交通大学安泰经济与管理学院，上海 200240；2.河北工程大学装备制造学院，河北邯郸 056029）

提出了卡诺图化简中获得卡诺圈合并结果的数学方法。根据卡诺图制图原理，这种数学计算方法的要点在于：用2个最小项对应的十进制数之差找到消去变量；从卡诺圈的某个最小项中去掉相应消去变量得到合并结果。该方法在卡诺图（尤其变量数较多的）化简中，能更准确、更迅速地获得卡诺圈合并结果，并可应用于计算机辅助卡诺图化简逻辑函数。

卡诺图；应用数学方法；简化法

逻辑函数化简是数字逻辑和数字电路分析中的重要内容，目前主要有代数化简法、表格化简法和卡诺图化简法。代数方法是基于布尔代数基本运算公式进行化简的方法，这种方法要求操作者掌握一定的技巧，并对最简结果有一定的判断能力。卡诺图化简法是6个以下变量逻辑函数化简最简便而常用的方法。

近年来，人们对卡诺图进行了多方面的研究和拓展，包括卡诺图镜像画圈法［1］、最小项使用的重复次数识别技巧［2］、填图技巧［3］、卡诺图降维简化法［4］、卡诺图的计算机辅助实现［5］等方法，对如何快速、准确地确定卡诺圈合并项结果却没有很好的解决方法，导致在实际应用（尤其是在四变量、五变量、六变量卡诺图中）时，人们容易混淆变量位置，以致误读最小项合并结果。笔者提出的卡诺图化简数学方法可解决上述问题。

1 基本步骤

1.1 画卡诺图

在“与 －或”表达式的基础上，画出逻辑函数的卡诺图，步骤如下［6］：

1）画出函数变量的卡诺图。

2）在图中标示每一个乘积项所包含的最小项，就得到逻辑函数的卡诺图。

其中，如果乘积项为最小项，则可直接转换成数字代码对应填入卡诺图。在二进制对应数中，原变量代表该位为1，反变量代表该位是0。这样将乘积项（即最小项）转化为二进制对应数，再将二进制数转化为十进制数，填入对应编号的小方格中。如，AB′C＝101＝5，所以填入m5。如表达式不是最小项表达式，但是“与－或”表达式可将其先转化成最小项表达式，再填入卡诺图，再按上述规则填入。也可根据乘积项是最小项的公因子这一特点直接观察填入。

1.2 画卡诺圈

画圈规则与传统卡诺圈规则相似，具体规则如下［7］：

在标示出的相邻最小项中画圈，尽量画大圈，但每个圈内只能含有2n（n＝0，1，2，…）个相邻项。要特别注意对边相邻性和四角相邻性。

圈的个数尽量少。在新画的包围圈中至少要含有1个未被圈过的标识方格，否则该包围圈是多余的。卡诺图中所有标示过的方格均要被圈过，即不能漏下标示过的最小项。

1.3 合并卡诺圈中的最小项

任意选取卡诺圈中的最小项，写出由变量组成的逻辑式（由于系数小的最小项逻辑式相对容易写，所以一般选取卡诺圈中系数最小的最小项）。然后找出卡诺圈中系数之差为2n的所有差值，从逻辑式中消去所有差值对应位的变量。如miniterm1＝x1，miniterm2＝x2，w＝log2｜x1－x2｜＋1，则消去从右至左第w位的变量。将所有差值对应变量消去后的逻辑式即为卡诺圈合并结果。

1）对包含2n个最小项的卡诺圈来说，只需要找到n种不同的2n的差，如1，2，4，8等，然后将这些差所代表的变量从卡诺圈中系数较小的最小项中去掉，即为该圈的最终合并结果。

2）找差技巧：①将左上角的数，先分别和它右相邻数、下相邻数作差，再分别和圈中首行行尾、首列列尾数作差，这5个位置一般就可以把差找全；②将圈中最大数减去最小数，并将差表示成若干个2n的和，每一个2n必定是一种两项差。

1.4 写出最简“与 －或”表达式

将所有卡诺圈的计算结果相与（用加号相连），即为最终合并结果。

2 实例展示

图1 四变量卡诺图Fig.1 Four－variable map

例1［8］化简F（A，B，C，D）＝∑（0，1，2，6，8，9，10）。

解 传统方法如下：

第1步，画出四变量卡诺图，见图1。

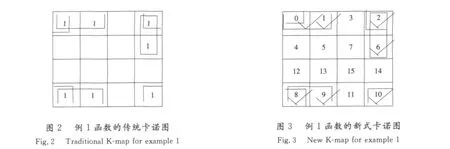
第2步，画出传统卡诺图，见图2，观察对应变量，计算逻辑函数结果。

新算法见图3，其中A为8，B为4，C为2，D为1，图中有以下3个卡诺圈。

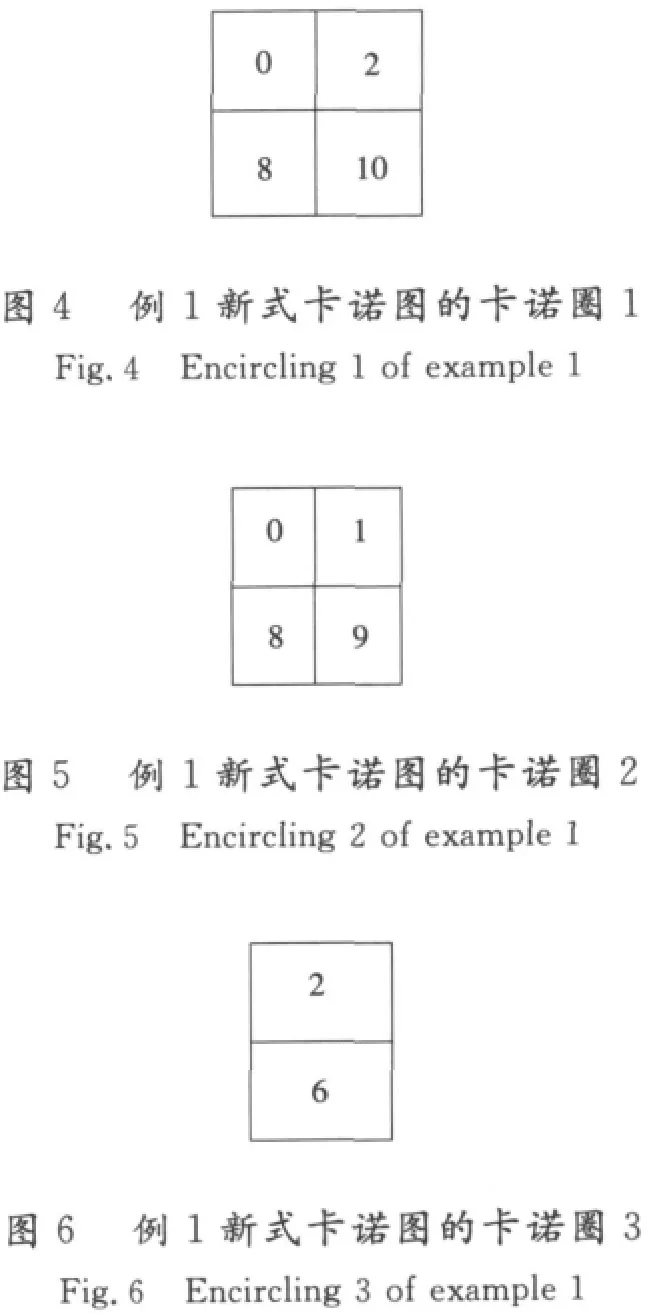
卡诺圈1（见图4）：min｛0，2，8，10｝＝0＝A′B′C′D′，该卡诺圈包含4个最小项，4＝22，因此需要找2个不同的2的幂的差。8－0＝8，所以消掉的变量是A；2－0＝2，所以消掉的变量是C。消掉A，C，为B′D′。

卡诺圈2（见图5）：min｛0，1，8，9｝＝0＝A′B′C′D′，该卡诺圈包含4个最小项，4＝22，因此需要找2个不同的2的幂的差。1－0＝1，所以消掉的变量是D；8－0＝8，所以消掉的变量是A；A′B′C′D′中消掉A，D，为B′C′。

卡诺圈3（见图6）：6－2＝4所以消掉的变量是B，min｛2，6｝＝2＝A′B′CD′，消掉B为A′CD′。所以原函数结果是F（A，B，C）＝∑（0，1，2，6，8，9，10）＝B′C′＋B′D′＋A′CD′。

例2 化简F（A，B，C，D，E）＝∑（4，5，6，7，9，11，13，15，16，24，27，31）。

解 传统方法如下.

第1步，画出五变量卡诺图，见图7。

第2步，画出对应函数的传统卡诺图见图8。可见五变量用传统的卡诺图已经很难快速分辨合并后的结果。

卡诺图化简新方法计算如下（见图9）。

变量对应十进制数为A：16，B：8，C：4，D：2，E：1；图中共4个卡诺圈。

卡诺圈1（见图10）：min｛4，5，6，7｝＝4＝A′B′CD′E′。该卡诺圈包含4个最小项，4＝22，因此需要找2个不同的2的幂的差。5－4＝1，消掉的变量是E；6－4＝2，消掉的变量是D；A′B′CD′E′消掉D，E，即A′B′C。

卡诺圈2（见图11）：min｛9，11，13，15｝＝9＝A′BC′D′E。该卡诺圈包含4个最小项，同理需要找2个不同的2的幂的差。13－9＝4，消掉的变量是C；15－13＝2，消掉的变量是D；消掉变量C，D，即A′BE。

卡诺圈3（见图12）：min｛15，31，11，27｝＝11＝A′BC′DE。该卡诺圈包含4个最小项，同理需要找2个不同的2的幂的差。15－11＝4，消掉的变量是C；31－15＝16，消掉的变量是A；消掉A，C，即BDE。

卡诺圈4（见图13）：24－16＝8，所以消掉的是C。min｛16，24｝＝16＝AB′C′D′E′，消掉C，即AB′D′E′。

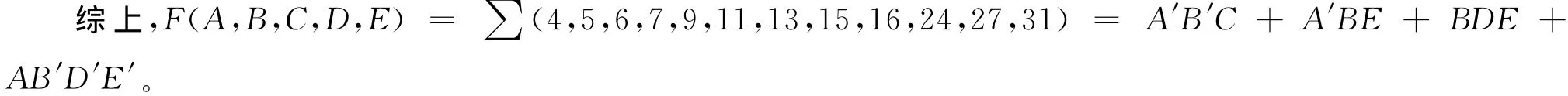
图7 五变量卡诺图Fig.7 Five－variable map

3 结 论

本文提出的卡诺图化简新方法是通过找到卡诺圈中系数较小的最小项并结合作差消元法确定卡诺圈中各项的合并结果，进而最终确定逻辑函数合并结果的逻辑函数简化法。该方法具有以下优点：

1）不需通过肉眼查找变量就能确定卡诺圈合并结果的简单易行的数学方法。即通过卡诺圈中最小项对应十进制数作差确定消去变量，再结合卡诺圈中系数最小的最小项最终合并结果。

2）普通卡诺图总共需画2张图，1张对应变量数的基本卡诺图，1张只包含0或1的函数卡诺图，填图需要先将最小项所对应的十进制表格标出，再另画1张图并在相应位置标0或1。而笔者提出的新方法只需画1张图，省略了另画图标0或1的步骤，可直接在十进制表格上操作。节省了1个步骤，可以使效率进一步提高。

3）由于这种方法基于作差与大小比较这2种数学运算，故可以在卡诺图的计算机辅助化简中大大简化逻辑运算。

［1］ 宋海声.化简逻辑函数的新方法［J］.西北师范大学学报（自然科学版）（Journal of Northwest Normal University（Natural Science）），2002，38（3）：37－41.

［2］ 韩建华.卡诺图化简多函数的简便方法［J］.华东地质学院学报（Journal of East China Geological Institute），1998，21（4）：392－395.

［3］ 江素云.使用卡诺图的技巧［J］.科协论坛（Science ＆Technology Association Forum），2009（12）：104－105.

［4］ 郭焕银.谈降维卡诺图化简逻辑函数的方法［J］.淮南师范学院学报（Journal of Huainan Teachers College），2001，3（2）：5－6.

［5］ 喻国平.逻辑函数的计算机辅助卡诺图化简［J］.南昌大学学报（工科版）（Journal of Nanchang University（Natural Science）），1996，18（3）：51－53.

［6］ 朱定华.数字电路与逻辑设计［M］.北京：清华大学出版社，2011.

［7］ 吴继娟.数字逻辑［M］.北京：人民邮电出版社，2008.

［8］ MORRIS M M.Computer System Architecture［M］.3rd ed.London：Prentice－Hall International，2002.

New mathomatical simplification method of Karnaugh map

YE Teng1，ZHU Gui－ying2
（1.Antai College of Economics and Management，Shanghai Jiaotong University，Shanghai 200240，China；2.Equipment Manufacturing College，Hebei University of Engineering，Handan Hebei 056029，China）

A mathematical method is provided to get the combination solution of variables in the encircling of Karnaugh map.Based on the basic theory of K－map，two key points of the method are：Ascertaining the complementary variables by the differences of the corresponding decimal indexes of the two miniterms；Eliminating the complementary variables from the corresponding miniterm in the encircling and qetting get the combination results.The method provides more efficient and accurate way to simplify logic functions based on K－map.It can also be applied to Karnaugh map of any number of variables and to simplification by K－map with computer assistance.

Karnaugh map；mathematical method；simplification method

O142

A

1008－1542（2012）03－0202－05

2012－02－17；责任编辑：张 军

叶 腾（1990－），女，河北大城人，主要从事信息系统及管理方面的研究。

朱桂英副教授。E－mail：Zhu0gui0ying＠163.com