基于压缩传感的混沌自适应控制

赵英宝，黄丽敏

（1.河北科技大学电气工程学院，河北石家庄 050018；2.河北科技大学现代教育技术中心，河北石家庄 050018）

基于压缩传感的混沌自适应控制

赵英宝1，黄丽敏2

（1.河北科技大学电气工程学院，河北石家庄 050018；2.河北科技大学现代教育技术中心，河北石家庄 050018）

提出了一种自适应混沌控制方法，仅根据输出时间序列，利用压缩传感辨识混沌系统的方程与参数，利用负反馈控制混沌系统到设定目标上。以Lorenz和Rössler系统为例说明时变结构系统的方程及参数的辨识与控制，首先估计出Lorenz系统方程并将其控制到固定点或周期振荡上，当系统结构从Lorenz变化到Rössler时可以快速辨识新结构及其参数，系统重新回到控制目标上。结果表明，与最小二乘法相比，该方法仅通过较少的数据即可实现模型结构与参数的同时估计，并有很高的估计精度，利用估计得到的模型和参数，再利用负反馈可以将混沌系统快速控制到设定目标上。

压缩传感；负反馈控制；模型估计；混沌控制；参数估计

动力学研究的正问题，即已知系统动力学方程和参数的情况下研究动力系统的演化或控制，已提出很多研究成果。而在未知方程或参数情况下，由系统输出时间序列辨识动力学方程和参数，属于动力学研究的逆问题，辨识系统方程和参数是对系统进行控制的重要前提。对于动力学系统的混沌控制，EDWARD等提出了混沌控制的OGY方法，它是一种不需要知道动力系统方程的控制方法［1］，之后提出了众多有效的混沌控制方法，从系统方程和参数均已知［2－3］到系统方程已知参数未知［4－5］，均得到了良好的效果。对于未知方程的动力学系统，DITTO等首次将OGY方法应用于未知系统方程的实际物理系统实验控制［6］；ALSING等利用人工神经网络［7］、KOBRAVI等利用模糊逻辑方法逼近动力学方程，再执行混沌控制，是一种离线控制方法，其辨识的结果并非动力学方程本身［8］；未知系统方程时，从完全未知的系统中估计方程存在困难，获知系统方程的先验知识，即指定系统的统一结构形式，GOUESBET等提出自治多项式结构［9］，BEZRUCHKO等提出非自治微分方程结构，然后利用最小二乘法估计方程和参数［10］，然而这种估计方法收敛速度慢且存在较大稳态误差。系统结构或参数的改变可能会产生边界危机等不期望现象，为了解决由输出时间序列估计系统动力学方程问题，WANG等提出了一种基于压缩传感的动力系统模型方程估计方法［11］。笔者基于该方法实现了未知系统方程的辨识及其混沌自适应控制。

利用压缩传感估计系统动力学方程，是基于可以将动力学方程表示成多变量幂级数展开形式，且仅有少数项的系数为非零这个基本假设，则模型系数可看成稀疏向量，动力学方程的估计转化为求解欠定线性系统。DONOHO和CANDÈS提出的压缩传感方法为求解此类欠定线性方程奠定了基础［12－13］，并证明了可以利用部分傅里叶系数重建原始信号［14］。由于幂级数系数与结构项的对应关系，利用压缩传感求解欠定线性系统可以实现动力学方程和参数的同时估计。压缩传感的优点在于信号的投影测量数据量远小于传统的采样方法，突破了香农采样定理的瓶颈［15］。利用压缩传感从含有少量观测数据中重建源信号，近来在图像处理［16］、数据通信［17］等领域得到了良好应用。

自适应控制都是已知系统方程而自适应估计系统参数。自适应控制和系统辨识密不可分。笔者提出的基于压缩传感的混沌自适应控制方法，首先利用压缩传感从观测时间序列中辨识出未知系统的动力学方程及其参数，再利用负反馈控制方法将其控制到目标点或周期振荡上。以Lorenz和Rössler系统为例说明时变结构系统的辨识和控制，该方法实现了Lorenz系统方程和参数的快速辨识并进行混沌控制，当系统在某时刻由Lorenz系统跳变到Rössler系统时，可以快速辨识出系统新的动力学方程和参数，实现控制混沌系统重新回到设定目标上。本控制策略对于实现时变结构非线性系统的混沌自适应控制非常有意义。

1 压缩传感原理

压缩传感是一种求解欠定线性系统稀疏解的方法，由于欠定线性系统中未知数的个数大于方程的个数，所以通常会有无穷多个解，但是如果系统有唯一的稀疏解，则人们可以通过压缩传感方法，利用较少的观测量便能重建稀疏解。

压缩传感过程可分为信号的稀疏化、构建稳态测量矩阵和利用重建算法恢复源信号3部分。压缩传感描述如下：已知某传感矩阵φ∈RM×N，且N≫M，稀疏向量x∈RN×1在矩阵φ下的输出为y∈RM×1，即y＝φx，压缩传感的目的就是根据y重建x。当处理图像或高维数据时应将其多维向量转换为一维长向量。若x的时域信号是非稀疏的，可将其进行某种变换使其可以稀疏表示，常用的变换有傅里叶变换、小波变换和冗余字典等。为了重建源稀疏信号，观测数据量必须满足O（KlnN），其中K为源稀疏信号非零项的个数，且矩阵φ必须满足约束等距条件［18］。对于源信号的恢复重建已有多种算法，文献［14］已证明，利用测量值通过求解最优l1－范数可重构x：

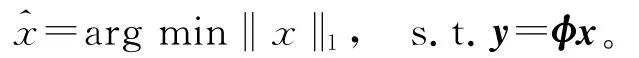
这是一个凸最优问题，可以转化为线性规划问题求解，即基追踪。其他重建算法还有匹配追踪算法、最小全变分法等。

2 压缩传感估计方法

考虑如下n维动力系统：

其中x＝（x1，x2，…，xn）∈Rn为系统状态变量，p为系统参数。

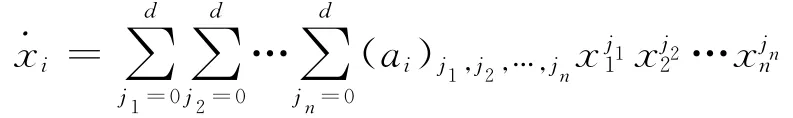
当系统在某参数p下演化时，获得第i个系统状态变量μ个测量值（xi（t1），xi（t2），…，xi（tμ）），并根据测量值求得），…，同时求得矩阵φ的μ个行向量⎿φ（t1），φ（t2），…，φ（tμ），由此获得如下等式：

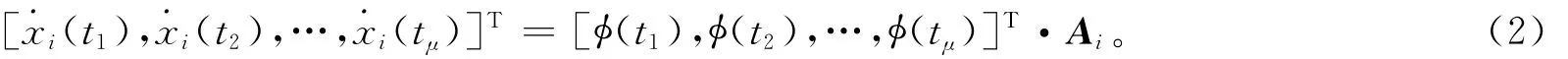
其中Ai为由系数（ai）j1，j2，…，jn组成的列向量，利用压缩传感便可以估计出Ai的值，由于Ai与系统各项存在对应关系，便可估计出系统的方程。为了满足约束等距性，将矩阵φ的每个元素除以该元素所在列的2－范数。

3 模型辨识

Lorenz系统和Rössler系统为研究非线性系统混沌现象的常用方法，是用于验证混沌控制方法的常用对象，2个系统描述如下。

Lorenz系统：

当系统参数a＝10，b＝28，c＝8／3时系统处于混沌状态。

Rössler系统：

当系统参数d＝0.2，e＝0.2，f＝5.7时系统处于混沌状态。

对于确定性系统而言，选取的幂指数越大意味着求取的向量越稀疏。以Lorenz系统取幂指数d＝3为例，在ti时刻，

共64项，由式（5）可见，对而言只有x（ti）1y（ti）0z（ti）0，x（ti）0y（ti）1z（ti）0这2项所对应的系数为非零，其余项所对应的系数皆为零；同理只有x（ti）1y（ti）0z（ti）0，x（ti）0y（ti）1z（ti）0，x（ti）1y（ti）0z（ti）1这3项为非零只有x（ti）1y（ti）1z（ti）0，x（ti）0y（ti）0z（ti）1这2项为非零。φ（ti）的系数向量为一稀疏向量，根据压缩传感原理，通过μ个的值和φ（t1），φ（t2），…，φ（tμ），可以估计出φ（ti）所对应的系数向量Ai非零系数向量同理可得。

由于未知系统方程形式，定义绝对误差与相对误差存在困难，利用估计值在某个滑动窗内波动范围小于某一小的正实数ε来确定估计是否完成，即第i个系数在某时刻τ满足

其中，j＞N且j∈｛τ－N＋1，τ－N＋2，…，τ｝，ε为估计精度。

4 负反馈混沌控制

根据测得的时间序列，按前述方法估计出系统的结构和参数，将估计得到的动力学方程按照文献［3］的控制策略将混沌系统控制到设定目标上。

为了使2个系统都稳定在x＝p1，y＝p2点上，

Lorenz控制输入取为

Rössler控制输入取为

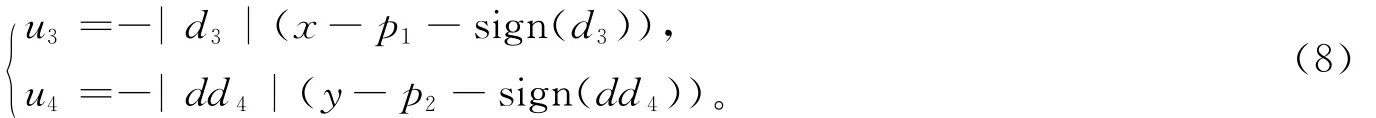
根据稳定性条件＝0，参数d1，d2，d3，d4分别为

为了将系统控制到任意周期轨道上，用一个外部振荡器产生正弦信号x＝p1＝rsin（ωt），y＝p2＝cos（ωt），代入式（9）、式（10）得到相应控制参数，将式（9）、式（10）代入式（7）、式（8）得到控制输入。

5 仿真实验

Lorenz系统的结构和参数辨识，取最大幂指数d＝3，共有64个系数，步长为0.01时，系数估计值随时间序列向量个数的关系如图1—图3所示，可以看出，非零项快速收敛到其真实值，零项收敛到零。而利用递推最小二乘法估计的结果收敛速度很慢且有较大的稳态误差，如图4－图6所示。根据非零系数与非零项的对应关系，便估计出了系统的动力学方程。

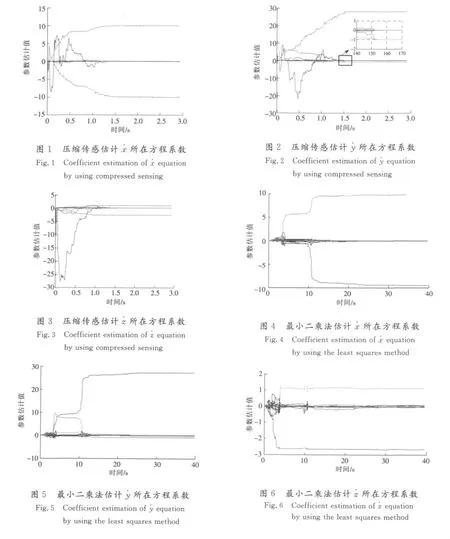
取初始值不同，完成辨识的速度也不同。对Lorenz系统而言，当步长取0.01，初始值选择为x（0）＝2.5，y（0）＝－1.8，z（0）＝0.5时，按式（6）条件需要304个点才能完成估计，相同步长下初始值选择为x（0）＝0.01，y（0）＝0.03，z（0）＝0.05时，只需207个点就可以完成估计。如果将估计参数按式（6）中ε精度舍入，则估计得到的方程就是Lorenz系统的实际方程。

当取p1＝2.5，p2＝－1时，第20s时施加控制，施加控制后系统变量很快被控制到了固定点上，而当第40s时结构发生了变化，由Lorenz系统变为Rössler系统，重新启动系统辨识，经过一段时间后得到了时间序列新的动力学方程。在第60s时再一次施加控制，经过短暂几秒系统重新回到目标点（x，y）＝（p1，p2）上，如图7所示。将系统控制到产生周期振荡上，取r＝5，ω＝3，如图8所示，也得到了良好的效果。

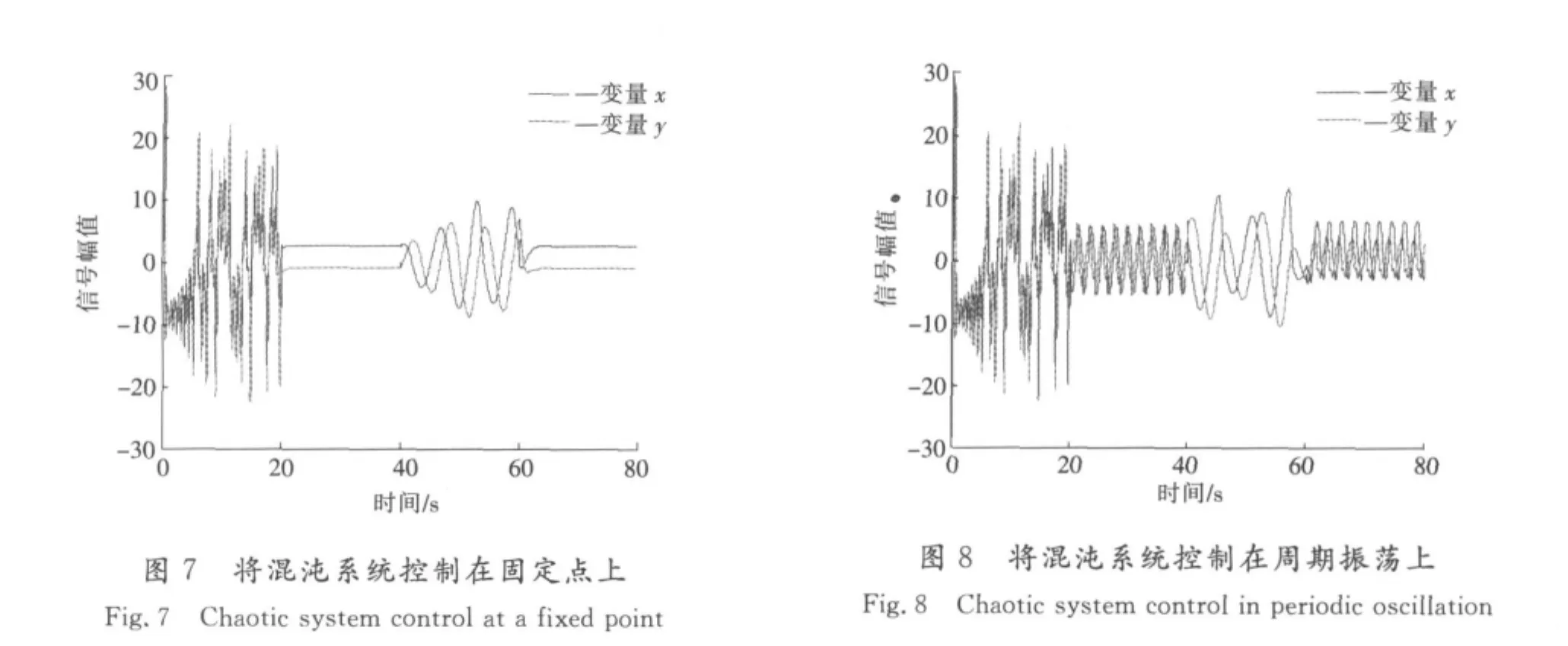
对于系统结构的辨识其实收敛速度非常快，图8中从约第19s开始辨识，到第20s时已达辨识精度要求。辨识完成后开始实施控制，第60s只是施加控制的时间，只需不到2s便可辨识出新系统，而并非经过20s才能将系统辨识出来，图8只是为了显示更直观一些。

当系统结构不变而参数发生变化时，如定点控制中，Lorenz系统参数b由28变成100时，控制系统会收敛到另一点上，由于不满足约束等距性，这时利用压缩传感不能估计出系统方程。解决办法是零控制输入为零，让系统回到混沌状态，重新辨识参数后再施加控制。

6 结 论

主要研究了在未知混沌系统方程下仅通过时间序列控制混沌的方法，将系统方程辨识方法应用于混沌自适应控制的辨识过程中。相比于利用离线逼近方法控制混沌，本方法是一种在线的辨识；相比于无模型混沌控制，本方法是一种“已知”系统模型的混沌控制，可以实现输出预测，避免边界危机；相比于最小二乘法估计系统方程和结构，本方法收敛速度很快且几乎没有稳态误差。提出的基于压缩传感的混沌自适应控制方法实现了在未知混沌系统方程情况下，首先利用输出时间序列估计出了Lorenz和Rössler系统的方程和参数，并使用负反馈控制将混沌系统成功控制在某一固定点或周期振荡上，系统方程辨识过程和混沌控制过程均有很快的收敛速度。该控制方法在保密通信、生物工程、控制工程等领域有潜在的应用，为混沌控制提供了一个新的思路。

［1］ EDWARD O，GREBOGI C，YORKE J A.Controlling chaos［J］.Physical Review Letters，1990，64（11）：1 196－1 199.

［2］ QU Zhi－lin，HU Gang，MA Ben－kun.Controlling chaos via continuous feedback［J］.Physics Letters A，1993，178（3／4）：265－270.

［3］ 罗晓曙，刘慕仁，方锦清，等.一种基于系统变量的线性和非线性变换实现混沌控制的方法［J］.物理学报（Acta Physica Sinica），2000，49（5）：849－853.

［4］ 关新平，彭海朋，李丽香，等.Lorenz混沌系统的参数辨识与控制［J］.物理学报（Acta Physica Sinica），2001，50（1）：26－29.

［5］ HUANG De－bin.Adaptive－feedback control algorithm［J］.Physical Review E，2006，73：1－8.

［6］ DITTO W L，RAUSEO S N，SPANO M L.Experimental control of chaos［J］.Physical Review Letters，1990，65（26）：3 211－3 214.

［7］ ALSING P M，GAVRIELIDES A，KOVANIS V.Using neural networks for controlling chaos［J］.Physical Review E，1994，49（2）：1 225－1 231.

［8］ KOBRAVI H R，ERFANIAN A.A decentralized adaptive robust method for chaos control［J］.Chaos，2009，19：1－7.

［9］ GOUESBET G，LETELLIER C.Global vector field reconstruction by using a multivariate polynomial L2approximation on nets［J］.Physical Review E，1994，49（6）：4 955－4 972.

［10］ BEZRUCHKO B P，SMIRNOV D A.Constructing nonautonomous differential equations from experimental time series［J］.Physical Review E，2000，63：1－7.

［11］ WANG Wen－xu，YANG Rui，LAI Ying－cheng，et al.Predicting catastrophes in nonlinear dynamical systems by compressive sensing［J］.Physical Review Letters，2011，106：1－4.

［12］ DONOHO D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1 289－1 306.

［13］ CANDÈS E J.Compressive sampling［A］.Proceedings of International Congress of Mathematicians［C］.Madrid：European Mathematical Society Publishing House，2006.1 433－1 452.

［14］ CANDÈS E，ROMBERG J，TAO T.Robust uncertainty principles exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）：489－509.

［15］ 李树涛，魏 丹.压缩传感综述［J］.自动化学报（Acta Automatica Sinica），2009，35（11）：1 369－1 377.

［16］ DUARTE M F，DAVENPORT M A，TAKHAR D，et al.Single－pixel imaging via compressive sampling［J］.IEEE Signal Processing Magazine，2008，25（2）：83－91.

［17］ TAUBOCK G，HLAWATSCH F.A compressed sensing technique for ofdm channel estimation in mobile environments exploiting channel sparsity for reducing pilots［A］.The IEEE International Conference on Acoustics，Speech，and Signal Processing［C］.Las Vegas：IEEE，2008.2 885－2 888.

［18］ CANDÈS E，TAO T.Decoding by linear programming［J］.IEEE Transactions on Information Theory，2005，51（12）：4 203－4 215.

［19］ 陈予恕，梁建术.自适应延时反馈控制混沌方法［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2006，27（4）：267－271.

［20］ 梁建术，李 兰.一类参数不确定Rössler系统的自适应反推混沌控制［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2009，30（4）：285－289.

Adaptive control of chaos based on compressive sensing

ZHAO Ying－bao1，HUANG Li－min2
（1.College of Electrical Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China；2.Modern Education Technology Center，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

An adaptive chaos control method is proposed，using compressed sensing to identify equations and parameters of chaotic systems based only on the output time series，and using negative feedback control of chaotic system to set goals.Lorenz and the Rössler system is used to illustrate the identfication and control of equations and parameters of the time－varying structure system.First the Lorenz system is controlled to a fixed point or periodic oscillations.When the structure changes to Rössler，the new structure and its parameters is recognized，and the system retruns to the control objectives again.The results show that，compared to least－squares method，the method can be realized with less data，while the model structure and parameters are estimated with high accuracy.Then negative feedback can be used to control rapidly the system to the set goals.

compression sensing；negative feedback control；model estimation；chaos control；parameter estimation

TP273＋.2

A

1008－1542（2012）03－0248－05

2011－12－24；责任编辑：陈书欣

赵英宝（1972－），男，河北张家口人，讲师，主要从事电力电子、模糊控制方面的研究。