四阶非局部边值问题方程组正解的存在性

索秀云，郭少聪，张继叶，郭彦平

（河北科技大学理学院，河北石家庄 050018）

四阶非局部边值问题方程组正解的存在性

索秀云，郭少聪，张继叶，郭彦平

（河北科技大学理学院，河北石家庄 050018）

利用锥上的Krasnoselskii不动点定理研究了一类具有积分边界条件的四阶非局部微分方程组边值问题正解的存在性。通过在Banach空间定义一个全连续的算子，得到了它至少存在1个正解的充分条件。

正解；非局部边值问题；Krasnoselskii不动点定理

基于四阶线性微分方程边值问题在物理方面的背景，文献［1］—文献［7］分别用Leray－Schauder度理论、不动点定理、上下解的方法证明了四阶方程解的存在性。

在文献［1］中，作者主要研究了下列非局部边值问题：

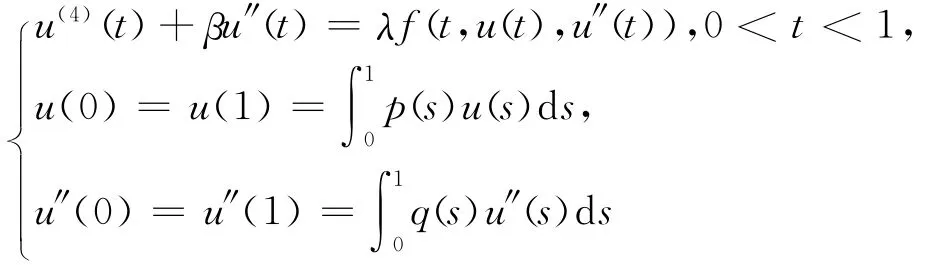
正解的存在性。受上述文章的启发，笔者主要考虑下列非局部边值问题方程组：正解的存在性。本文假设如下条件成立：

1 主要引理

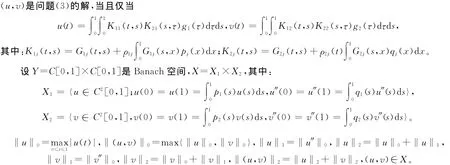
引理2 （X，‖（u，v）‖2）是Banach空间。

证明 由文献［1］中引理2.1知：（X1，‖u‖2），（X2，‖v‖2）都是Banach空间，故（X，‖（u，v）‖2）也是Banach空间。

引理3［5］假设A1），A2）成立，那么有

2 主要结论

设Kij，G2j，ρ2j，c2j，θj如第2部分所定义，下面介绍一些记法如下：

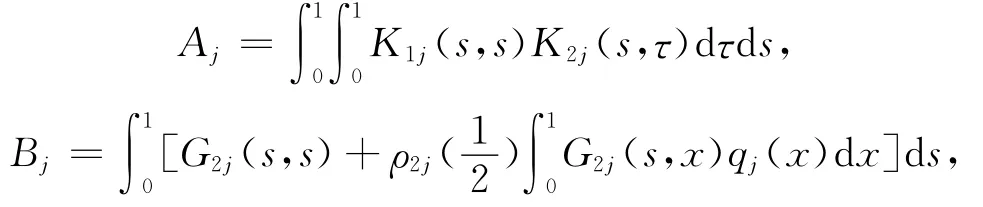
之一成立时，其中i＝1，2，则问题（1）至少存在1组正解。

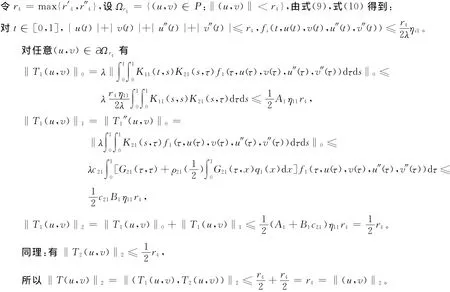
由Krasnoselskii不动点定理ii）知，问题（1）至少存在1组正解。

［1］ BAI Z B.Positive solutions of some nonlocal fourth－order boundary value problem［J］.Applied Mathematics and Compution，2010，215：4 191－4 197.

［2］ BAI Z B.The method of lower and upper solution for a bending of an elastic beam equation［J］.J Math Anal Appl，2000，248：195－202.

［3］ BAI Z B.The method of lower and upper solution for some fourth－order boundary value problems［J］.Nonlinear Anal，2007，67：1 704－1 719.

［4］ FENG H Y，JI D H，GE W G.Existence and uniqueness of solutions for a fourth－order boundary value problem［J］.Nonlinear Anal，2009，70：3 561－3 566.

［5］ LI Y X.Positive solutions for nonlocal boundary value problems［J］.Nonlinear Anal，2003，54：1 069－1 078.

［6］ YAO Q L.Local existence of multiple positive solutions to a singular cantilever beam eqution［J］.J Math Anal Appl，2010，363：138－154.

［7］ ZHAO J F，GE W G.Positive solutions for a higher－order four－point boundary value problem with ap－Laplacian［J］.Comput Math Appl，2009，58：1 103－1 112.

Existence of positive solutions for nonlocal forth order boundary value problem systems

SUO Xiu－yun，GUO Shao－cong，ZHANG Ji－ye，GUO Yan－ping
（College of Sciences，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

By using Krasnoselskii fixed point theorem in a cone，the existence of positive solutions for nonlocal forth order boundary value problem systems with integral boundary conditions is studied.By defining a completely continuous operator in a Banach space，the sufficient condition under which the above problem has at least one positive solution is derived.

positive solution；nonlocal boundary value problem；Krasnoselskii fixed point theorem

O175.8

A

1008－1542（2012）03－0197－05

2011－10－10；责任编辑：张 军

国家自然科学基金资助项目（10971045）；河北省自然科学基金资助项目（A2009000664）

索秀云（1954－），女，河北磁县人，副教授，主要从事概率统计与应用微分方程方面的研究。