带2个参数的二阶脉冲微分方程3点边值问题的正解
郭少聪,郭彦平,张素芬
(1.河北科技大学理学院,河北石家庄 050018;2.石家庄信息工程职业学院,河北石家庄 050035)
带2个参数的二阶脉冲微分方程3点边值问题的正解
郭少聪1,郭彦平1,张素芬2
(1.河北科技大学理学院,河北石家庄 050018;2.石家庄信息工程职业学院,河北石家庄 050035)
利用锥上的Krasnoselskii不动点定理,讨论了带有2个参数的二阶脉冲微分方程3点边值问题正解的存在性和不存在性。通过定义合适的积分算子,给出了该问题有1个正解或2个正解以及不存在正解的充分条件。
脉冲微分方程;正解;Krasnoselskii不动点定理
1 预备知识
脉冲微分方程描述的是事物在发展过程中的某一时刻某一状态发生突变,脉冲微分方程已经成为了微分方程中一个非常重要的研究领域。比如,边值问题作为脉冲微分方程的一个重要分支,已经引起了很多学者的关注,并激发了他们极大的研究兴趣[1-6]。常微分方程边值问题的研究中有很多关于多点边值问题的研究著作,但是仅有少量论文研究带参数的二阶非线性脉冲微分方程边值问题[7]。
YAN在文献[6]中利用锥上的锥拉伸和锥压缩不动点定理研究了带2个参数的周期泛函脉冲微分方程的周期正解的存在性以及不存在性。文献[3]通过运用相同的定理得到了二阶脉冲微分方程3点边值问题正解的存在性的结论:


其中,f∈C([0,+∞),[0,+∞)),α∈C(J,(0,1]),对t∈J,t≤α(t)≤1,β>0,η∈(0,1),a(t)∈C(J,[0,+∞)),且1-βη>0。
基于以上研究,笔者主要研究带2个参数的二阶脉冲微分方程3点边值问题,即


本文中用到的主要定理是锥上的krasnoselskii不动点定理[7]。
定理1 设X是Banach空间,K是X上的一个锥,设Ω1,Ω2分别是X的有界开子集,θ∈Ω1⊂⊂Ω2,若算子T:K∩(\Ω1)→K是全连续算子,且满足下面2个条件之一:
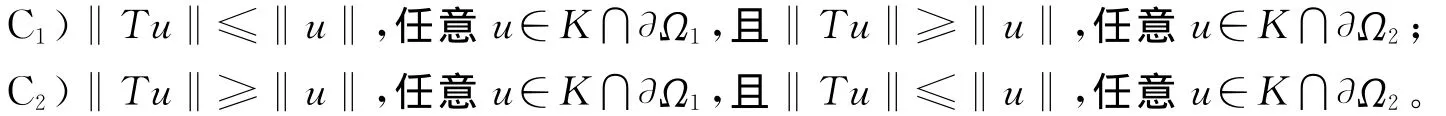
那么,A在K∩\Ω1)中至少存在1个不动点。
2 相关引理
在这一部分,给出一些在证明过程中必要的引理。
引理1 令η∈(0,1),1≠βη,那么对y∈C[0,1],问题
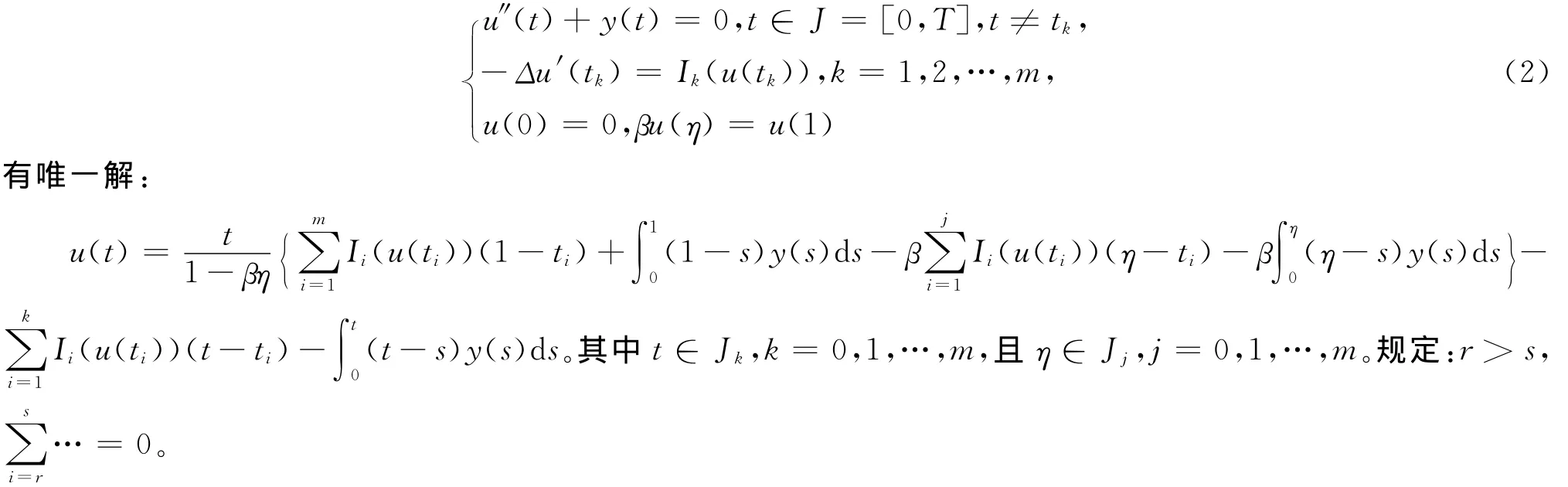
引理2[3]如果条件H4)成立,设Ii≥0,i=0,1,…,m且y∈C(J,R+),那么式(2)的唯一解在J上满足的条件u(t)≥0。
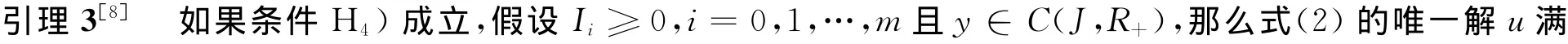

3 主要结论
定理2 假设条件H1)-H4)成立,且f0,f∞都是正数,且满足

式中:η∈Jj;j=0,1,…,m;i=0,1,…,m。那么式(1)至少有一个正解。
证明 根据式(4)选择ε>0,使得:







[1] BAINOV D D,SIMEONOV P S.Impulsive Differential Equations:Periodic Solutions and Applications[M].Harlow:Longman Science and Technical,1993.
[2] LI J,HUA J.Multiple positive solutions for a second-order three-point boundary value problem[J].Appl Math Comput,2006,182:258-268.
[3] JANKOWSKI T.Positive solutions of three-point boundary value problems for second order impulsive differential equations with advanced arguments[J].Appl Math Comput,2008,197:179-189.
[4] GUO D,LIU X.Multiple positive solutions of boundary value problems for impulsive differential equations[J].Nonlinear Analysis,1995,25:327-217.
[5] LIU X,QIU J,GUO Y.Three positive solutions for second-order m-point boundary value problems[J].Appl Math Comput,2004,156:733-742.
[6] YAN J.Existence of positive periodic solutions of impulsive functional differential equations with two parameters[J].J Math Anal Appl,2007,327:854-868.
[7] GUO D,LAKSHMIKANTHAM V.Nonlinear Problems in Abstract Cones[M].San Diego:Academic Press,1998.
[8] MA R.Positive solutions of a nonlinear three-point boundary value problem[J].Electronic Journal of Differential Equations,1999,34(4):1-8.
Positive solutions to three-pointboundary value problems for second order impulsive differential equations with two parameters
GUO Shao-cong1,GUO Yan-ping1,ZHANG Su-fen2
(1.College of Sciences,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China;2.Shijiazhuang Information Engineering Vocational College,Shijiazhuang Hebei 050035,China)
In this paper,the Krasnoselskii's fixed-point index theorem is employed in a cone to study the existence and non-existence of positive solutions to the second order impulsive functional differential equations with two parameters.By defining integral operators,sufficient conditions under which the above problem has at least one or two positive solutions or has no positive solution are put forward.
impulsive differential equation;positive solution;Krasnoselskii's fixed-point theorem
O175.8
A
1008-1542(2012)02-0097-06
2011-09-29;责任编辑:张 军
国家自然科学基金资助项目(10971045);河北省自然科学基金资助项目(A2009000664,A2011208012)
郭少聪(1965-),男,河北井陉人,讲师,主要从事应用微分方程及优化控制方面的研究。

