带有积分边值条件的三阶边值问题正解的存在性
刘玉敬,郭少聪,郭彦平
(1.河北科技大学理学院,河北石家庄 050018;2.河北科技大学电气信息学院,河北石家庄 050018)
带有积分边值条件的三阶边值问题正解的存在性
刘玉敬1,郭少聪1,郭彦平2
(1.河北科技大学理学院,河北石家庄 050018;2.河北科技大学电气信息学院,河北石家庄 050018)
应用特征值准则研究了一类三阶带有积分边值条件边值问题正解的存在性,其中非线性项f:[0,1]×[0,∞)→[0,∞)满足Caratheodory条件。在赋予非线性项一定条件下,得到该边值问题至少存在3个正解的充分条件。
特征值准则;格林函数;正解;边值问题;积分边值条件
近几年,从研究二阶带有一般边值条件的微分方程多重正解存在性到偶数阶的边值问题正解的存在性,文献[1]-文献[3]都应用了算子特征值和不动点指数性质的方法,给出了一些新的结论。
物理和数学中常常出现一类带有积分边值条件的边值问题,但是由于Green函数难构造,有关该问题的研究成果较少。2011年,ZHAO等研究了带有积分边值条件的三阶边值问题[4]:
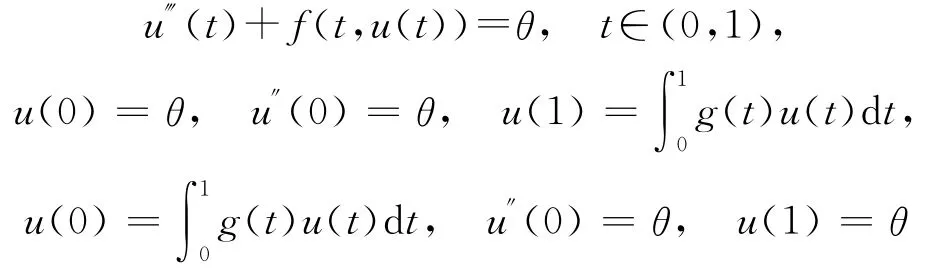
解的存在与不存在性。笔者利用算子特征值的方法研究带有积分边值条件的三阶微分方程
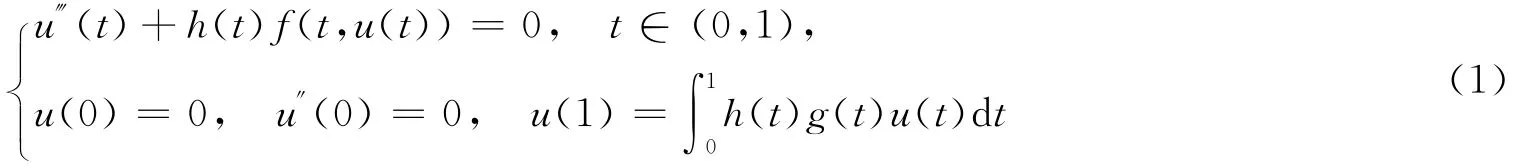
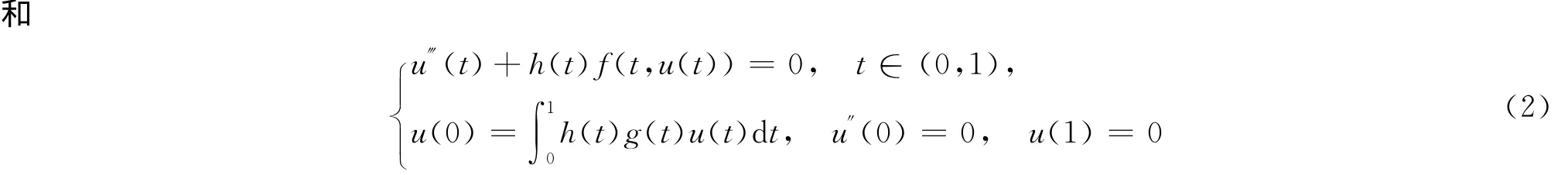
多重正解的存在性,其中f:[0,1]×R+→R+的函数。本文的结果补充和完善了文献[4]的结论。
本文总是假设下列条件成立。

1 基本引理
定义1[1]P为Banach空间X中一个锥,如果X中每个元素x=x+-x-,其中x+,x-∈P,则P为再生锥。
引理1 (Krein-Rutman)[5]K为实Banach空间X的一个再生锥,令L:X→X为紧线性算子且L(K)⊂K。设r(L)为L的谱半径,如果r(L)>0,那么存在φ1∈K\{0},使得Lφ1=r(L)φ1。
引理2[6]X是一个Banach空间,P为X中锥,Ω(P)为P中一个有界开子集,设A:(P)→P是一个全连续算子。那么下列结论成立:
1)如果存在u0∈P\{0},对∀u∈∂Ω(P)和λ≥0,都有u≠Au+λu0。那么不动点指数i(A,Ω(P),P)=0;
2)当0∈Ω(P),对∀u∈∂Ω(P)和λ≥1都有Au≠λu。那么不动点指数i(A,Ω(P),P)=1。

易证P是X中的再生锥,K为X中锥;Pr,Kr为P中一个有界开子集。


2 主要结论


3 重要定理


则边值问题(1)至少存在3个非零正解,满足:ρ<‖u1‖<ρ2<‖u2‖<ρ1<‖u3‖≤r。
证明 设0<ρ<min{ρ0,ρ2},由引理7和式(12)得:i(A,Pρ,P)=1。由定理1已证i(A,Kρ1,K)=1,i(A,Kρ2,K)=0。设r>max{ρ1,r0},由引理10和式(11),则或者i(A,Kr,K)=0,或者存在u∈∂Kr,Au=u。由不动点指数性质,边值问题(1)至少存在3个非零正解u1,u2,u3∈K,满足:ρ<‖u1‖<ρ2<‖u2‖<ρ1<‖u3‖≤r。
注:将算子A换成A*,同样的证明方法可以得到边值问题(2)至少存在3个非零正解的定理。
[1] WEBB J R L,LAN K Q.Eigenvalue criteria for existence of multiple positive solutions of nonlinear boundary value problems of local and nonlocal type[J].Topological Methods in Nonlinear Analysis,2006,27:91-115.
[2] JIANG Wei-hua.The existence of positive solutions for second-order multi-point BVPs with the first derivative[J].Journal of Computational and Applied Mathematics,2009,225:387-392.
[3] JIANG Wei-hua.Eigenvalue criteria for existence of multiple positive solutions of high-order nonlinear BVPs[J].Nonlinear Analysis,2008,69:295-303.
[4] ZHAO J F,WANG P G,GE W G.Existence and nonexistence of positive for a class of third order BVP with integral boundary conditions in banach spaces[J].Commun Nonlinear Sci Numer Simulat,2011,16(1):402-413.
[5] NUSSBAUM R D.Eigenvectors of nonlinear positive operators and the linear Krein-Rutman theorem[J].Lecture Notes in Math,1981,886:309-330.
[6] GUO D,LAKSHMIKANTHAM V.Nonliear Problems in Abstract Cones[M].San Diego:Academic Press,1988.
Existence of positive solutions of the third order boundary value problems with integral boundary conditions
LIU Yu-jing1,GUO Shao-cong1,GUO Yan-ping2
(1.College of Sciences,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China;2.College of Electrical Engineering and Information Science,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China)
By using eigenvalue criteria,the existence of positive solutions to the boundary value problems with integral boundary conditions is considered,where the nonlinear termf:[0,1]×[0,∞)→[0,∞)satisfies Caratheodory conditions.The existence of at least three positive solutions is proved for the boundary value problems when the nonlinear term meets some certain conditions.
eigenvalue criteria;Green's function;positive solution;boundary value problem;integral boundarycondition
O175
A
1008-1542(2012)02-0093-04
2011-09-26;责任编辑:张 军
国家自然科学基金资助项目(10971045);河北省自然科学基金资助项目(A2009000664)
刘玉敬(1976-),女,河北唐山人,讲师,硕士,主要从事微分方程方面的研究。

