三维感应测井数值计算与理论分析
张国艳,肖加奇,郝永杰
(中国石油集团长城钻探工程有限公司,北京100176)
三维感应测井数值计算与理论分析
张国艳,肖加奇,郝永杰
(中国石油集团长城钻探工程有限公司,北京100176)
研究了三维感应测井仪器在均匀、无限大、横向各向同性(TI)导电地层中的响应,分析了井眼倾角、水平电导率、垂直电导率、工作频率等因素对接收线圈系感应电动势的影响。趋肤效应对XX/YY方向感应电动势的影响比ZZ方向显著;垂直井时,水平方向电导率可通过ZZ感应电动势求解;垂直电导率可通过XX/YY方向感应电动势和求得的联合计算求解。倾斜角可通过交叉耦合电动势计算。在低频近似条件下,计算证明了可由三维感应测井响应提取地层各向异性电导率以及井眼倾角等信息,为三维感应测井资料解释奠定了基础。
三维感应测井;各向同性;横向;数值计算;理论分析
0 引 言
据估计,世界上大约有30%的油气储存于砂泥岩薄交互层中[1],现有的感应测井仪器由于纵向分辨率还不够高,往往将这种薄交互储层误认为是高含水饱和度层而漏掉[2]。对水平井、斜井所体现出的宏观各向异性地层的测量,传统的感应测井仪器不能解决。三维感应测井仪器是由3个彼此垂直的发射线圈和与之平行的3个接收线圈组成,可以从三维角度识别地层特性,对薄储层、复杂储层的探测具有先天优势。贝克-阿特拉斯公司和壳牌公司联合开发的三维探测仪3DEX[3-5]以及斯伦贝谢公司开发的三轴感应测井仪器[6]的试验已显示出三维感应测井在探测各向异性油藏方面的应用潜力。
数值计算和理论分析对三维感应测井仪器的设计、响应特征的分析和数据反演处理技术的开发具有重要意义。目前国外已有大量文献阐述了三维感应测井的基础理论及数值计算[7-11],但是国内详细阐述这方面的文章却很少。本文研究了三维感应测井仪器在均匀、无限大、横向各向同性(TI)导电地层中的响应,分析了井眼倾角、横向电导率、垂直电导率、趋肤效应等因素对接收线圈系感应电动势的影响。
1 三维感应测井仪器基本理论
三维感应测井仪器的线圈系结构(见图1)由3个中心共点的、彼此垂直的发射线圈Tx、Ty、Tz和与其平行的3个接收线圈Rx、Ry、Rz以及3个屏蔽线圈Bx、By、Bz组成。当发射线圈系向周围发射正弦交流电时,在介质中产生交变电磁场(一次磁场),根据电磁感应原理,在该磁场中的接收线圈和屏蔽线圈将产生感应电动势。
为了抵消发射线圈在接收线圈中产生的直接耦合分量引入屏蔽线圈。所谓直接耦合是指发射信号在不经过地层的情况下,由于磁通的闭合特性在接收线圈中直接引起的感应信号。屏蔽线圈与接收线圈的绕线方向相反,匝数不等,在空气中屏蔽线圈和接收线圈中产生的直耦电动势相互抵消。
当发射线圈系向周围发射正弦交流电时,可同时测量接收线圈系上磁场(或感应电动势)张量的9个分量。磁场强度张量H表示成
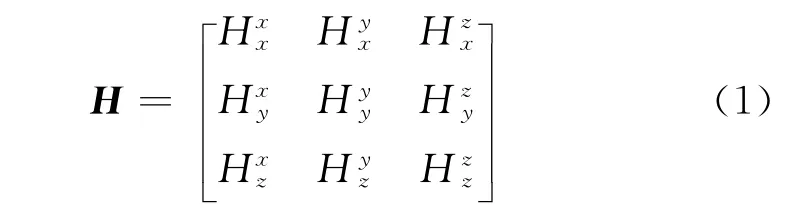
其中,Hyx表示由x方向发射、y方向接收产生的磁场强度,其他分量定义依此类推。
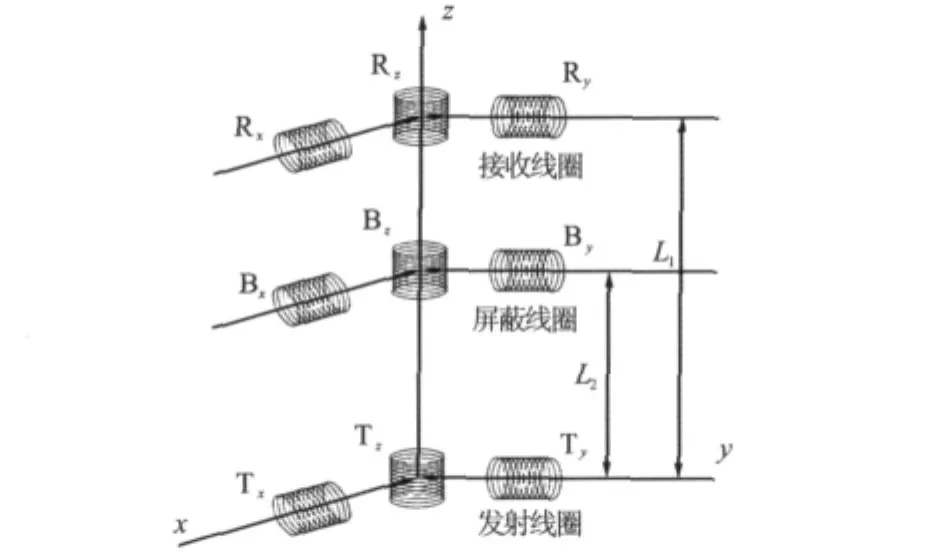
图1 线圈系结构
计算过程中线圈等效为点磁偶极子,数学模型见图2所示。许多地层(如砂泥岩薄交互层)表现为宏观横向各向同性(TI)地层[12],也称为单轴各向异性地层,其水平(横向)电导率σh和垂直(纵向)电导率σv不相等,所以TI介质的电导率在地层坐标系中可表示为对角矩阵
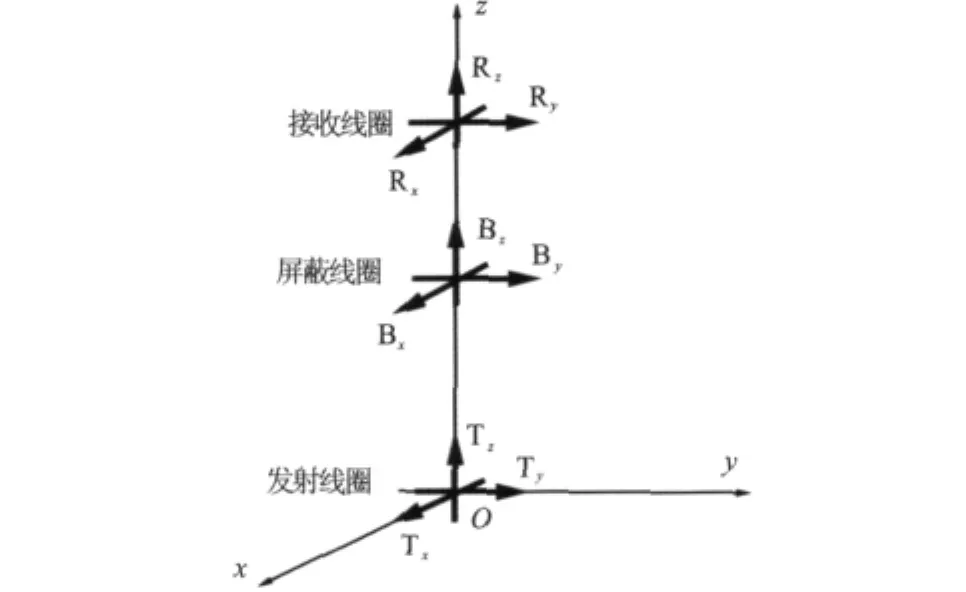
图2 数学模型
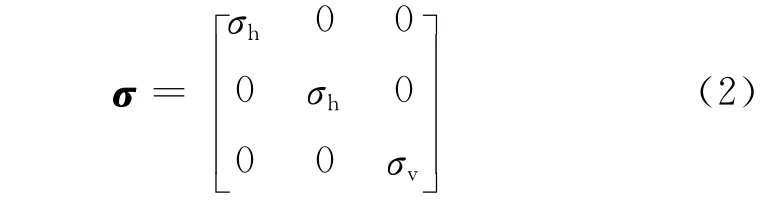
Zhdanov等[10]在Moran等[11]工作的基础上推导出三维感应测井仪器在无限大TI介质中响应的解析表达式。发射线圈为单位磁矩时,地层坐标系下的磁场强度张量为
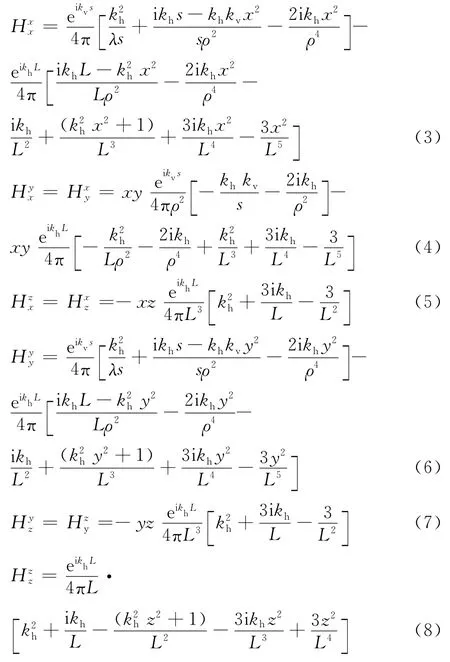
考虑到测井仪器的倾斜,需要引入仪器坐标系,设地层参考坐标系为OXYZ,沿X、Y、Z方向上的电导率分别为σh、σh、σv,仪器坐标系为X′Y′Z′(见图3)。图3中α为井眼倾角,定义为地层坐标系的Z轴和仪器坐标系Z′间夹角;β为仪器方位角,定义为仪器在XY平面的投影与X轴之间的夹角。式(3)至式(8)为基于地层坐标系的磁场计算公式,通过坐标变换矩阵R可得到仪器坐标系下的磁场强度H′。

图3 仪器坐标系和地层坐标系
坐标变换矩阵R可表示成
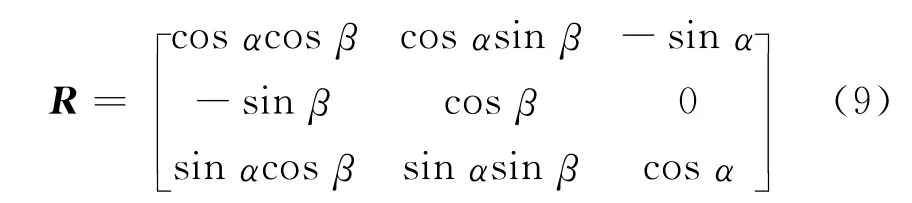
设地层坐标系下发射线圈的磁矩M=(Mx,My,Mz)T,仪器坐标系下发射线圈的磁矩M′=(M′x,M′y,M′z)T。当发射线圈为单位磁矩时,地层坐标系下磁场强度为H,公式见式(3)至式(8)。当发射线圈磁矩为M时,地层坐标系下磁场强度为HM,此时

坐标变换后,
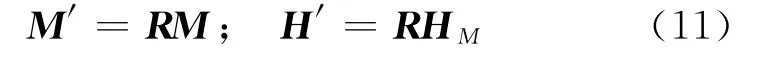
把式(10)代入式(11),整理得
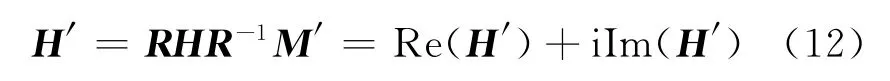
其中,R-1为R的逆矩阵;Re(H′)、Im(H′)分别为仪器坐标系下磁场强度的实部和虚部。接收线圈在仪器坐标系的感应电动势
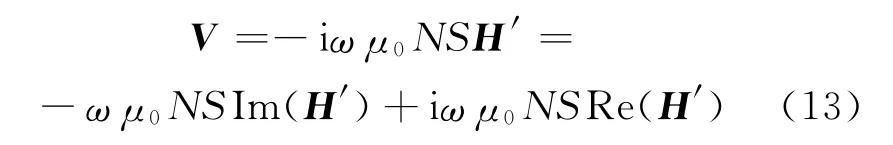
式(13)中,S为接收线圈的面积;N为接收线圈的匝数。感应电动势的实部与仪器坐标系下磁场强度的虚部Im(H′)成正比。考虑到接收线圈与屏蔽线圈绕线方向相反,所以接收线圈系在仪器坐标系的感应电动势

式中,Vijr、Vijb分别为接收线圈和屏蔽线圈感应电动势。本文只计算接收线圈系感应电动势的实部[10]。
2 数值计算及分析
利用程序对三维感应测井仪器的响应进行了数值计算,并用理论公式和低频近似公式进行了分析。
线圈参数:发射线圈磁矩Mx=My=Mz=1,发射线圈与接收线圈间距离L1=20in*,发射线圈与屏蔽线圈间距离L2=15in,接收线圈X/Y/Z方向匝数Nr=64匝,屏蔽线圈X/Y/Z方向匝数Nb=27匝,接收线圈和屏蔽线圈X/Y/Z方向的面积均为Sr=Sb=0.03m2;工作频率范围20~220kHz。
地层参数:无限大、均匀、横向各向同性地层,水平方向电导率σh和垂直方向电导率σv的变化范围0.01~10S/m。
2.1 水平电导率和垂直电导率的影响
工作频率f=20kHz,α=0(垂直井),β=0,改变水平方向电导率σh(σv=0.01S/m)和垂直方向电导率σv(σh=10S/m)进行了数值计算,结果如图4所示。接收线圈系感应电动势只有3个主分量不为0,且Vxx=Vyy,实际独立的只有2个变量。随着σh和σv的增加,Vxx呈增加趋势;Vzz随着σh的增加而增加,随着σv的增加数值保持不变。
感应电动势表达式[6,13]
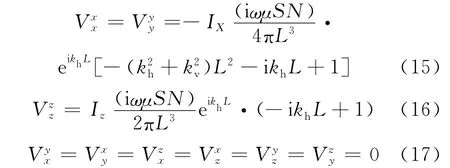
根据式(15)至式(17)得到电动势3个主分量不为0,Vxx=Vyy;Vzz只与σh有关,与σv无关;而Vxx、Vyy与σh和σv两者都有关,数值计算结果和理论分析一致。且σh可根据式(16)计算得到,代入式(15),可求解σv。
考虑井眼一般倾斜情况(α=60°),其他条件同上,改变σh和σv进行计算,得到结果如图5所示。3个主分量和XZ/ZX方向交叉分量不为0;Vxx≠ Vyy,Vxz=Vzx;Vzz和Vxz数值都逐渐增加但是符号相反,Vxz数值为负说明此时感应磁场方向和发射电流方向相差180°。

2.2 井眼倾角的影响
计算时工作频率f=20kHz;β=0;σh=1;σv=0.1。改变井眼倾角α得到接收线圈系感应电动势变化如图6所示。Vxz=Vzx,其数值先增加后降低;Vzz随着α增加而降低;Vxx、Vyy随着α增加而增加。当β=0时,低频磁场近似公式[10]
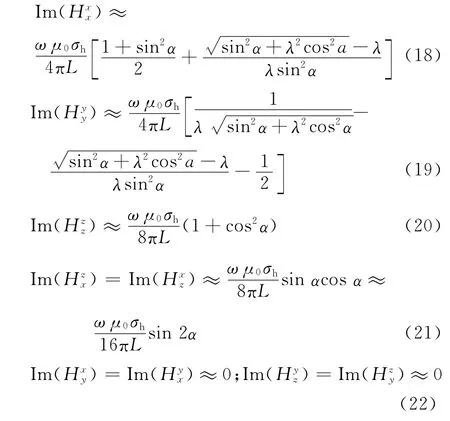
根据式(21)可以得到Vxz=Vzx,且随着α增加数值近似正弦变化,在α=45°时达到峰值;井眼倾角α可通过Vxz/Vzx计算得到。根据公式(20),可以看出Vzz与(1+cosα2)成正比。
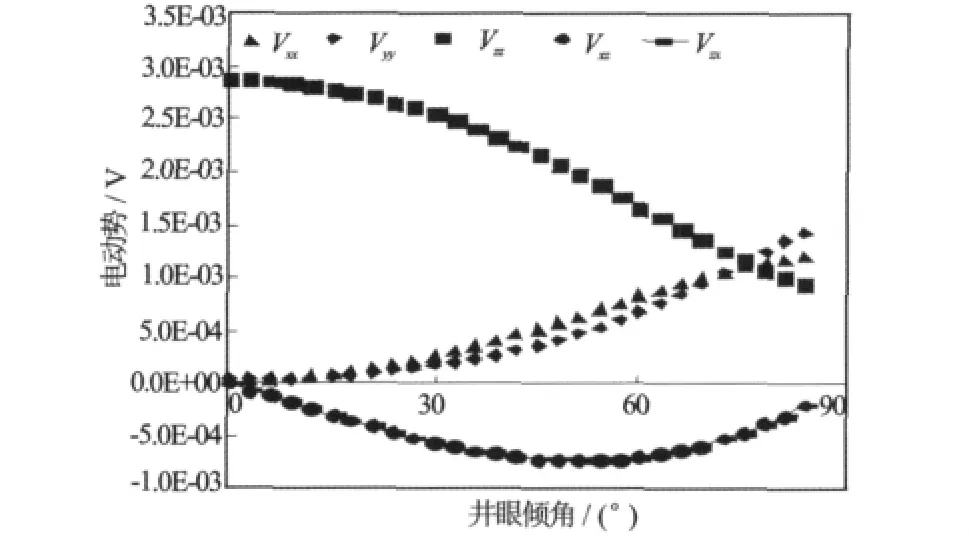
图6 感应电动势随井眼倾斜角的变化
2.3 趋肤效应的影响
研究趋肤效应现象主要是计算感应电动势受电导率和频率的影响。考虑电导率变化时电动势的影响见图5所示。随着σh和σv增加,Vxx、Vyy的非线性比Vzz严重,即趋肤效应对XX/YY感应电动势的影响显著比ZZ方向强,趋肤效应的影响可以从式(15)至式(16)分析,Vyy和Vxx比Vzz多了一项[-(k2h+k2v)L2]eikhL,所以趋肤效应对XX/YY感应电动势的影响比ZZ方向显著。
改变工作频率计算接收线圈组感应电动势时,α=60°,β=0,σh=1,σv=0.1,结果见图7。Vxz=Vzx;随着频率增加,可以看出趋肤效应对XX/YY感应电动势的影响比ZZ方向显著,趋肤效应的影响可以通过公式(15)至式(16)分析。

图7 感应电动势随频率的变化
3 结束语
研究了三维感应测井仪器在均匀、无限大、横向各向同性(TI)导电地层中的响应,分析了井眼倾角、横向电导率、垂直电导率、趋肤效应等因素对接收线圈系感应电动势的影响。垂直井,水平方向电导率σh可通过ZZ感应电动势求解;垂直电导率σv可通过XX/YY方向感应电动势和求得的σh联合计算求解。倾斜角α可通过交叉耦合电动势Vxz/Vzx计算。趋肤效应对XX/YY方向感应电动势的影响比ZZ方向显著,这在仪器设计时应考虑。
[1] 党瑞荣,秦瑶,谢雁,等.三维感应测井系统研究[J].石油地球物理勘探,2006,41(4):484-488.
[2] Forgang,Stanislav,Fanini,et a1.Method and Apparatus for Transverse Electromagnetic Induction Well Logging:United States,5781436[P].1998.
[3] Kriegshauser B F,Fanini O N,Yu L,et al.Improved Shaly Sand Interpretation in Highly Deviated and Horizontal Wells Using Multi-component Induction Log Data[C]∥SPWLA 42nd Annual Logging Symposium,2001.
[4] Rabinovich M,Tobarovsky L,Corley B,et al.Processing Multi-component Induction Data for Formation Dips and Anisotropy[J].Petrophysics,2006,47(6):506-526.
[5] Rabinovich M,Gonfalini M,Rocque T,et al.Multicomponent Induction Logging:10Years After[C]∥SPWLA 48th Annual Logging Symposium,2007.
[6] Rosthal R,Barber T,Bonner S,et al.Field Test Results of an Experimental Fully-triaxial Induction Tool[C]∥SPWLA 44th Annual Logging Symposium,2003.
[7] Ning Yuan,Xiao Chun Nie,Richard Liu,et al.Simulation of Full Response of a Triaxial Linduction Tool in a Homogeneous Biaxial Anisotropic Formation[J].Geophysics,2010,75(2):101-114.
[8] Gianzero S,Kennedy D,Gao L,et al.The Response of Triaxial Induction Sonde in a Biaxial Anisotropic Medium[J].Petrophysics,2002,43(3):172-184.
[9] Hanming Wang,Tom Barber,Kouchiang Chen,et al.Triaxial Induction Logging:Theory,Modeling,Inversion,and Interpretation.[C]∥SPE103897,2006,12:5-7,Beijing,China.
[10]Michael Zhdanov,David Kennedy,Ertan Peksen.Foundations of Tensor Induction Well-Logging[J].Petrophysics,2001,42(6):588-610.
[11]Moran J,Gianzero S.Effects of Formation Anisotropy on Resistivity-logging Measurements[J].Geophysics,1979,44(7):1266-1288.
[12]Klein J D,Martin P R,Allen D F.The Petrophysics of Electrically Anisotropic Reservoirs[J].The Log Analyst,1997,38(3):25-36.
[13]Wang H,Barber T,Morriss C,et a1.Determining Anisotropic Formation Resistivity at Any Relative Dip U-sing a Multiarray Triaxial Induction Tool[C]∥SPE103113,2006,9:24-27.USA.
Numerical Computation and Theoretical Analysis of Three-dimensional Induction Logging Tool
ZHANG Guoyan,XIAO Jiaqi,HAO Yongjie
(CNPC Greatwall Drilling Company,Beijing 100176,China)
In this paper examined are the responses of a three-dimensional(3D)induction well logging tool in an unbounded,homogeneous,transversely isotropic conductive medium,and analyzed is the dependence of the induced potential of the receiver array with respect to the relative dip angle,the horizontal conductivity,the vertical conductivity and the frequency respectively.The results show that the induced potential in the XX/YYdirection exhibits much stronger skin effect than the induced potential in the ZZdirection.Under the low frequency approximation,we found that the horizontal conductivity,the vertical conductivity and the relative dip angle can be resolved from the three-dimensional induction instrument response in a deviated borehole as well as in a vertical borehole.This provides the basis for the data interpretation of a three-dimensional induction well logging tool.
three dimension induction logging,isotropy,transverse,numerical computation,theoretical analysis
P631.3 文献标识码:A
2011-06-01 本文编辑 李总南)
王忠义,男,1959年生,硕士,高级工程师,从事测井方法与仪器研究工作。

