抗震结构基于最大弹塑性位移耦合作用的滞回耗能谱✳

杨 伟,高 峰

(1.福建省建筑科学研究院,福建 福州 350025;2.福建省绿色建筑技术重点实验室,福建 福州 350025)

引 言

现有的抗震设计方法大多基于承载力或强度,相应的反应谱理论也无法反映地震动持时的影响或者说没有考虑结构累积滞回耗能对结构损伤的影响。为了能够反应往复地震动作用造成的结构累积耗能损伤,早在 20世纪 50年代,Housner就表达了用结构能量反应分析的观点和方法[1]。近年来,关于能量分析理论及方法又得到了更多的关注和研究。2001年 Luis D Decanini用能量理论来评估结构的抗震需求[2],引入了一个代表弹性输入能和弹塑性输入能比值的地震输入能修正系数RE和折减因子T,并通过大量的计算回归得到了考虑延性、场地类别、震中距和震级的输入能设计谱和滞回耗能与输入能比值谱。由于Park和Ang提出双参数损伤模型比较符合结构在罕遇地震作用下的破坏机理[3,4],从而围绕该损伤模型及其改进模型,研究了一些基于损伤的弹塑性反应谱或设计谱[5～7]。这些损伤谱能够综合考虑弹塑性位移和滞回耗能的耦合作用,但与本文讨论的滞回耗能谱研究的侧重点不同。关于滞回耗能谱的研究,在国内,2002年肖明葵等人计算了不同动力参数下单自由度体系弹性及弹塑性总输入能及滞回耗能[8],并得到了弹塑性体系滞回耗能谱的简化公式。2004年公茂盛等人选用美国西部加州 15次较大地震中的 266条强地震动记录[9],利用衰减关系建立了滞回耗能量谱,分析了场地条件、延性系数、震级及距离等参数对滞回耗能谱的影响。2006年程光煜等人推导了弹性多自由度系统与单自由度系统弹性地震输入能量间的关系[10]。杨晓明等人对抗震结构地震总输入能中的阻尼耗能进行了分析研究[11],讨论了不同阻尼比、不同滞回模型、地震动频谱和加速度峰值对阻尼耗能的影响。翟长海等人基于台湾集集地震的大量地震动研究了抗震结构滞回耗能特性[12],表明:场地条件、抗震结构的延性水平、周期、阻尼均是影响抗震结构滞回耗能的重要因素,而结构恢复力模型对滞回耗能的影响则可以忽略。 2008年盛明强等人比较了 Northridge与ChiChi地震的滞回耗能谱[13],并提出了滞回耗能谱简化计算公式及其相关系数。2009年滕军等人利用160条强震记录[14],计算并回归了弹性单自由度体系输入能量谱的简化计算公式。应该指出的是,以上研究除了国外研究的损伤谱之外,其余研究都仅单独考虑了能量反应,虽能够反映地震动造成累积损伤的作用,却忽略了结构最大位移首超破坏的影响,而损伤谱的研究实际上是一种强度折减系数谱或设计反应谱,与文中探讨的滞回耗能谱有着本质的区别。因此,本文基于 Park和 Ang双参数损伤模型,通过自编 DBHS(Deformation-based Hysteretic Spectrum)程序,研究基于弹塑性位移耦合作用的滞回耗能谱,具有重要意义。

1 抗震结构的能量平衡方程

在水平地震作用下,单自由度体系的运动方程可以写为

将运动方程(1)的两端对质点在(0,t)内积分,可得能量反应方程如下

上式可以简写如下

式中EK和ED分别为结构的动能、阻尼耗能;EY为结构弹性变形能ES与非弹性累积滞回耗能EH之和,也有人称之为系统总的变形能;EI为地震动总输入能,式(3)即称为能量平衡方程式。

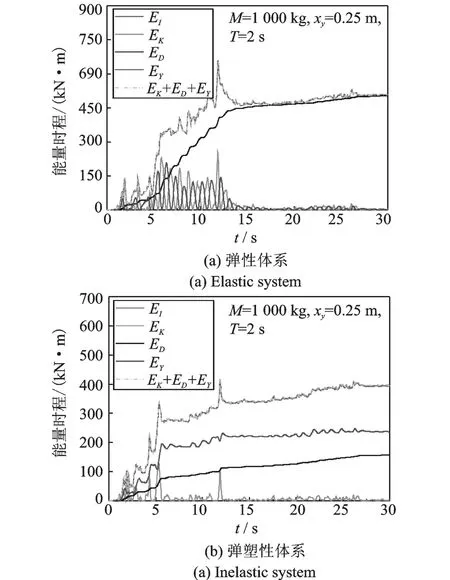
图1 SDOF弹性体系和SDOF弹塑性体系的位移响应时程与能量时程曲线Fig.1 Displacement and energies response of elastic and inelastic SDOF system

图1给出了 El-Centro地震动输入下弹性和弹塑性 SDOF体系的各能量时程曲线。从图 1(a)中可知,对于弹性体系,当地震动趋于结束时,结构的动能EK和弹性变形能ES均趋于 0,由于体系处于弹性,滞回耗能EH为 0,则地震动总输入能EI完全由结构自身的阻尼耗能ED消耗。从图1(b)中可知,对于弹塑性体系,当地震动趋于结束时,地震动总输入能EI主要由结构的滞回耗能EH和阻尼耗能ED共同消耗。因此,滞回耗能被认为是最具工程意义的能量指标,是衡量结构塑性累积损伤的重要参数。

为了消除结构质量影响及分析上的方便,常将滞回耗能量EH做如下形式的转化,即采用单位质量等效速度形式

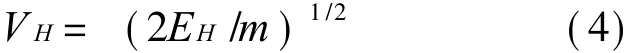
这样,对于不同周期的单自由度体系,便可以计算单位质量等效速度形式的滞回耗能谱,本文在分析过程中采用的是这种滞回耗能量等效速度谱。

2 基于弹塑性位移耦合作用的滞回耗能谱——“VH谱”

2.1 地震损伤模型与“V H谱”表述

Park和 Ang双参数地震损伤模型如下[3,4]

式中xcu为构件在单调加载下的破坏极限位移;Fy为构件的屈服剪力;xm和Eh为构件实际的地震最大变形和累积滞回耗能;U为耗能因子,对于延性差的构件U应该取较大值,反之取较小值。由于累积损伤依赖于U的值,U越小就会导致结构损伤指标D越小,文献 [15～17]建议取其均值约 0.15作为反应典型 RC框架结构在往复荷载作用下的行为。对整体结构来说,可认为D＞ 1.0时结构已经倒塌[3,4]。

式(5)可用延性系数表达如下

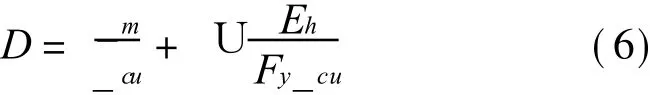
式中xy为屈服位移;_m=xm/xy为最大位移延性系数;_cu=xcu/xy为在单调加载下的破坏极限位移延性系数。

对于具有理想弹塑性恢复力模型的单自由度体系,引入与结构损伤性能指标Di有关的屈服强度折减系数RD,定义如下

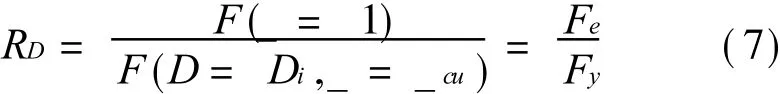
式中F(_=1)表示结构在地震动作用下保持完全弹性所需要的最低强度,即地震作用下的最大弹性剪力Fe;F(D=Di,_=_cu)表示结构在给定的破坏延性系数_cu情况下,结构在相同地震作用下达到给定的损伤状态Di(即进入一定的非线性程度)时所需要的屈服强度Fy。

由RD的表达式(7),可以得到屈服剪力Fy和屈服位移xy,如下:

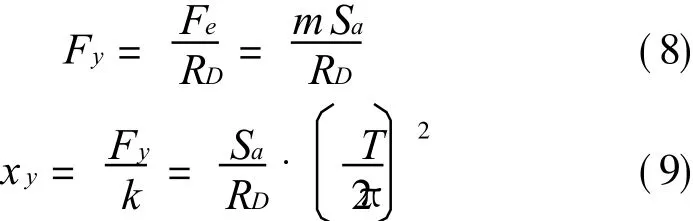
式中Fe为最大弹性剪力,Fy为屈服剪力,Sa为弹性绝对加速度响应的最大值,m为单自由度体系的质量,k为结构初始刚度,T为自振周期。

将式 (8)和(9)代入式(6)即可得到EH-_cu-T-D的表达式

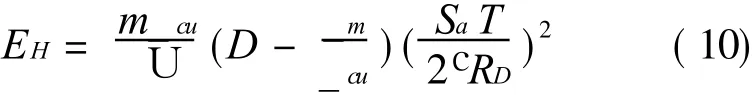
式中 各符号意义同上。对于某一特定的周期T,通过时程分析和程序循环计算可以得到满足各损伤性能Di下的RDi值,进而确定在该RDi值下的滞回耗能EH值,循环周期即可得到相应的谱形式。需要特别指出的是,由于结构考虑极限状态设计,取D=1.0代入式(10),则建立结构在极限状态下的EH-_cu-T的关系,为了消除结构质量影响及分析上的方便,常将式(10)转化为式(4)进行计算,从而得到本文要研究的VH谱。

此外,在具体应用VH谱时,则可以通过建立的VH-_cu-T的关系,由结构的极限破坏延性系数和周期即可方便得到结构的累积滞回耗能,从而进行结构累积滞回耗能评估或设计。

2.2 结构体系的选择

为了通过地震动时程分析得到单自由度体系VH谱,对于结构体系主要考虑了以下几个方面:①周期以 0.1 s时间递增到 6.0 s结束,共计算了 60个单自由度体系;阻尼比a的取值采用工程钢筋混凝土结构常用的0.05。②理想弹塑性恢复力模型应用简便,同时又能较好地模拟结构的非线性性能,且一些研究表明滞回模型对单自由度体系滞回耗能影响不明显的结论[12]。③分别取结构破坏极限位移延性系数_cu为 4,6,8,10和耗能因子U取均值为 0.15进行研究。④取损伤指标D=1,建立极限状态下的VH-_cu-T的关系,以期供抗震性能设计或评估使用。

2.3 地震动的选择和分类

从国外 PEER地震动数据库收集到了大量的水平向记录。由于场地类别对反应谱的影响很大,在对地震记录进行场地分类时,主要参照美国 USGS的分类方法,分为 4类,即基岩类、硬土、一般土和软土,重新分类后所选择的记录数量如表1所示,地震动记录震级与震源距的分布情况见图2。

表 1 USGS场地类别Tab.1 USGSsitegroups

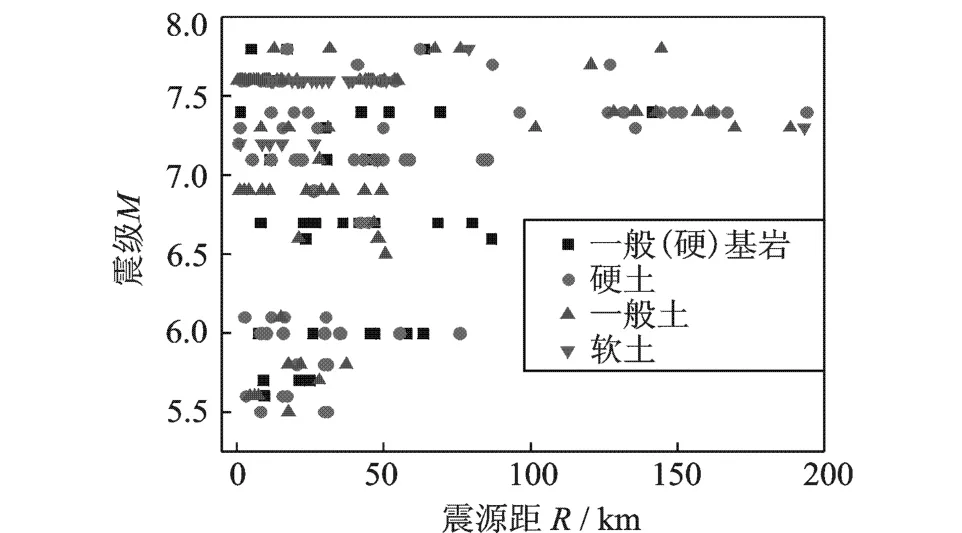
图2 地震动记录震级-震源距的分布Fig.2 Range of magnitudeand hypocentral distance

其次,针对中国现行抗震规范 7度区各类场地在罕遇地震作用下的情况,按现行规范的要求,对所选择的地震动统一调幅为 220 gal。最后,地震动持时采用大多数研究使用的能量有效持时作为加速度的时程,即相应于 5%和 95%Arias强度的时间[18]。

2.4 DBHS程序求解原理及步骤

图3给出了本程序求解过程,具体步骤如下:

(1)首先给定初始结构参数:阻尼比a、极限破坏延性系数_cu和结构耗能因子U;

(2)选择初始周期T1;

(3)输入地震动记录,并计算最大弹性剪力Fe;

(4)通过折减系数RD,由式(8)和 (9)求解屈服剪力Fy和屈服位移xy;

(5)通过运动方程求解结构的响应,即求出最大位移延性系数_m和塑性耗能项Eh;

(6)将Eh和_m代入式(10),求出D值;

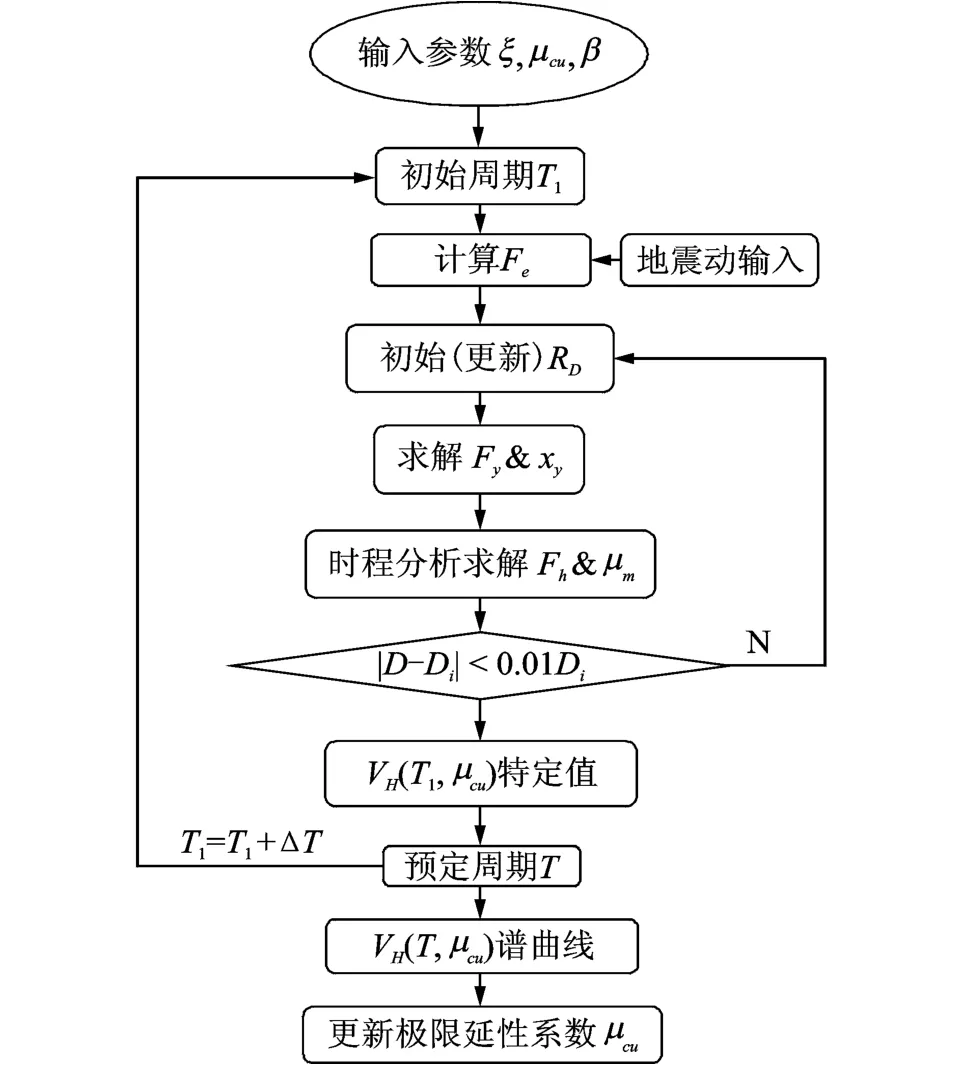
图3 VH求解程序Fig.3 Procedure for constructing V H spectra

(7)更新修改折减系数RD,重新得到Fy和xy,重复步骤(3)到(6)直到D满足规定的损伤指标值Di,例如,0.3,0.5和0.7等等;本文研究考虑结构采用极限状态设计,取Di=1.0。

(8)求出特定周期T1且满足Di=1.0的滞回耗能谱VH(T1,_cu)值;

(9)增加周期,T1=T1+ΔT返回到第(2)步;

(10)重复以上步骤直到周期达到预定T值,即可得到VH(T,_cu)谱 ,即“VH谱”。

(11)改变破坏延性系数_cu,重复步骤(2)～(10),即可建立一系列VH谱曲线。

2.5 VH谱及其基本特征

通过以上程序及分析,计算了 4类场地类别对应阻尼比为5%且具有理想弹塑性特性的单自由度体系的均值VH谱,见图4。从这些图中可以得出其如下一些基本特征:

(1)对于指定的周期来讲,滞回耗能量(即VH谱值)随破坏延性系数的增加而增大,但并不是延性系数越大,滞回耗能量越大,当破坏极限延性系数大于6之后,滞回耗能量差别不是很大,甚至在中长周期段(T＞3.0 s),滞回耗能量反而出现随破坏极限延性系数的增大而变小的情况,也就是说,增大结构延性系数,可以增加结构在地震中的滞回耗能量,但并不是延性系数越大越好。这个特征与文献[12]研究得到的结论是基本一致的。

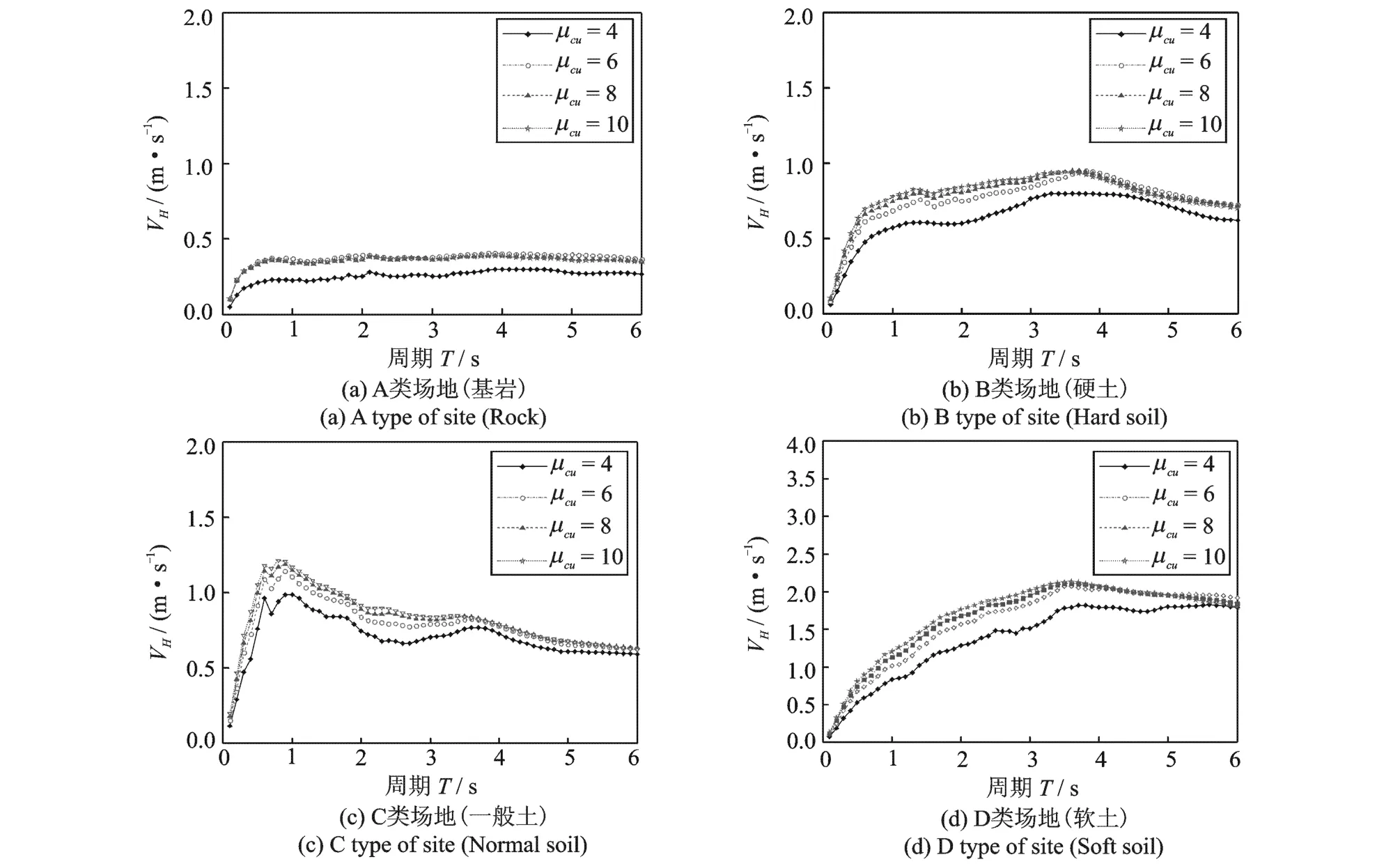
图4 各类场地的均值V H谱Fig.4 Mean VH spectra of four sitegroups

(2)对于特定的破坏延性系数,滞回耗能量随周期的变化而变化,尤其在短周期范围内,周期变化对滞回耗能量影响较大,随周期的增加上升较快;但在长周期范围内,周期对滞回耗能量影响相对较小,滞回耗能量逐渐趋于稳定的值。

(3)场地条件对滞回能量的影响很大,随着场地的变软,滞回耗能量变大,因此在利用滞回耗能量做性能设计或评估时,场地条件应当给予充分的考虑。

2.6 VH谱的拟合公式

根据VH谱以上分析的规律和特征,结合所选定的拟合模型,下面将分别拟合出4类场地上VH谱的近似计算公式,以便应用于结构抗震设计或评估使用。文中没有讨论震中距、地震波传播路径等地震动特性对VH谱的影响。但屈服强度系数、系统的自振周期和场地条件往往是影响反应谱的重要因素,因此在回归分析中主要考虑了这3个因素的影响。

由图4可以看出,各类场地的VH谱曲线具有比较一致的变化趋势和形状,因此,可采用统一的函数式表示如下

通过构造如下的函数形式来拟合得到各类场地的VH谱

其中拟合参数A和B可用以下三次多项式表达

式中a1,a2,a3,a4,b1,b2,b3和b4分别为回归系数。

通过两步回归可得到各类场地VH谱的各回归系数,见表2。图 5为VH谱的拟合曲线与统计曲线的比较,由图可知,除 C类场地(一般土)在短周期范围内(T＜2 s)的拟合效果不佳外,在具体应用时可进行适当的修正,其他各类场地拟合效果均可满足工程精度要求,具体应用时可直接使用。

表2 拟合公式中的有关参数Tab.2 Parameters of regressive formulas

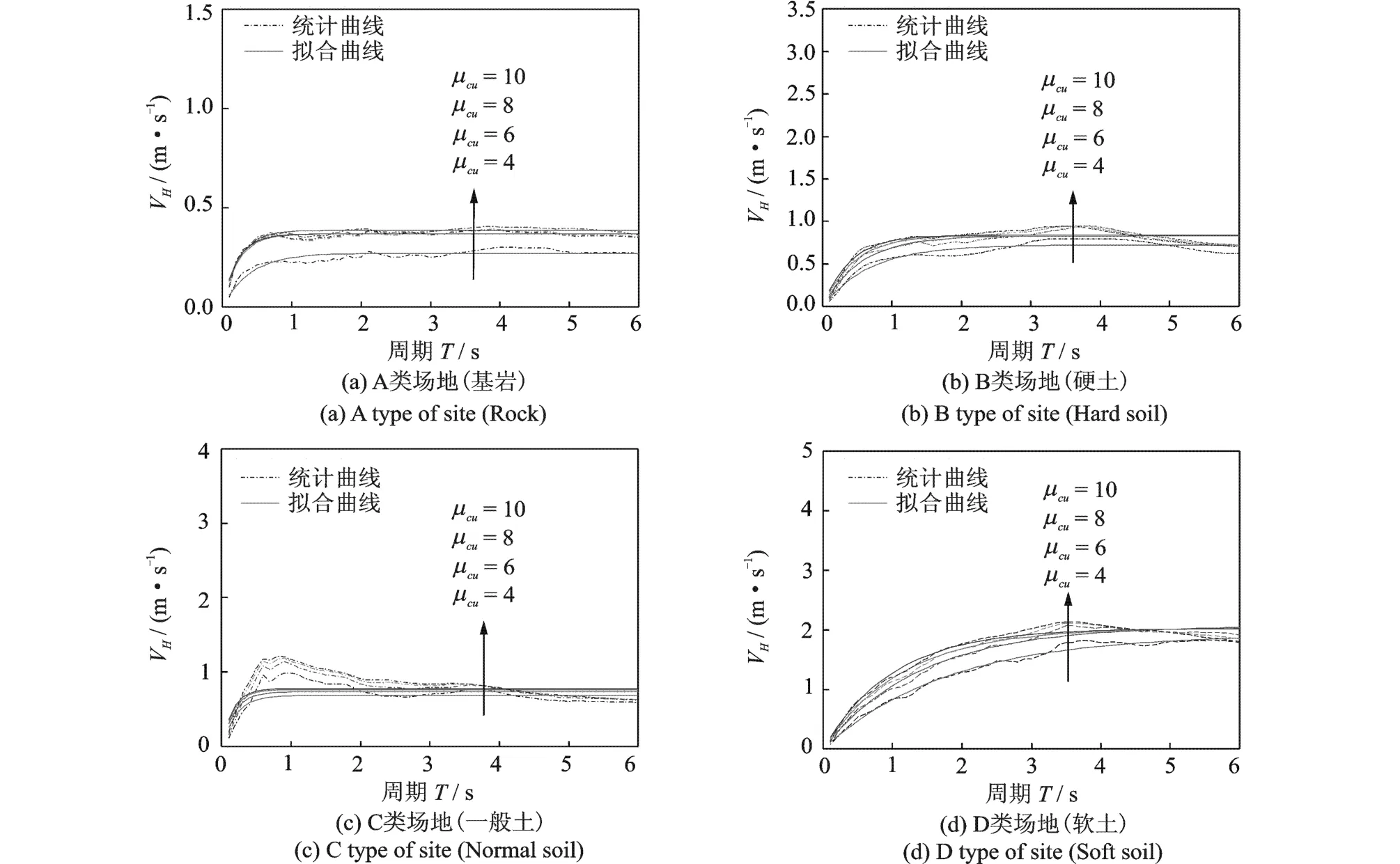
图5 均值VH谱的拟合曲线与统计曲线Fig.5 Mean curves and regressed curves of V H spectra

3 结 论

本文研究了抗震结构基于最大位移耦合作用的滞回耗能谱,得到如下结论:

(1)抗震结构的损伤应当综合考虑最大位移响应和累积损伤的耦合作用,研究得到的VH谱则综合考虑了二者因素,有别于以往研究的仅考虑能量因素的滞回耗能谱,能够更加合理地反映结构在罕遇地震作用下的弹塑性行为,利用本文的研究结果进行滞回耗能量评估相对于其他滞回耗能谱则更加准确。

(2)对于指定的周期来讲,增大结构延性系数,可以增加结构在地震中的滞回耗能量,但并不是延性系数越大越好,当破坏极限延性系数大于 6之后,滞回耗能量差别不是很大,甚至在中长周期段(T＞3.0 s),滞回耗能量反而出现随破坏极限延性系数的增大而变小的情况;对于特定的破坏延性系数,在短周期范围内,周期变化对谱值的影响较大,随周期的增加上升较快,但在长周期范围内,周期对谱值影响较小,谱值逐渐趋于相对稳定的值;此外,场地条件对滞回能量的影响很大,随着场地的变软,滞回耗能量变大,因此在利用滞回耗能量做性能评估或设计时,场地条件应当给予充分的考虑。

(3)通过对大量的 SDOF体系的弹塑性时程分析计算和拟合回归分析,建立了各场地类别VH谱的计算公式,并回归了相应的系数,研究成果可供抗震性能设计或评估应用。需要指出的是,本文得到的VH谱考虑的是极限状态情况,即Di=1.0,根据本文方法,可以得到其他损伤指标值下的类似情况。

[1] Housner G W.Limit design of structures to resist earthquakes[A]. Proc.of First World Conf.on Earthquake Engineering[C].Berkerly,CA,1956,5:1—11.

[2] Luis D.Decanini,Fabrizio Mollaioli. An energybased methodology for the assessment of seismic demand[J].Soil Dynamics and Earthquake Engineering,2001,21(2):113—137.

[3] Park Y J,Ang A H-S.Mechanistic seismic damage model for reinforced concrete[J].Journal of Structural Engineering ASCE.,1985,111(4):722—739.

[4] Park Y J,Ang A H-S.Seismic damage analysis of reinforced concrete buildings[J].Journal of Structural Engineering ASCE.,1985,111(4):740—756.

[5] Phaiboon Panyakapo. Evaluation of site-dependent constant-damagedesign spectrafor reinforced concrete structures[J].Earthquake Engineering and Structural Dynamics,2004,33:1 211—1 231.

[6] Kunnath S K,Chai Y H.Cumulative damage-based inelastic cyclic demand spectrum[J].Earthquake Engineering and Structural Dynamics,2004,33:499—520.

[7] Yong Lu,Jianwu Wei.Damage-based inelastic response spectra for seismic design incorporating performance considerations[J].Soil Dynamics and Earthquake Engineering,2008,28(7):536—549.

[8] 肖明葵,刘刚,白绍良,等.抗震结构的滞回耗能谱[J].世界地震工程,2002,18(3):110— 115.Xiao Mingkui,Liu Gang,Bai Shaoliang,et al.The hysteretic energy spectra of seismic structures[J].World Earthquake Engineering,2002,18(3):110—115.

[9] 公茂盛,翟长海,谢礼力 ,等.地震动滞回能量谱衰减规律研究 [J].地震工程与工程振动,2004,24(2):8—14.Gong Maosheng,Zhai Changhai,Xie Lili,et al.Study on attenuation of hysteretic energy spectra of strong ground motion[J].Earthquake Engineering and Engineering Vibration,2004,24(2):8—14.

[10]程光煜,叶列平.弹性多自由度系统地震输入能量的研究 [J].工程抗震与加固改造 ,2006,28(4):6— 9.Cheng Guangyu,Ye Lieping.Research on seismic energy demand of elastic MDOF system[J].Earthquake Resistant Engineering and Retrofitting,2006,28(4):6—9.

[11]杨晓明,史庆轩,丰定国.抗震结构能量设计方法中阻尼耗能的研究[J].西安建筑科技大学学报(自然科学版),2006,28(2):189—198.Yang Xiaoming,Shi Qingxuan,Feng Dingguo.Study on dissipative energy in energy method of seismic structures[J].J.of Xi′an Univ.of Arch.& Tech.(Natural Science Edition),2006,28(2):189—198.

[12]翟长海,谢礼力,吴知丰.基于台湾集集地震的结构滞回耗能影响分析[J].哈尔滨工业大学学报,2006,38(1):59—62.Zhai Changhai,Xie Lili,Wu Zhifeng.Influence analysis on hysteretic-energy based on 1999 Chi-Chi,taiwan earthquake[J].Journal of Harbin Institute of Technology,2006,38(1):59—62.

[13]盛明强,罗奇峰.Northridge与ChiChi地震滞回耗能谱的比较 [J].同济大学学报(自然科学版),2008,36(10):1 315—1 319.Sheng Mingqiang,Luo Qifeng.Comparison of hysteretic energy spectra in northridge and ChiChi earthquake[J].Journal of Tongji University(Natural Science),2008,36(10):1 315—1 319.

[14]滕军,董志君,容柏生,等.弹性单自由度弹性能量反应谱研究 [J].建筑结构学报,2009,30(S1):129—133.Teng Jun,Dong Zhijun,Rong Baisheng,et al.Energy spectra of elastic SDOF systems[J].Journal of Building Structures,2009,30(S1):129—133.

[15]Cosenza E,Manfredi G.A seismic design method including damage effect[A].In:11 th European Conference on Earthquake Engineering[C].Paris,1998:1—11.

[16]Chai Y H,Romstad K M,Bird S M.Energy-based linear damagemodel for high-intensity seismic loading[J]. Journal of Structural Engineering(ASCE),1995,121(5):857—864.

[17]Park Y J,Ang A H-S,Wen Y K.Damage-limiting a seismic design of buildings[J].Earthquake Spectra,1987,3(1):1—26.

[18]Bommer J J,Martinez-Pereira A.The effective duration of earthquake strong motion[J].J.of Earthquake Engineering,2006,26(1):1—13.