基于并联机构的六维加速度传感器的方案设计及建模研究✳

尤晶晶,李成刚,吴洪涛

(1.南京航空航天大学机电学院,江苏南京 210016;2.江苏省精密与微细制造技术重点实验室,江苏南京 210016)

引 言

惯性导航系统是一种不依赖于外部信息、也不向外部辐射能量的自主式导航系统,通过测量运载体在惯性参考系中的加速度,再经过积分可以解算出载体的速度、偏航角、位置等导航参数。目前,惯性导航系统中惯性测量装置一般包括 3个单轴加速度计和3个陀螺仪,分别测量运载器在三维空间内3个线加速度以及 3个角速率。加速度计与陀螺仪是分离的元件,不但体积大、成本高、缺乏角加速度信息,而且对于控制大姿态角、大机动状态的运动都很困难[1,2]。应用一体化的六维加速度传感器直接获取上述信息,不但可提高精度和带宽,而且可节省空间和成本,对提升导航系统的控制性能,尤其是高机动导弹、无人机等新型飞行器具有重要意义[3,4]。另外,六维加速度传感器在机器人、车辆、生物医疗等领域的振动测量方面都有着非常广泛的应用前景[5～7]。

目前,单轴加速度传感器的技术比较成熟,基于压电、压阻、光纤等检测机理的各种传感器,市场上都有相应的产品[8]。多维加速度传感器在市场上并不多见,国内外科学家对其研究也主要集中在三维领域[9]。至于可以同时测量载体加速度6个分量的传感器还未进入市场,国内外的研究都不多,尚处于探索阶段。 FENG J采用静电悬浮原理设计了六维加速度传感器[10],通过测量电容的变化来计算加速度,具有测量精度高的优点,适合于测量微重力或低温环境下量程较小的加速度。重庆大学设计的一种组合式六维加速度传感器是将六只单轴压电加速度计首尾相连[11],以垂直正交的立方体布局结构固定在各安装平面上,利用该结构可以实现运动载体六维加速度的传感,并具有结构紧凑的优点。从检索到的文献来看,六维加速度传感器普遍存在完全解耦困难、结构复杂、加工及安装要求高等缺陷。进行六维加速度传感器的设计已经成为传感器研究领域的一项重要课题,有着巨大的理论意义和实际价值[12]。

本文提出一种新的基于并联机构的压电式六维加速度传感器的设计方案,在阐明工作原理的基础上,详细推导了待测六维加速度的解耦过程。最后,通过将由数学模型计算的结果与ADAMS仿真结果进行对比以及将实物样机的试验结果与激振器的标准输出值进行对比,有效验证了设计方案的合理性和可行性。鉴于六维加速度传感器的灵敏度等性能目前还没有统一、规范的定义,且缺乏综合性能评价指标,本文不在性能方面与其他方案进行对比。

1 工作原理

考虑到并联机构具有刚度大、精度高、承载能力强、动力学性能好、结构紧凑且稳定等优点[13],对其进行理论和应用方面的研究已逐渐成为学术界的热点,另外,压电陶瓷具有重量轻、灵敏度高、压电系数大、信噪比大、频响特性好、性能稳定可靠等优点[14],且特别适合于加速度的测量[15],本文提出一种将并联机构作为六维加速度传感器的弹性体结构,并用压电陶瓷充当传感器敏感元件的设计方案,其三维模型如图1所示。涉及到的并联机构具有9条相同的 SPS支链,其中,S代表球面副,这里设计成弹性球铰链,具有体积小、无间隙、无摩擦等优点;P代表移动副,圆柱状压电陶瓷在轴向力作用下沿其极化方向会产生一定量的弹性变形,故可视为移动副。每3条SPS支链为一组,它们一端的弹性球铰链固结在一起,组合成复合弹性球铰链并固结于立方体质量块一面的几何中心;另一端的弹性球铰链分别固结于外壳上相邻的相互垂直的3个面。

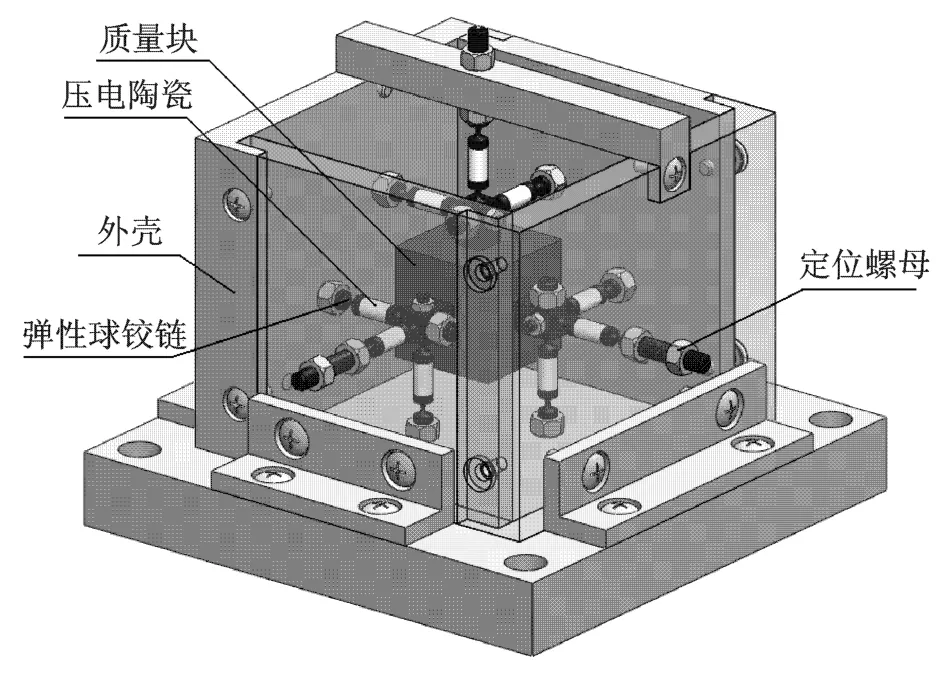
图1 六维加速度传感器三维模型Fig.1 Three-dimensional model of six-axis accelerometer

传感器的加工及装配容许存在一定的误差,除了定位螺母可对各支链进行调节外,还可通过建立误差模型和进行标定试验进一步补偿。鉴于与复合弹性球铰链相联结的3条支链转动中心保持重合会给加工带来极大困难,将转动中心设计成沿各轴线方向延长线重合可以大大降低加工难度,实际计算时只需将支链长度进行相应修改即可。

传感器工作时,其外壳底板刚性固定在待测体上,保证传感器外壳运动的加速度即为待测的六维加速度。在惯性力和惯性力矩作用下,质量块压缩或拉伸9组压电陶瓷。压电陶瓷重量轻,且两端连接球面副,故每条SPS支链可视为二力杆。由于正压电效应,压电陶瓷在沿极化方向作用力下其极化面上会产生电荷。9组压电陶瓷两极通过单面导电膜以及环氧树脂胶与铰链固结,并从铰链的凹槽引出导线,导线分别连接电荷放大器 9个通道的输入端,放大器输出端输出经过信号放大和阻抗变换处理之后的电压模拟量,再通过数据采集卡将其转换成数字量供计算机分析处理。

2 数学模型

2.1 运动学模型

为便于建立系统的运动学、动力学模型,将图 1的三维模型进行简化。用直线表示压电陶瓷,空心圆圈表示弹性球铰链,实心圆圈表示复合弹性球铰链,简化后的模型如图 2所示。

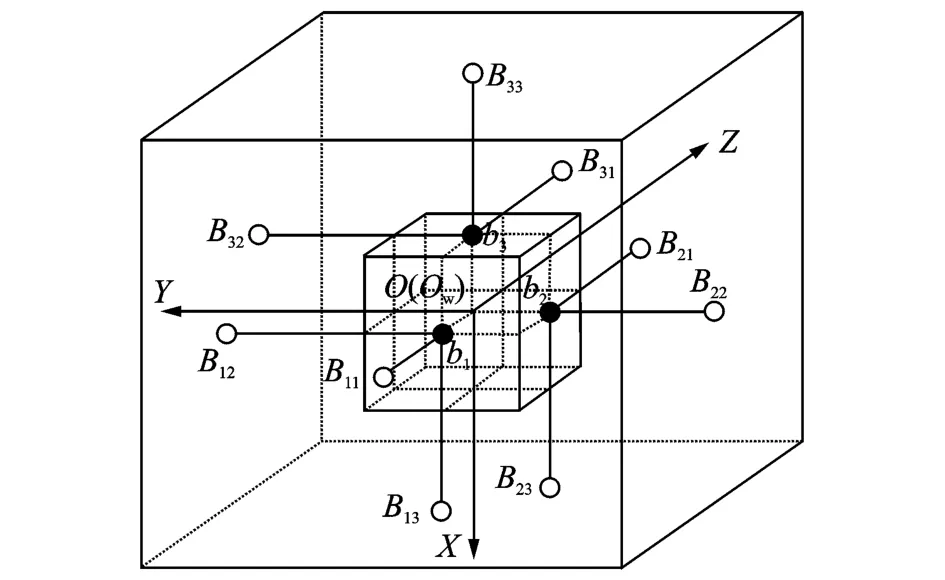
图2 六维加速度传感器简化模型Fig.2 Simplified model of six-axis accelerometer

在质量块上固结坐标系{M},其坐标原点选为质量块的质心,3条坐标轴分别平行于质量块的3条棱边。在外壳上固结坐标系{W},与初始状态时的{M}重合,并将其坐标原点记为OW。图 2中b1,b2,b3分别表示固结在质量块前表面、右表面和上表面几何中心处的复合弹性球铰链;B11～B33表示固结在外壳上的弹性球铰链。各条 SPS支链的初始长度设为L,质量块的边长设为 2n,则坐标系{W}原点与固结在外壳上各弹性球铰链的中心连线的矢量可以分别表示为

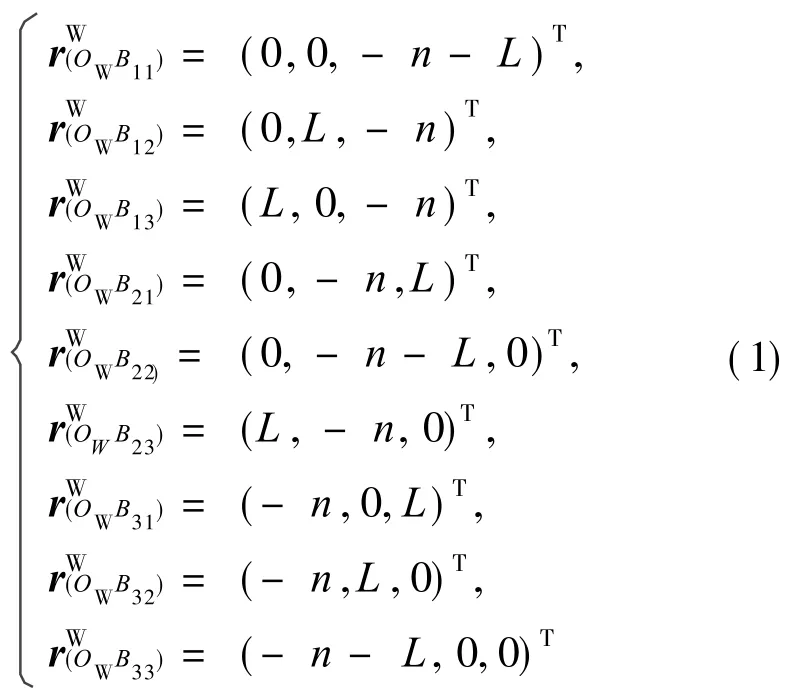
式中 上标“W”表示矢量投影在坐标系{W}中,下标括号中的第1个点为矢量起点,第2个点为矢量终点。

为便于建模,将坐标系{W}原点与 3个复合弹性球铰链的中心连线的矢量分别表示为

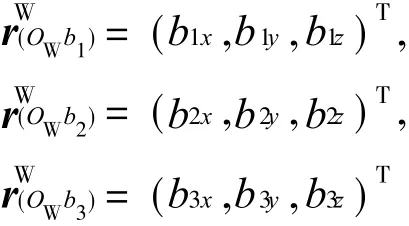
圆柱状压电陶瓷刚度K的计算表达式

式中L0,D,S33分别表示压电陶瓷的原长、底面圆直径和弹性柔顺系数。

根据数据采集卡第i通道输出的电压值Ui,计算第i个压电陶瓷上受到的轴向力大小

式中Sq,Su分别为在电荷放大器控制面板上设置的输入电荷灵敏度和输出电压灵敏度;d33为压电陶瓷的压电系数。

传感器工作过程中,第i条 SPS支链的长度为

另外,每条 SPS支链的长度还可以通过两端弹性球铰链的几何坐标来计算,以第一组 SPS支链为例列写计算表达式

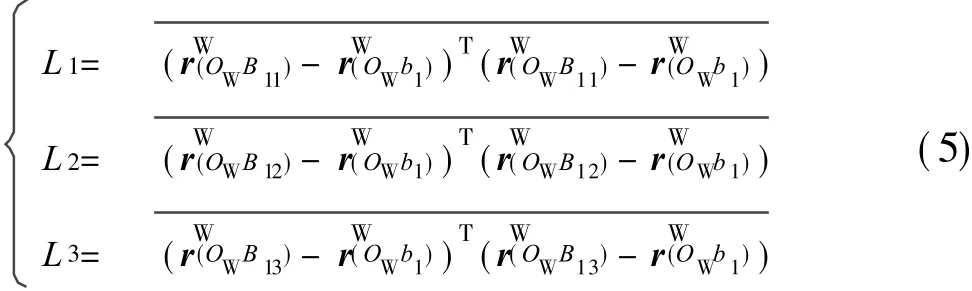
将式(1)代入(5)求解方程组,计算得到两组解。考虑到传感器实际工作时,复合弹性球铰链b1不会运动至图 2所示的平面B11B12B13的另一侧,故仅有一组解满足传感器的结构要求,即

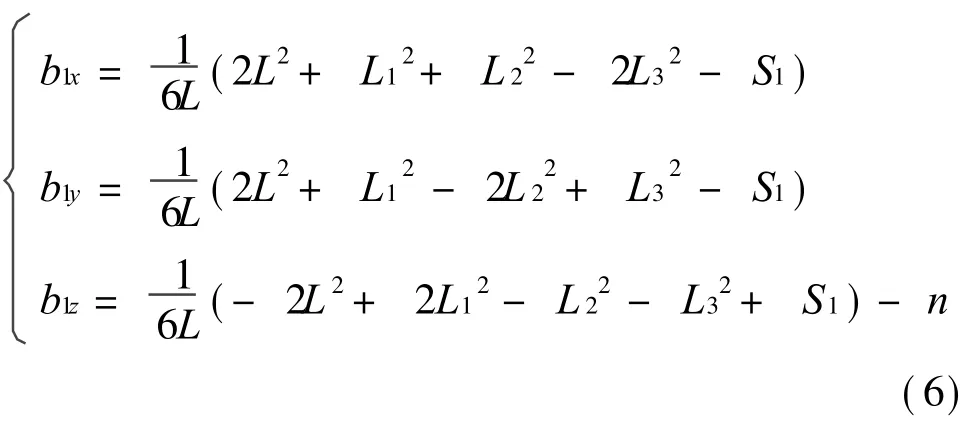
其中,S1=L12L32+L22L32,S12=L12+L22+L32,S13= 4L4+

同理,可以列出其他两个复合弹性球铰链几何坐标的解析表达式。

如图 3所示,将{M}的坐标原点记为O′;b1,b2,b3组成边长为的正三角形。将O′在面b1b2b3上的投影记为O″,过O″分别作直线O″p1,O″p2平行于b1b3和b2b3,p1和p2为交点。

图3 质量块位姿计算模型Fig.3 Calculation model of position and pose of the mass-block

运用立体几何知识,连接坐标系{W}和{M}的坐标原点所形成的矢量可以表示为

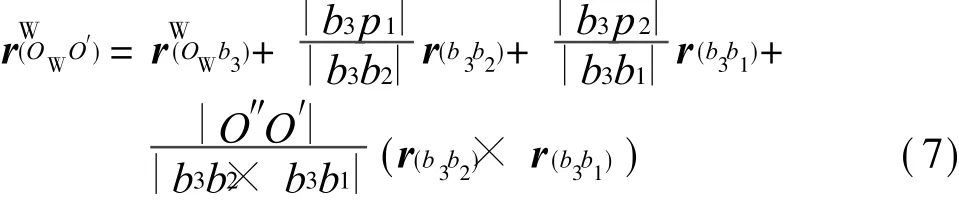
其中,|b3p1|=|b3p2|=r(b3b2)= (b2x-b3x,b2y-b3y,b2z-b3z)T;r(b3b1)= (b1xb3x,b1y-b3y,b1z-b3z)T。

另外,{M}相对于{W}的旋转矩阵在 {W}中投影为

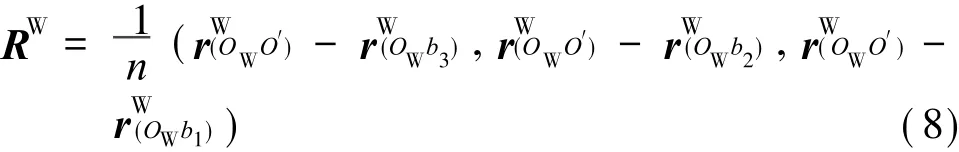
式(7),(8)即为该并联机构的位置正解,显然,等号右边各项可以用关于系统结构参数和支链实时长度的解析式来表示。

将 3个复合弹性球铰链的速度矢量分别记为:

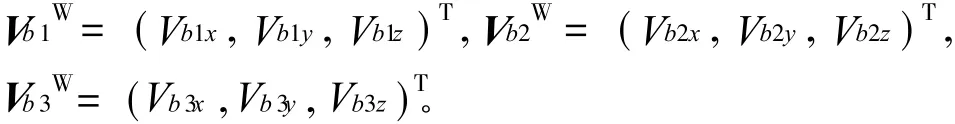
式(6)对时间求一阶导数,得到b1速度矢量中各分量的解析表达式

同理,可列出其他 2个复合弹性球铰链速度的表达式。将{M}的坐标原点在{W}中运动的线速度矢量以及{M}相对于{W}转动的角速度矢量分别记为和kW,它们与复合弹性球铰链的速度矢量之间满足关系:

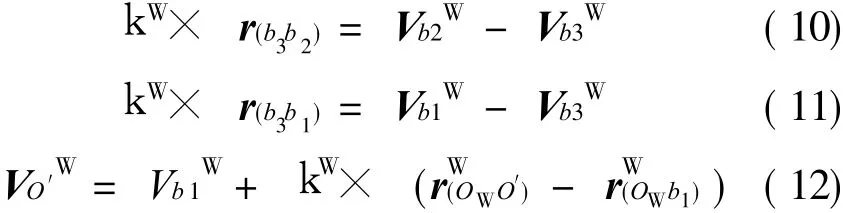
由式(10),(11),易得到kW关于复合弹性球铰链坐标以及速度的解析表达式,再将其代入式(12)即得到的解析表达式,限于篇幅这里不具体列出。

将 3个复合弹性球铰链的加速度矢量分别记

式(9)对时间求一阶导数,得到b1加速度分量的表达式

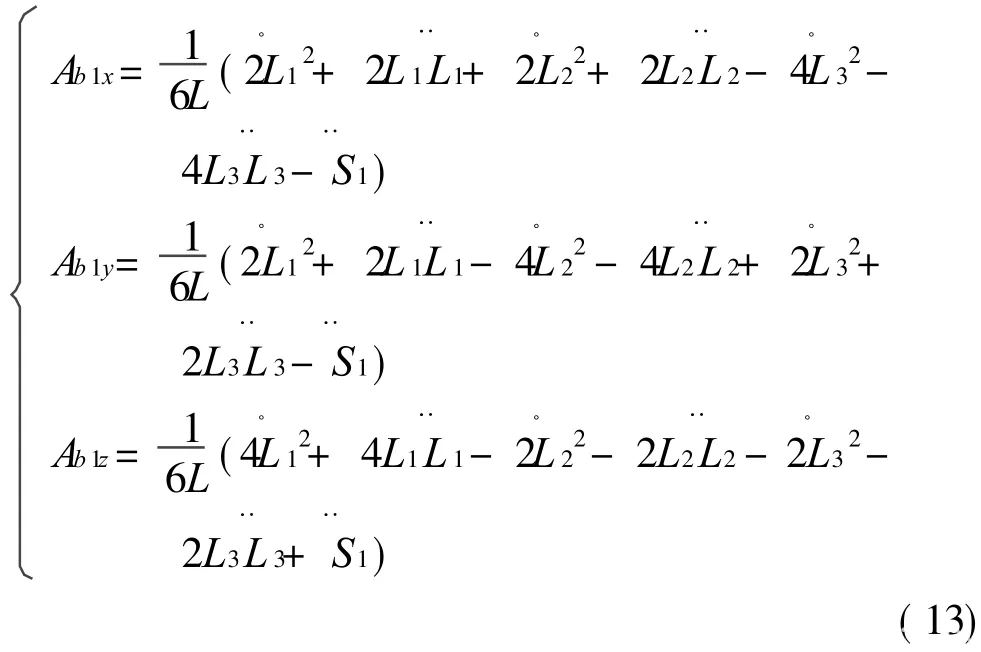
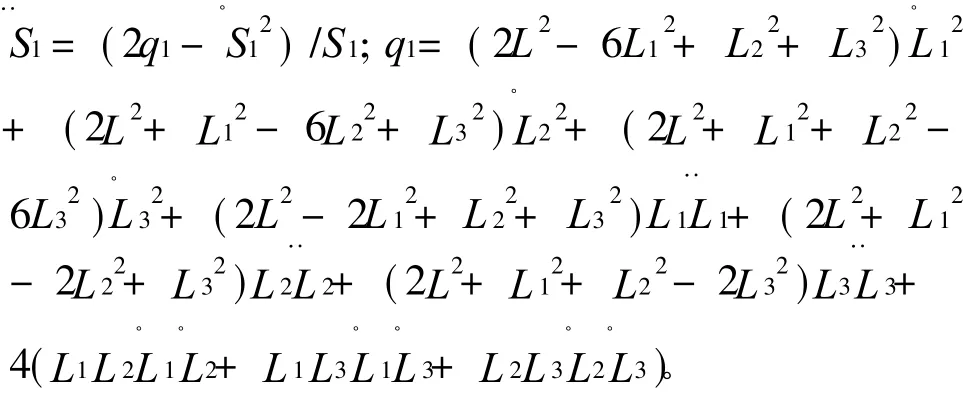
同理,可以列出其他 2个复合弹性球铰链加速度的解析表达式。点O′在{W}中运动的线加速度矢量以及{M}相对于{W}转动的角加速度矢量分别记为和XW,它们与复合弹性球铰链的速度、加速度之间满足关系:

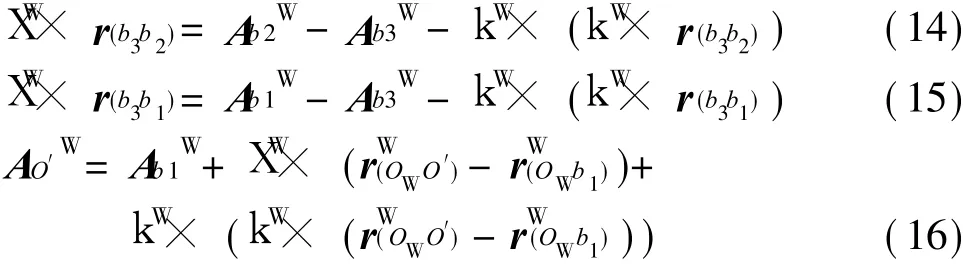
由式(14),(15),易得到XW关于复合弹性球铰链坐标、速度以及加速度的解析表达式,再将其代入式(16)即得到 AO′W的表达式。

在地面上固结惯性坐标系{O}并使其与初始状态时的{M}重合。将{W}相对于{O}转动的角速度矢量记作kO,上标“O”表示该矢量是在{O}中投影的。根据角速度加法公式,计算{M}相对于{O}转动的角速度矢量,也即质量块的绝对角速度

式(17)对时间求一阶导数,并运用变矢量的绝对导数与相对导数定理[16],得到质量块的绝对角加速度

将连接{O}与{W}坐标原点的矢量记为rO(OOW),则{M}的坐标原点在{O}中运动的线速度,也即质量块质心的绝对线速度可以表示为

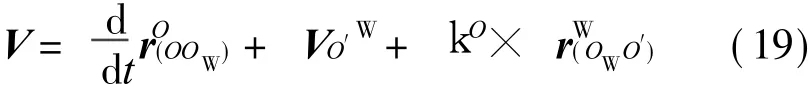
式(19)对时间求一阶导数,得到质量块质心绝对线加速度的表达式

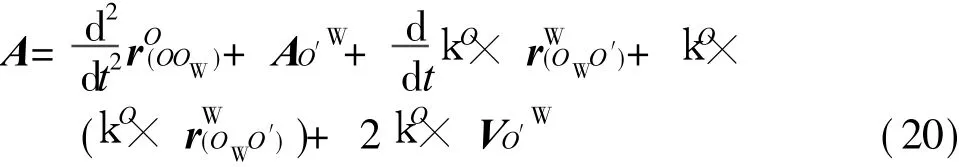
2.2 动力学模型

作用在质量块上的外力包括沿 9条 SPS支链轴线方向的压缩(拉伸)力以及质量块自身的重力,其合力以及对质心的合力矩分别为:

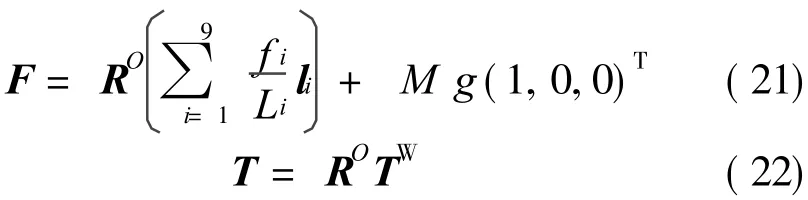
式中 RO为{W}相对于{O}的旋转矩阵;M为质量块的质量;g为重力加速度;

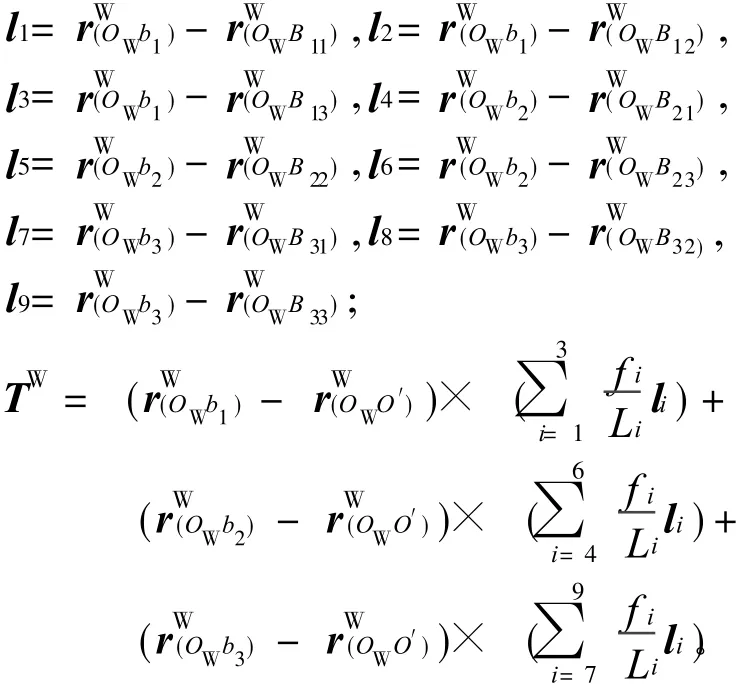
根据牛顿-欧拉法,建立传感器系统的动力学方程,也即系统的振动微分方程组:

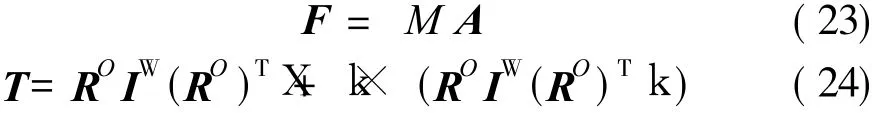
式中 IW表示在坐标系{W}中描述的质量块的惯性张量,且满足关系IW=RWdiag(2Mn2/3,2Mn2/3,2Mn2/3)(RW)T。

综合式(17),(18),(22),(24),并将所有的矢量投影在坐标系{O}中,得到如下形式的高度耦合的微分方程

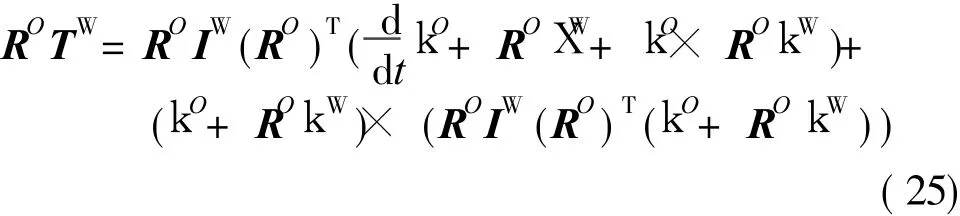
引入辅助角速度k*,使其满足下面关系式

式(26)等号两边对时间求一阶导数

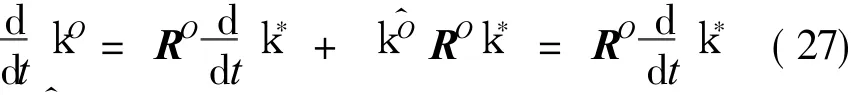
将式(26),(27)代入 (25),并考虑到 RO为正交矩阵,化简整理后得到不含RO的微分方程

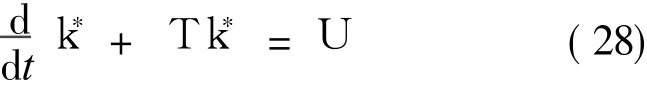
假设传感器外壳由静止开始运动,可以通过求解式(29)所示的一阶常微分方程组的初值问题来计算k*。

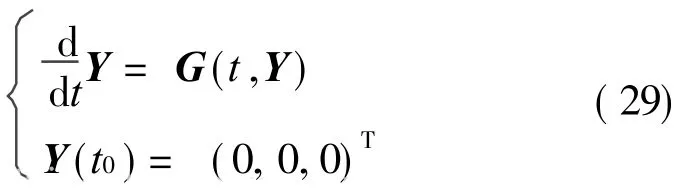
式中 Y=k*;G(t,Y)=U-Tk*。

易证明函数G(t,Y)关于Y满足 Lipschitz条件,运用改进的欧拉算法求解方程组(29),其递推公式为

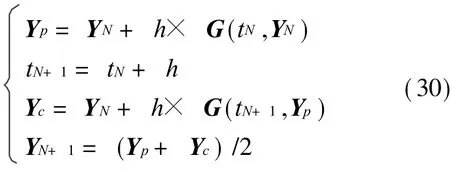
式中h为计算步长;下标N,p,c分别表示第N步数值、预测值和校正值。

坐标系旋转矩阵的描述方法通常有方向余弦、欧拉角等,为便于实现六维加速度的实时解耦,使用四元数来描述正交矩阵RO,即

其中,

λ1,λ2,λ3,λ0为单位四元数Λ的各分量 ,且满足:Λ=(λ1,λ2,λ3,λ0)T。

另外,刚体的角速度矢量也可以用描述旋转矩阵的四元数及其对时间的一阶导数来表示

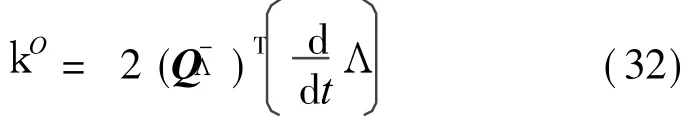
综合式(26),(31),(32),化简后得到关于四元数Λ的微分方程组

显然,传感器外壳处于初始位姿时,其旋转矩阵为单位阵,即

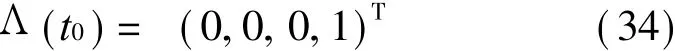
同样运用改进的欧拉算法求解式(33),(34)组成的一阶常微分方程组的初值问题。

需要指出的是,单位四元数的各分量之间还必须满足约束方程(35),由于计算过程中存在截断误差和舍入误差,四元数不再满足该约束方程,也即存在违约问题。

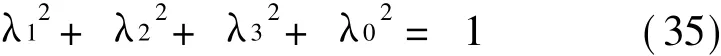
将通过微分方程组数值计算得到的四元数、四元数的理论值以及计算误差分别记为λ~i,λi和Δλi。

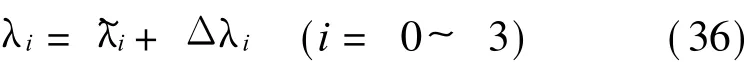
综合式(35),(36),并运用泰勒公式在数值计算值处展开,忽略二阶以上无穷小量,得到

由式(37)并根据矩阵广义逆理论,计算姿态四元数在每一个节点处的修正值

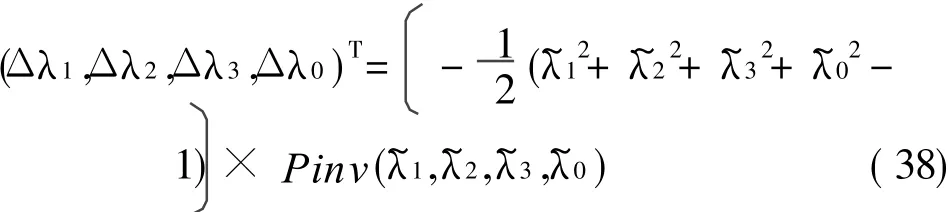
式中Pinv(· )表示矩阵的广义逆。

将经过违约修正之后的单位四元数Λ代入式(31),(26),(27),分别计算RO,kO和d kO/dt;再结合式 (20),(21),(23),计算 d2r(OOW)O/dt2。 其中,d2r(OOW)O/dt2和d kO/dt分别表示传感器外壳运动的线加速度矢量和角加速度矢量,也即待测的六维加速度。

3 算例验证

3.1 仿真验证

ADAMS是目前国际上应用最为广泛的虚拟样机分析软件,具有强大的运动学、动力学分析功能和先进的求解算法。为验证数学模型的可靠性,在ADAMS/View模块中建立六维加速度传感器的虚拟样机,如图 4所示。

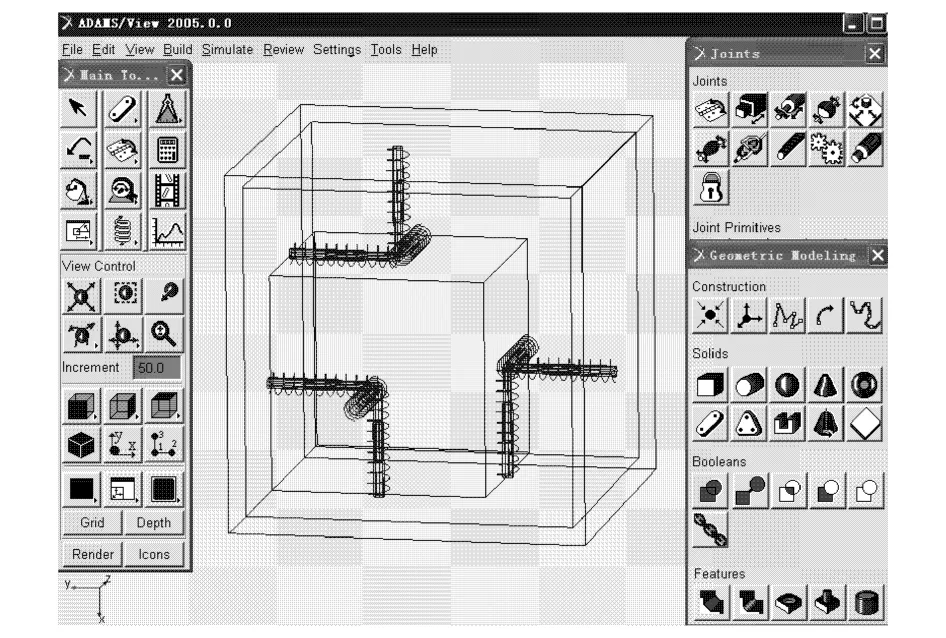
图4 六维加速度传感器虚拟样机Fig.4 Virtual prototype of six-axis accelerometer

在传感器外壳上同时施加直线驱动和旋转驱动,其方向矢量分别为(5,-6,7)和(17,12,-20),线位移函数和角位移函数分别为:Γ=19.859×cos(10π×t)- 19.859(mm)和 Θ= 0.524×cos(10π×t)-0.524(rad)。设定仿真步长为0.002 s,仿真时间为2 s,对虚拟样机进行动力学仿真。测量9条支链的伸长量,在 Post-Processor模块中将其数据导出并导入根据数学模型编写的 M ATLAB程序中,数据输入、计算、显示和保存的时间之和仅为1.64 s。将解算得到的六维加速度与在 ADAMS中仿真时外壳运动的六维加速度进行数据对比,结果如图 5(a)～ (f)所示,显示两者吻合得很好。 误差主要来源于数值微分和微分方程数值求解过程中的截断误差和舍入误差,以及 ADAMS软件中测量数据初始点的摄动和中间点的扰动。由式(20)可知,待测线加速度的计算误差中除了包含角加速度的计算误差外,还包含了角速度的计算误差以及并联机构运动学的计算误差,这与图 5反映出的线加速度和角加速度的误差大小关系是完全吻合的。

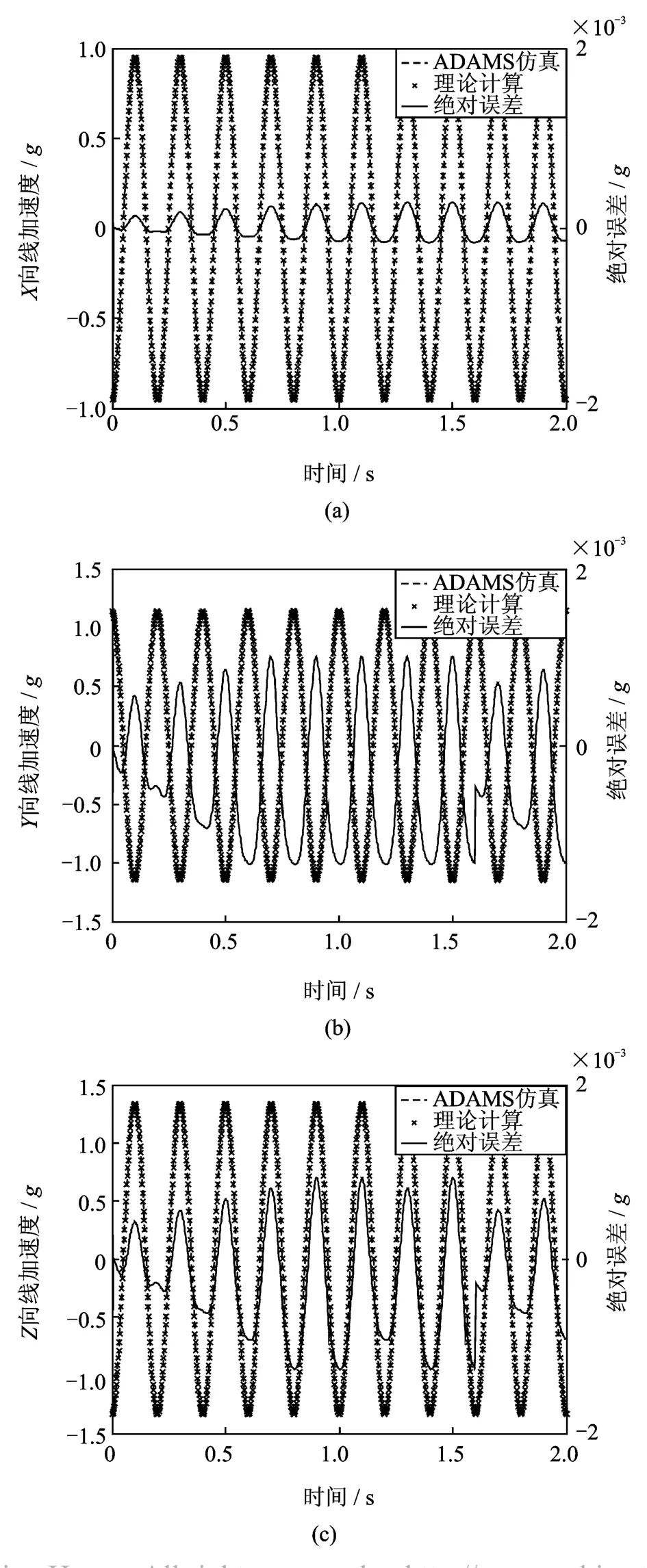
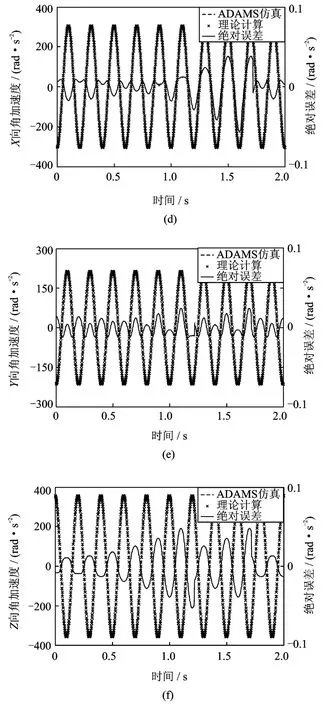
图5 理论计算与 ADAMS仿真对比Fig.5 Comparison between theoretical calculation and simulation with ADAMS

3.2 试验验证

为进一步验证本文设计方案的可行性,加工制作了六维加速度传感器的实物样机,并将其安装在激振器上进行了振动测试实验,如图6所示。利用第2节中建立的数学模型及其算法对9组压电陶瓷输出的经过剔除、滤波、放大等调理后的电压信号进行数据处理,其中在求解微分-代数方程组(33)和(35)时分别运用传统增广法和违约修正法进行处理。将解算到的两组六维加速度与激振器输出的标准加速度进行对比,一方面显示了试验结果与标准输出值吻合得较好;另一方面显示了 2.2节中违约修正算法的有效性,限于篇幅,这里仅给出X方向线加速度的对比曲线,如图 7所示。其中,违约修正法的误差主要来源于传感器的加工、安装误差以及压电陶瓷电压信号的输出误差和调理误差,可通过进一步的标定研究来提高六维加速度传感器的测量精度。

图6 六维加速度传感器实物样机及试验平台Fig.6 Physical prototypes and experimental platform of six-axis accelerometer

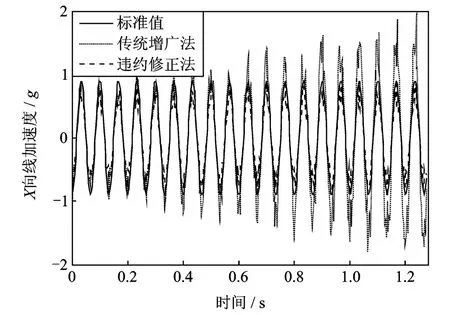
图7 实物样机试验验证Fig.7 Experimental verification of physical prototypes

4 结 论

(1)提出了一种基于并联机构的压电式六维加速度传感器的设计方案。用一种特殊构型的具有 9条 SPS支链的并联机构充当传感器的弹性体结构,压电陶瓷同时充当传感器的敏感元件和并联机构的移动副,用弹性球铰链代替传统的球面副。充分集成了并联机构、压电陶瓷和弹性铰链的优点,为多维加速度传感器的结构设计提供了一种新的思路。

(2)通过将固结在动平台(质量块)上的 3个复合弹性球铰链的运动参量作为中间变量,能够推导出并联机构正向运动学(包括位置正解、速度正解和加速度正解)的封闭解,为传感器的实时测量提供了有力保证,同时也为其他并联机构运动学、动力学的分析提供了一种有效的解决途径。

(3)通过测量 9组压电陶瓷的输出电压并运用机械多体系统动力学理论可以建立六维加速度的解耦模型。通过引入辅助角速度以及四元数,可以从系统动力学方程中分离出旋转矩阵,进而实现六维加速度的完全解耦。针对四元数的违约问题,运用矩阵广义逆理论提出了一种有效的修正算法,该算法还可以移植到速度修正、加速度修正中去,且可以重复运行,直到满足精度要求为止。

(4)通过算例,将根据数学模型计算的结果与ADAMS仿真的结果进行了对比,将六维加速度传感器实物样机的试验结果与激振器的标准输出值进行了对比,结果表明:提出的新型六维加速度传感器可以实现运动载体加速度 6个分量的实时、精确测量,有效验证了设计方案的合理性以及数学模型的可靠性。

[1] Chen JH,Lee SC,Debra D B.Gyroscope free strapdown inertial measurement unit by 6 linear accelerometers[J].Journal of Guidance,Control,and Dynamics,1994,17(2):286—290.

[2] Brown A K.GPS/INS uses low-cost MEMS IMU[J].IEEE Aerospace and Electronic Systems Magazine,2005,20(9):3—10.

[3] Touboul P,Rodrigues M,Willemenot E,et al.Electrostatic accelerometers for the equivalence principle test in space[J].Classical Quantum Gravity,1996,13:67—78.

[4] Canuto E.Drag-free and attitude control for the GOCE satellite[J].Automatica,2008,44:1 766—1 780.

[5] Abdellatif H, Heimann B. Advanced model-based control of a 6-DOF hexapod robot: A case study[J].Mechatronics,2010,15(2):269—279.

[6] Lam T L,Qian H H,Xu Y S.Omnidirectional steering interface and control for a four-wheel independent steering vehicle[J].Mechatronics,2010,15(3):329—338.

[7] Ang W T,Khosla P K,Riviere C N.Nonlinear regression model of a low-g MEM S accelerometer[J].IEEE Sensors Journal,2007,7(1):81—88.

[8] 吉训生,王寿荣.电容式硅微机械加速度计系统的特性研究 [J].宇航学报,2005,26(4):446— 450.JI Sun-sheng,Wang Shou-rong.Analysis of characteristics on capacitive silicon micro-accelerometer system[J].Journal of Astronautics,2005,26(4):446—450.

[9] 赵彦涛,李志全.基于 Bragg光纤光栅的三维加速度传感器的研究 [J].仪器仪表学报,2006,27(6):299—301.ZHAO Yan-tao,LI Zhi-quan.Study on triaxial accelerometer based on FBG[J].Chinese Journal of Scientific Instrucment,2006,27(6):299—301.

[10]Feng J. Six-axis electrostatic accelerometer[D].Texas:Texas Tech University,1995.

[11]Yuan G,Wang D H,Hou X H,et al.Rapid prototyping of a piezoelectric six-axis accelerometer[A].Proceedings of the World Congress on Intelligent Control and Automation[C].2008,6:2 723—2 726.

[12]高钟毓,董景新 ,张嵘.微机电传感器发展及应用的现状与趋势 [J].机械工程学报,2003,39(11):7— 16.GAO Zhong-yu,DONG Jing-xin,ZHANG Rong.Actuality and trend of developments and applications on micro electromechanical sensors[J].Chinese Journal of Mechanical Engineering,2003,39(11):7—16.

[13]杨廷力,刘安心,罗玉峰,等.机器人机构综合方法的基本思想、特点及其发展趋势 [J].机械工程学报,2010,46(9):1—11.YANG Ting-li,LIU An-xin,LUO Yu-feng,et al.Basic principles,main characteristics and development tendency of methods for robot mechanism structure synthesis[J].Chinese Journal of Mechanical Engineering,2010,46(9):1—11.

[14]Unruan M,Ananta S,Laosiritaworn Y,et al.Effects of parallel and perpendicular compressive stresses on the dielectric and ferroelectric properties of soft PZT ceramics[J].Ferroelectrics.2010,400(1):144—154.

[15]张宪民,王华,胡存银.压电陶瓷驱动三自由度精密定位系统的弹性动力学与输入调理特性研究 [J].振动工程学报,2007,20(1):9— 14.ZHANG Xian-min,WANG Hua,HU Cun-yin.Elastic Dynamic and input tuning analysis of a piezoelectric ceramics actuated 3-DOF compliant precision micropositioning stage[J].Journal of Vibration Engineering,2007,20(1):9—14.

[16]吴胜宝,章定国.大范围运动刚体-柔体梁刚柔耦合动力学分析 [J].振动工程学报,2011,24(1):1— 7.WU Sheng-bao, ZHANG Ding-guo. Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion[J].Journal of Vibration Engineering,2011,24(1):1—7.