论垄断与自由竞争都具有高效率
张理智
论垄断与自由竞争都具有高效率
张理智
只要不是通过超经济强制,而是通过纯粹经济活动本身产生的垄断,包括独家垄断、垄断竞争,都是既合乎正义又具有经济效率的,可简称为“垄断有效”。“反垄断”只应局限于反对由超经济强制生成的各种垄断。针对由纯粹经济活动生出的各种垄断实行“反对”、“管制”和“以政府经营取代”,都是有害无益的“逆帕累托改进”。反之,将其视作如同自由竞争一样,实行充分自由放任和保护政策,才是有益无害的“帕累托改进”。应当如同保护消费者主权一样维护纯粹经济活动中的各种垄断者主权。
垄断;寡头垄断;垄断竞争;垄断者主权;资源配置
人们普遍认为,在自由竞争、独家垄断、寡头垄断、垄断竞争这四种市场类型中,唯有自由竞争市场形成的低价格与高产量才具有最高效率。其余三种市场都会程度不同地导致以高价格、低产量为特征的低效率。因此,有必要对垄断实施“反对”、“管制”、“以政府经营取代”,以便尽可能充分实现整个社会经济的高效率 (萨缪尔森,诺德豪斯,1992)。
本文试图说明,只要不存在本来应由法制取缔的欺行霸市、欺诈、官商勾结等等超经济强制,即只要是在合法的纯粹经济活动中生成的上述四种市场类型,各自形成的价格与产量 (包括独家垄断、寡头垄断、垄断竞争市场形成的高价格与低产量),都是具有最高经济效率的。都应一视同仁地对其采取自由放任与保护政策 (包括对垄断寡头相互间之博弈与勾结也应采取自由放任与保护政策),而不应“反对”、 “管制”、或“以政府经营取代”。总之,本文试图说明,被经济学界许多人视作经济学常识的“垄断导致市场失效”这种见解不能成立。
一、独家垄断之高效率
假定X先生发明了一种能在几天内彻底治愈任何一种癌症的特效药。为简便计,假定每单位药物平均成本等于边际成本 (两者都用C表示)且C=2。再假定价格P是产量Q之函数且P=P(Q) =8-Q。(谢识予,1997)。于是可通过对PQ-2Q求导解垄断利润之最大值,得出:
P※=5 Q※=3 垄断利润R※=9
这就是人们通常所指责的独家垄断者 (这里是X先生)为追逐最高垄断利润导致的高价格、低产量以及高利润。
在此条件下,若所有消费者 (这里指所有癌症患者)与政府联合起来,对独家垄断采取反对、管制、或威胁以政府经营取代之反垄断政策、措施,逼使治癌特效药定价趋向边际收益与边际成本相等。即逼使X先生至少在一定程度上走向P=C=2。代入P=8-Q可得出Q=6。与此同时,垄断利润等于零。(PQ-2Q=2Q-2Q=0)。若种种反垄断措施彻底奏效,即导致高价格5变成低价格2,低产量3变成高产量6,高利润9变成低利润零。这当然是高效率。但却仅仅是针对癌症患者和主持反垄断的政府官员在理论上、在想象中、或仅仅在暂时可实现的虚假、空幻或短暂的高效率。
因为,一旦“反垄断”、“管制垄断”、“政府经营取代私人垄断”彻底奏效且成为既定常规政策,X先生 (或可能发明类似治癌特效药,能为人类造福的各种独家垄断产品的Y先生、Z先生等等)就会理性地被迫将特效药 (或类似独家垄断产品)转入黑市交易。黑市交易的结果是:价格与产量以及垄断利润重新回到独家垄断本来应有的唯一均衡点 (即P※=5;Q※=3;R※=9)。所不同的只是,所有消费者为在黑市上偷偷购买急需的独家垄断产品,还必须额外付出“黑市交易成本”。这显然比放任独家垄断市场自由经营效率更低,且为独家垄断者和所有消费者双方都带来为躲避官方管制被迫进行非法黑市交易的种种麻烦。
倘若官方为根治垄断而动用大量警力严防死守,彻底消灭一切黑市交易,则无异于“谋财害命”(谋X先生本来应发之财;害所有癌症患者本来可救之命),这就不仅仅是低效率,而且成了不可容忍之愚蠢。可见,对独家垄断,由“反对”、“管制”、“政府经营取代”改变为自由放任与保护,是有益无害的帕累托改进。(不言而喻,以上围绕X先生案例所述独家垄断之一般原理,可类推于由纯粹经济活动生出的任何一种独家垄断)。
二、寡头垄断
令独家垄断变成二人寡头垄断 (多于二人同理可推,不必细述)。即假定有X1、X2两位先生取代X先生,且各种条件与前述X先生设定相同。于是可求得,当 X1、X2两寡头不勾结时,P1※=P2※=4;Q1※=Q2※=2;R1※=R2※=4。若相互勾结,则P※、Q※、R※三者各自总量收敛于如同先前X先生之独家垄断。总利润 (=9)由X1、X2均分,各得4.5。X1与X2如同两囚犯博弈。最终结果 (勾结失败或勾结成功)由两人每次博弈所求得的当次纳什均衡解决定。
对待寡头垄断,为实现整个社会相关各方(包括所有寡头垄断者、全体消费者、政府官员)之最高效率,如同对待独家垄断一样,也应采取完全自由放任与保护政策。包括放任与保护寡头垄断者相互之间采取勾结策略或采取不勾结策略。当寡头之间实现成功勾结时,可将各寡头总计视作如同独家垄断之X先生。当然应采取与对待X先生相同的自由放任与保护政策。当其不勾结时,总体比独家垄断产量更高、价格更低。给全体消费者带来“白拣的便宜”。对此,政府也只应放任与保护,而不必干预。
三、垄断竞争
为叙述简便计,不妨做如下思想实验。
假定一座城市有数量众多的N家小面店星罗棋布于全城各处。每一家面店所有各种性状全部等同 (将可能存在的口岸差异也抹去不计),即形成标准的自由竞争格局。于是每家面店边际收益等于边际成本等于平均成本等于价格。
若在N家面店之旁另有一家 (且仅有一家)由W先生经营之小面店。除具有与其余N家小面店之全部相同性状外,因掌握特殊操作方法和配置特殊调料 (为论述简便,姑且假定所费各项成本为零)而使面食特别鲜美。形成具有独家特色之名小吃。诱使众多消费者趋之若鹜。于是即形成“垄断竞争”。其经济性质可用“垄断竞争图”图示如下。
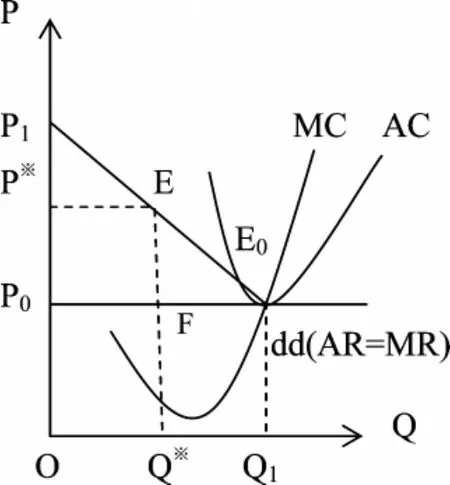
上图由两部分组成:自由竞争部分和垄断部分。
E0是所有自由竞争面店共同收敛之均衡点。均衡价格为OP0,均衡产量为OQ1。
E点是W先生在自由竞争基础上,因其面食具有独特美味而到达的能实现最大利润的垄断竞争均衡点。E点表明,均衡价格为O P※,均衡产量为O Q※。W先生所能实现的最大垄断利润由四边形 P※P0FE表达。(可以证明,当且仅当P0P※=1/2 P0P1时,垄断利润最大。证明过程从略)。
若将“垄断竞争图”中自由竞争均衡价格P0横线以下抹去不计,再加上与先前所述X先生相同的数学条件,则W先生处在E点,就如同前述X先生之独家垄断。两者之价格、产量、最大垄断利润之决定原理完全相同。
因此,“垄断竞争”内含之“垄断”,其实质是裹夹在竞争中的独家垄断。
虽然,上图中E点与E0点相比,价格更高,产量更低。但在E点却实现了消费者与垄断竞争者W先生两者之双赢。且这种双赢不可被自由竞争之E0点取代。
消费者当然有权只在N家面店消费毫无垄断特色的自由竞争面食,从而有权只获取消费者剩余三角形P1P0E0。然而,千千万万雄辩之事实表明,名小吃、名酒、名烟、名牌服装、名牌商标、名牌老字号等等诱使众多消费者为获取图中垄断竞争产品之消费者剩余P1P※E而积极趋向E点,心甘情愿通过双方平等自由交易,让诸如W先生之类垄断竞争者获得垄断竞争赢利,从而成全消费者与垄断竞争者之双赢。这岂不表明,垄断竞争,如同前述独家垄断和寡头垄断,能使权力平等之垄断者与消费者双方,通过自由交易,在均衡点实现以最大可能双赢体现的最高经济效率。
试设想,若强制所有名小吃、名酒、名烟、名牌服装、名牌商标、名牌老字号等等垄断竞争产品全都从自身收敛之高价格与低产量均衡点改而收敛于自由竞争之低价格与高产量均衡点,(例如强迫W先生从图中E点改变为E0点)。这就无异于消灭所有名小吃、名酒、名烟、名牌服装、名牌商标、名牌老字号等等。这显然是对平等自由交易双方都有害无益的“逆帕累托改进”。同时也由此证明,由反垄断 (包括反“垄断竞争之高价格、低产量”)改变为保护垄断 (包括保护“垄断竞争之高价格、低产量”)是有益无害的帕累托改进。
四、消费者主权与垄断者主权
其实,所有消费者本来都如同所有垄断者一样精明、理性。本来都有权相互勾结为一体 (即勾结合作为一个独家垄断买者),与任何一家垄断者博弈。只是由于通常预期勾结成本大大高于勾结收益,他们才放弃相互勾结 (奥尔森,1995)。在纯粹经济活动中,在不存在任何超经济强制的市场上,任何垄断者与任何消费者都具有平等的自由交易或平等的自由不交易或平等的自由博弈主权。既然任何垄断者与任何消费者通过平等自由交易都能实现双赢,则政府理应同时且平等保护双方之主权。即同时且平等保护“消费者主权”与“垄断者主权”。只有如此,才能实现整个社会最大经济效率,并同时实现各种类型垄断者与所有消费者之间的最大公平。
五、政策建议
由以上所述可知,在不存在任何超经济强制的纯粹经济活动中,自由竞争,独家垄断,寡头垄断,垄断竞争这四类市场形式,各自都具有在各自不同条件下的最高经济效率。只要买卖双方信息对称,在这四种市场上进行的任何一笔自由平等交易都可实现交易双方之最大双赢和整个社会资源配置之最优。因此,将自1890年由谢尔曼法所开创的“反垄断”、“管制垄断”、“以政府经营取代私人垄断”这三项政策彻底取消,而改变为,政府在既有专利保护政策基础上,进一步发扬光大这种保护,即进而理直气壮地:保护独家垄断、保护寡头垄断、保护垄断竞争、鼓励展开充分自由竞争。这种改变,必是“帕累托改进”。与此同时,政府所要坚决取缔者,只能限于以超经济强制为特征的既非正义又无效率之垄断。(其中包括:欺行霸市、欺诈经营、官商勾结等等)。只要如此实行且卓有成效,即可使独家垄断市场、寡头垄断市场、垄断竞争市场、自由竞争市场上的任何产品之价格与产量,都收敛于社会资源配置可能到达的最优均衡点。
〔1〕萨缪尔森,诺德豪斯.经济学〔M〕.中国发展出版社,1992.
〔2〕谢识予.经济博弈论〔M〕.复旦大学出版社,1997.
〔3〕奥尔森.集体行动的逻辑〔M〕.上海三联书店,上海人民出版社,1995.
F276.6
A
1008-9187-(2012)01-0101-03
张理智,四川省社会科学院金融研究所研究员,四川 成都 610071。
李晓南〕

