偏心轮腿六足机器人三足步态的静态稳定性分析

李君科，王宇俊，万 婷，何新强

(西南大学计算机与信息科学学院，重庆 400715)

偏心轮腿六足机器人三足步态的静态稳定性分析

李君科，王宇俊，万 婷，何新强

(西南大学计算机与信息科学学院，重庆 400715)

利用重心投影法，从偏心轮腿六足机器人的机身和三足步态的特点入手，分析了该机器人在使用三足步态行走时的特点，并论证了偏心轮腿六足机器人的三足步态具有静态稳定性的特点.

偏心轮腿六足机器人;三足步态;静态稳定性;重心投影法

0 引言

人们对于机器人的研究越来越注重它的实际使用功能，大到航空航天、宇宙探索、军事侦察和攻击，小到管道排障、疾病检查、抢险救灾等非结构环境下的自主作业［1］.在这些环境里，传统的设计方法已经不能满足现实的需求.要解决这一问题，或者改变机器人的运动方式，或者改变机器人的运动机构.

轮子的应用历史悠久，因此大多数现代机器人采用这种运动机构.但其有不足之处，就是越障能力有限，并且在坎坷不平的地面运行时，稳定性满足不了人们的期望.机器人的运动机构从轮子发展到履带，增强了它对地面的适应能力，但缺乏轮子的灵活性.在不断的探索和研究中，人们发现具有轮子特点的偏心轮腿机器人具有很好的地面适应能力，如在有辐射、有粉尘、有毒及战场环境下执行侦察任务，在地震、塌方及火灾后的废墟中找寻伤员等.本文针对笔者研制的偏心轮腿六足机器人［2－3］及其常用的三足步态进行分析，并证明其使用三足步态具有稳定性的特点，进而说明了使用三足步态的合理性.

1 偏心轮腿六足机器人的三足步态概述

根据笔者设计的偏心轮腿六足机器人并结合经典的三足步态［4－5］，构造了适合于该偏心轮腿六足机器人的三足步态，并约定如下.

(1)设定偏心轮腿有停止、支撑相和摆动相共3种状态.腿的支撑相是腿部接触地面的状态，腿处于摆动相状态是腿部抬离地面而处于空中的状态.分别用0、ω1和ω2来表示偏心轮腿的转速，0表示停止，ω1表示处于摆动相的电机速度，ω2表示支撑相的速度，它们的方向有如下规定，顺时针为“+”，为正时“+”可不写，逆时针为“－”.每只腿可以检测其触地点Q离地点P和处于支撑相的各点QP的状态.

(2)设定把偏心轮腿六足机器人的六只腿分成A、B两组.如图1所示，规定以读者的角度为准，以视线对图1的面为基准，从上到下依次为偏心轮腿机器人的左面和右面，读者的右边记为机器人的前面，左边记为机器人的后面，机器人左边的前腿(L1)、后腿(L3)和右边的中腿(R2)为A组，右边的前腿(R1)、后腿(R3)和左边的中腿(L2)为B组.

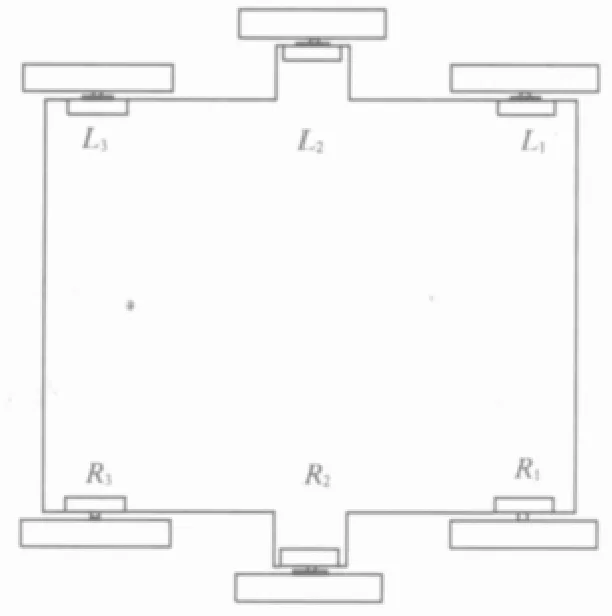
图1 机器人的方向规定Fig.1 The regulation of the robot direction

(1)初始阶段 如图2中(a)所示，A组腿Q点触地，B组腿P点触地;此时对各腿的驱动电机设置转速与方向，A组为ω2，B组为ω1，方向都为顺时针.当各腿状态如图2中的(a)时为进入第一运行阶段做准备.

(2)第一运行阶段 A组腿Q点离地，QP中的任一点触地，进入支撑相运行阶段;同时B组腿P点离地，腿上没有任何点接触地面，进入摆动相运行阶段，如图2中的(b);此时，A组各腿的转速为ω2，B组各腿的转速为ω1，方向都为顺时针;在运行过程中对各腿进行检测，如果A组中各腿的P点触地则修改参数，同样也对B组腿进行相应的检测和修改参数.此时对各腿的驱动电机设置转速与方向，A组为ω1，B组为ω2，方向都为顺时针.A组腿和B组腿状态如图2中的(c)所示时，第一运行阶段结束，进入第二运行阶段.

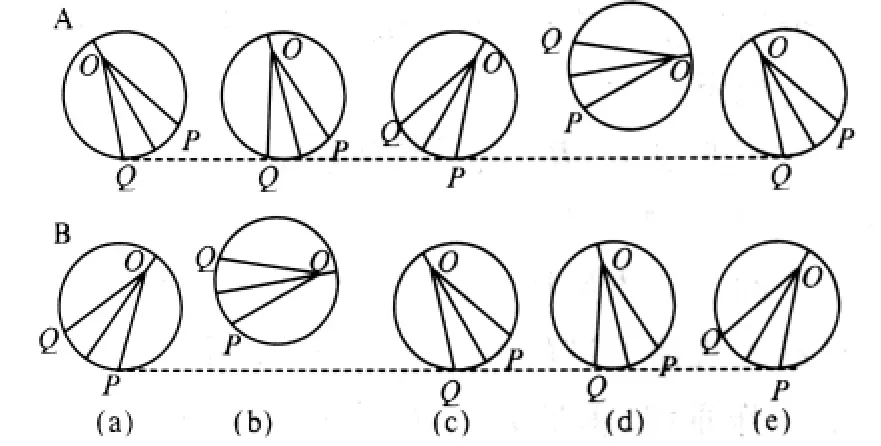
图2 偏心轮腿三足步态状态示意图Fig.2 The figure of eccentric-type legged three-foot gait state

(3)第二运行阶段 A组腿P点离地，腿上没有任一点接地，进入摆动相运行阶段;同时B组腿Q点离地QP中的任一点触地，进入支撑相运行阶段，如图2中的(d);此时，A组各腿的转速为ω1，B组各腿的转速为ω2，方向都为顺时针;在运行过程中对各腿进行检测，如果A组中各腿的P点触地则修改参数，同样也对B组腿进行相应的检测和修改参数.当轮腿状态如图2中(e)所示((e)和(a)相同)，第二运行阶段结束.

从图2可以看出，机器人经过初始状态(a)、A组支撑相和B组摆动相状态(b)、A组和B组状态相互转换状态(c)、A组摆动相和B组支撑相状态(d)，最后回到初始状态(a)，完成一个完整的运行周期，进而开始下一个运行周期.这样往复运动便实现了机器人以三足步态方式的运动.

2 三足步态的稳定性分析

我们采用经典的重心投影法(CG Projection Method)［6－7］分析六足机器人在平坦环境下的稳定性.重心投影法对机器人静态稳定步行时的稳定裕度定义为，机器人重心的水平投影至支撑多边形各边界距离的最小值.当稳定裕度Sm＞=0时，即重心落在水平投影平面内，则可以说明机器人是稳定的.重心投影法的表示为:Sm=min{Si，f，Si，l，Si，r}，其中Sm为稳定裕度，Si，f为机器人重心的水平投影到机器人支撑多边形边缘f的距离，Si，l为机器人重心的水平投影到机器人支撑多边形边缘l的距离，Si，r为机器人重心的水平投影到机器人支撑多边形边缘r的距离.

以下分析偏心轮腿机器人行走的着地点.如图3所示，设机器人的驱动轴离地高度为h，偏心轮腿圆半径为r，偏心距为e，则h=h0，h0为驱动轴心与机体底部的距离，偏心圆的圆心为O'，驱动轴的中心为O.可见，Q为偏心轮腿着地的第一点，P为偏心轮腿着地的最后一点(P、Q关于过驱动轴中心O的直径对称)，所以最大着地范围为圆弧QP.而要保证机体不与地面相碰，着地点应选择在弧QM中的某一点，其中点M为以驱动轴中心O点为起点，经过圆心O'的射线与圆弧的相交点.

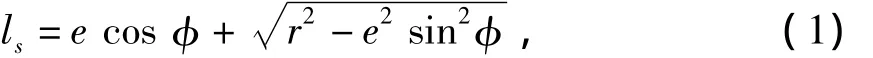
通常机器人在水平地面行走时，轴心与水平地面的距离为h并且h＞h0，线段OQ=ls为驱动轴轴心与着地点的连线，OQ的长度也就是驱动电机的转动力臂ls，且ls在水平面上的投影即O0Q0，O0为O点在水平面上的投影，Q0为Q在水平面的投影，可得驱动轴轴心O在水平面的投影O0到着地点在水平面上的投影Q0的距离d，

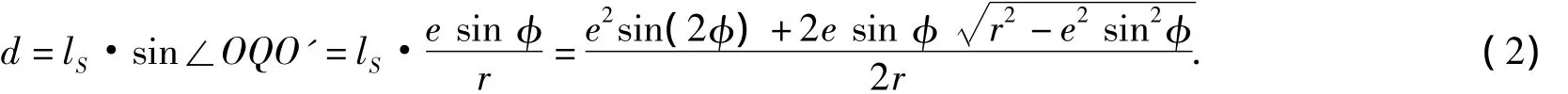
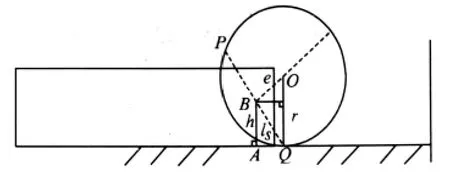
图3 最大着地点范围分析Fig.3 Analysis on the maximum landing scope

如果着力点在水平面上，则水平面上的Q0和Q重合，如果着力点不在水平面上而是在水平的障碍物上，式(1)和式(2)也适用，式(1)中的φ为OQ与OO'M的夹角.

除了龙王庙，笔者认为，船厂附近还应有衙署、军营、驿站、工棚、库房、工匠住宅、码头等设施，当然这些不可能全是刘清所建。因为刘清第一次来到船厂时，船厂已经建立整整十年了，基础设施和军政建制应该完善了，刘清对此大多是进行修缮和增扩建。

由上述分析可得

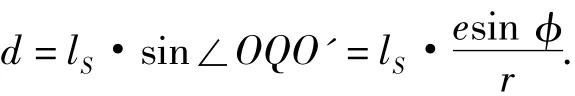
由机器人在水平地面行走的过程可知，当机器人的机身重心固定时，每只腿的方向一致，且每只腿d的最大距离为e时，机器人以三足步态行走.依重心投影法的理论可知，这时机器人是最有可能不稳定的，如果在这种情况下是稳定的，则机器人在其他任何情况下也是稳定的.下面通过重心投影法对这种最不稳定的情况进行稳重裕度分析.

我们假设L1、R2、L3三只腿触地，用A、B、C表示触地点，则三角形ABC构成一组支撑三角形.如图4所示，采用如下方法建立坐标系，机器人的重心在水平面上的投影为坐标原点O，以过O点和驱动轴R2的轴心在水平面上的投影所在的直线为X轴，以向右方向为X轴正方向.过原点作X轴的垂线，垂线为Y坐标轴，以机器人机体前进的方向为正方向.则A、B、C的坐标分别为A(xA，yA)、B(xB，yB)、C(xC，yC)，由O向AB、BC、CA作垂线，垂足E、F、D的坐标分别为E(xE，yE)、F(xF，yF)、D(xD，yD)，S1、S2、S3分别为重心投影到支撑边的距离，m为L3、R3间的宽度，m0为R3比R2多伸出的长度，l表示R1与R3的距离，e表示偏心距.

则直线AB方程为

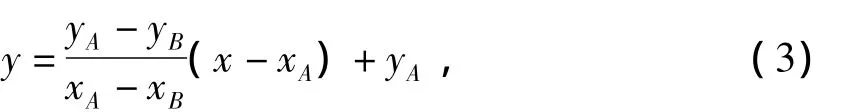
由直线OE垂直于直线AB，则直线OE的方程为

由式(3)式(4)可求出垂足E点的坐标(xE，yE)，

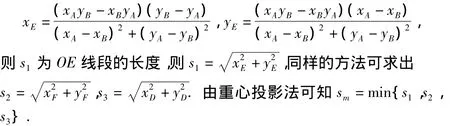
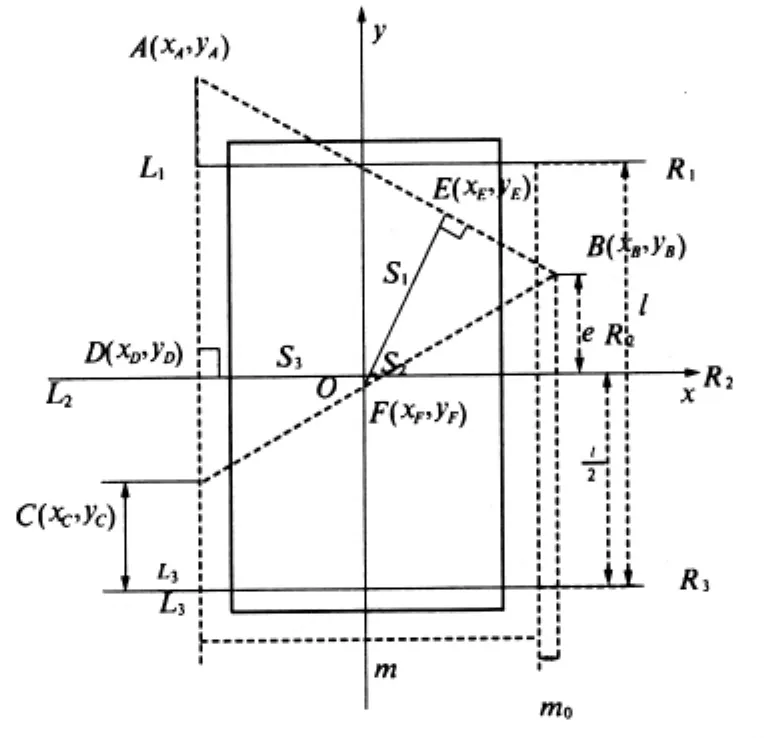
图4 三足步态稳定裕量计算图Fig.4 The stability margin calculation figure of the three-foot gait

通过以上分析并结合图4可见，S2在此状态最小，若在约束条件下有yF＜0，则机器人的重心没有落在CB外侧，所以三足步态是稳定的.

由此可得F点的纵坐标

由图4可知B点、C点坐标为

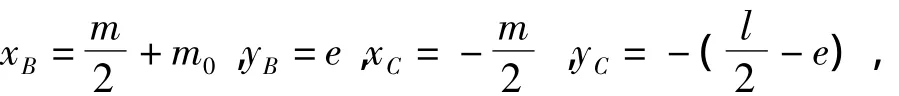
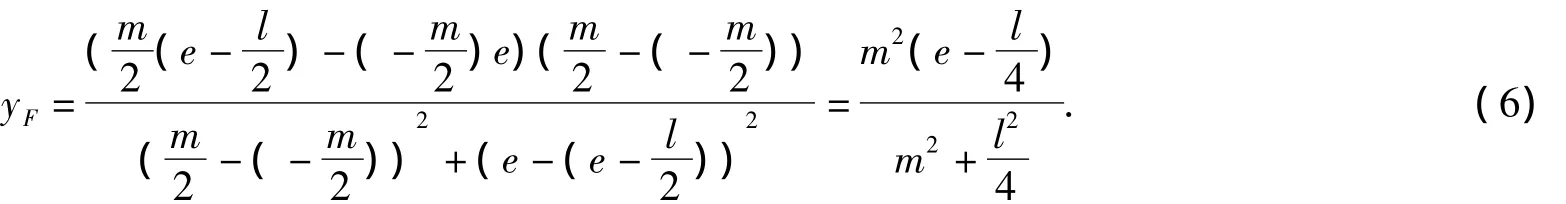
由偏心距定义可知

偏心轮腿六足机器人在整体设计约束条件为

由式(7)和式(8)可得

由式(6)和式(9)可得yF＜=0，由此可知机器人重心落在水平投影平面内，即重心的投影落在了稳定区域内，也就是说机器人的重心不会超出其支撑三角形.因为即使在最坏的状态下，重心的投影也不会超出其稳定区域，则其他状态下也不会超出稳定区域，可见偏心轮腿六足机器人以三足步态行走是稳定的.

3 实验与分析

由上面的分析可以得出结论，只要设计的六足机器人的重心在其三足步态的支撑三角形内，则机器人在平坦的地面行走时不会发生偏倒、侧重，从而使机器人保持行走稳定性.笔者设计的三足步态满足上述要求，通过机器人的行走测试发现，该机器人在行走时不会出现不稳定的情况，说明该偏心轮腿六足机器人采用的三足步态行走时满足稳定性要求.

4 结束语

多足机器人的应用越来越广泛，其行走的步态也多种多样，在设计多足机器人步态时要充分考虑其稳定性，才能使其应用到机器人当中.本文以笔者设计的偏心轮腿六足机器人为分析基础，详细分析了该机器人三足步态的稳定性，为以后的工作奠定了基础.

［1］ 谭兴军，王宇俊，何新强.基于单片机的管道机器人多路数据实时采集系统的设计［J］.工业控制计算机，2010(11):23－26.

［2］ 何新强，王宇俊，谭兴军.偏心轮腿六足机器人控制电路设计［J］.河南教育学院学报:自然科学版，2011，20(1):36－40.

［3］ 万婷，王宇俊，李君科，等.偏心轮腿六足机器人四足步态规划［J］.河南教育学院学报:自然科学版，2011，20(4):41－44.

［4］ TAN XINGJUN，WANG YUJUN，HE XINQIANG.The gait of a hexapod robot and its obstacle-surmounting capability［C］//Proc of the World Congress Intelligent Control and Automation.Taibei，2011.

［5］ KOMSUOGLU H，SOHNX K，FULL R J，et al.A physical model for dynamical arthropod running on level ground［C］//Proc of the 11th International Symposium on Experimental Robotics.Greece:Athens，2008.

［6］ MCGHEE R B.Some Finite State Aspects of Legged Locomotion［J］.Math Biosci，1968，2(1－2):67－84.

［7］ GONZALEZ D S P，JIMENEZ M A，ARMADA M A.Dynamic effects in statically stable walking machines［J］.Journal of Intelligent and Robotic Systems，1998，23(1):71－85.

Static Stability Analysis on Three-Foot Gait of Eccentric-Type Legged Hexapod Robot

LI Jun-ke，WANG Yu-jun，WAN Ting，HE Xin-qiang

(College of Computer and Information Science，Southwest University，Chongqing400715，China)

By the method of gravity center projection，from the eccentric-type legged hexapod robot’s body and the characteristics of three-foot gait，the trait of robot is analyzed when it walks with three-foot gait.The characteristics of static stability in eccentric-type legged hexapod robot’s three-foot gait is demonstrated.

eccentric-type legged hexapod robot;three-leg gait;static stability

TP242.6

A

1007－0834(2012)01－0040－04

10.3969/j.issn.1007－0834.2012.01.014

2011－12－26

李君科(1986—)，男，河南辉县人，西南大学计算机与信息科学学院在读硕士研究生.