基于多尺度方法的单晶硅纳米切削

朱朋哲， 房丰洲

(天津大学 精密测试技术及仪器国家重点实验室，天津市微纳制造技术工程中心，天津 300072)

基于多尺度方法的单晶硅纳米切削

朱朋哲， 房丰洲

(天津大学 精密测试技术及仪器国家重点实验室，天津市微纳制造技术工程中心，天津 300072)

通过在关键区域采用分子动力学(原子)描述、在远场弹性变形区域采用有限元(连续介质力学)描述建立了单晶硅纳米切削的多尺度模型。在边界区域，分子动力学和有限元互为彼此提供边界条件从而实现分子动力学区域和有限元区域的耦合。利用多尺度模型研究了单晶硅的纳米切削过程，结果表明纳米切削中工件以推挤的方式在刀具前方形成切屑。纳米切削中工件的原子键长分布、不同配位数的原子数变化和工件MD区域的原子构型的研究表明，纳米切削中发生了4配位的金刚石立方α-Si向6配位的β-Si结构的转变，即相变是纳米切削中硅的主要变形机制。该研究实现了单晶硅纳米切削的多尺度建模，为进一步探索纳米切削的微观机理提供了一种有效手段。

纳米切削;多尺度;单晶硅;相变

0 引言

纳米切削作为最重要的纳米加工技术之一，其研究日益引起各国学者的关注。目前，纳米切削技术的发展受到切削加工理论、加工工艺以及检测与评价等诸多因素的制约。在纳米切削过程中，材料去除现象发生在极小的区域，可能仅涉及到几个或几十个原子层。纳米切削加工在本质上是一个离散的过程，因此，建立在连续介质力学基础上的宏观切削理论已无法直接用于指导纳米加工实践。而分子动力学模拟(molecular dynamics simulations，MD/MDS)作为一种计算机模拟方法可以得到原子的运动轨迹，能够观察纳米切削实验中无法观测到的原子尺度的物理、力学行为，同时不受加工设备、加工条件的限制，可方便、低成本的建立加工系统，已经成为研究纳米加工机理的一种重要手段［1］。

美国的劳伦斯实验室最先用分子动力学模拟研究了纳米切削过程［2］。随后，众多学者采用MD开展了纳米切削过程的研究。Ikaw等［3］模拟了金刚石刀具对单晶铜的纳米切削过程，研究了刀具刃口半径和最小切削厚度对切屑形成过程的影响，发现当切削厚度小于刀具刃口半径时不会形成切屑。同时，他们还研究了刀具刃口半径与切削厚度的关系［4］，发现刀具刃口半径越小，切削厚度越小，最小切削厚度大约是刃口半径的1/20～1/10。Komanduri等用MD模拟了晶体方位和切削方向对单晶铝的纳米切削过程的影响［5］。Zhang等用MD研究了切削速度对铜纳米切削过程的影响［6］。Zhu等研究了各种工艺参数如刀具几何形状、切削深度、切削速度和温度对纳米切削过程的影响［7］。Fang等提出了基于推挤模型的纳米去除机理，并通过MD和纳米压痕实验进行了验证［8-9］。

尽管分子动力学模拟是研究纳米切削过程的主要手段之一，但分子动力学模拟在应用方面存在着一定的局限性，即其所能模拟的空间尺度和时间尺度有限，无法进行直接的实验验证。因此，迫切需要扩大MD模拟的规模。同时，纳米切削涉及宏观、介观和纳观尺度，是一个复杂的跨尺度问题，需要采用多尺度方法来揭示纳米切削的微观机理。在刀具和工件接触区域，采用MD精确描述，而在远离接触区域的部分可采用计算效率较高的连续介质力学(如有限元)进行描述。多尺度方法既能扩大所能研究系统的尺寸，又能揭示纳米切削过程的微观机制，成为近年来国际上研究的热点［10］。Sun 等［11］和赵等［12］利用准连续介质方法实现了单晶铜纳米切削过程的多尺度模拟。Shiari等［13］采用CAAD方法研究了单晶铝的纳米切削过程，重点研究了室温时不同切削速度下的工件材料去除、切屑形成、加工表面演化以及位错的生成和扩展。梁迎春等分别采用准连续介质方法［14］和桥域多尺度方法［15］研究了切削速度对单晶铜纳米切削过程的影响。目前采用多尺度方法研究纳米切削过程仍处于初级阶段，并且多用于研究单晶金属的纳米切削过程。

笔者基于 HSM(Hybrid Simulation Method)［16-17］建立了耦合MD和有限元的纳米切削三维多尺度模型，研究了单晶硅纳米切削中材料的变形机理。

1 模拟模型与计算方法

多尺度切削模型由刚性金刚石刀具和单晶硅工件两部分组成，如图1所示。刀具采用MD进行描述。对于工件，在刀具要经过的附近区域，可采用MD模拟进行精确描述;而远离刀具的区域原子的位移和应变梯度都较小，采用计算效率较高的有限元(FE)法描述即可。MD和FE的重叠区域是握手区(HS)。MD和 FE之间信息的传递通过握手(HS)区来实现。

图1 纳米切削的多尺度模型Fig.1 Multiscale model of nanometic cutting

工件为单晶硅，方位为x-［100］，y-［010］和z-［001］，工件尺寸为16.1 nm ×19.7 nm ×12.8 nm，MD部分尺寸为18b×10b×12b(b=0.543 2 nm，硅的晶格常数)。上表面和右侧的表面自由，其余表面采用固定边界条件。

刀具由理想的金刚石晶体生成。刀具刃口半径为2.5 nm，前角为0°，后角为10°，厚度为1.34 nm。为减少计算量，刀具是空心的。切削深度为3 nm，切削速度为200 m/s，切削沿［-100］方向进行。

1.1 分子动力学

Si原子之间的相互作用采用 Tersoff势来描述［18-19］，刀具中碳原子和工件中Si原子之间的相互作用采用Morse势来描述［18-19］。模拟中将刀具视为刚体，故刀具中碳原子间的相互作用可忽略。

原子的运动方程通过velocity-Verlet方法求解，时间步长ΔtMD=1 fs。系统初始温度为293 K，采用Langevin 热浴控制温度［20］。

1.2 有限元

工件的有限元区域变形较小，选用八结点六面体等参单元，采用线弹性本构。需要指出的是，文中为了简化，有限元部分的网格尺寸是相同的(约为0.92 nm)。实际上，变形较大的FE区域网格可以细化，而远离刀具、变形较小的区域网格可以逐渐粗化，从而进一步提高计算效率。弹性常数根据Tersoff势由单独的MD模拟得到，弹性模量为130.0 GPa，泊松比为0.28。结点运动方程由Newmark方法求解。文中在FE区域采用集中质量近似，即质量是集中分布在结点上而不是均匀分布的。单晶Si的密度是2.329 g/cm3。同MD中一样FE区域采用Langevin热浴控制温度，只要将结点看作较大的原子即可。

1.3 MD与FE的耦合

文中用握手区来连接MD和FE区域。与其他多尺度方法不同的是，该方法中握手区内原子和结点的相对位置没有限制，不需要原子和结点一一对应，因此可方便的用于模拟复杂的原子结构［16-17］。

MD和FE之间信息的传递是通过握手区的边界上MD和FE为彼此提供位移边界条件而实现的。在MD区域的边界上，原子(红色表示)的位移从FE的应变场插值得到。具体来说就是根据原子的初始位置和所在单元的形函数由结点位移插值得到原子的位移。为向MD区域提供完整的边界条件，插值原子区域的宽度必须大于Tersoff势的截断半径。这里，取工件最外面的三层硅原子即可。

FE区域的边界结点(蓝色表示)的位移是通过对其周围原子位移的空间和时间平均得到的。空间平均是在半径rav=0.3 nm的球内进行的。由于选用了线性单元，在求边界结点位移过程中采用这样的权重函数:权重随着距离的增大而线性的减小，在最大半径处权重为0。计算表明，当球的半径rav在0.3～0.5 nm(近似为有限元网格尺寸的一半)之间变化时，对模拟结果基本没有影响。由于FE区域选用的是等参单元，需要用到初始原子位置对应的局部坐标，故用到了等参逆变换［17］。

多尺度方法在MD和FE区域可采用不同的时间步长。由于每个FE结点对应着多个原子，FE区域的时间步长ΔtFE可以更大，取ΔtFE=20ΔtMD。

2 结果与讨论

图2所示为切削距离为5 nm时工件的位移场，图3为不同切削距离时的构型图。从图2和3中可以看到从MD区域到FE区域变形是连续的，纳米切削过程中变形信息逐渐从MD区域传递到FE区域，说明多尺度模型实现了MD和FE区域的有效耦合［15，17］。

图2 切削距离为5 nm时的位移场(y＞0)Fig.2 Displacement field for a half-slice of substrate(y＞0)at scratching distance of 5 nm

图3 不同切削距离时的构型Fig.3 Snapshots of configuration at different cutting distance

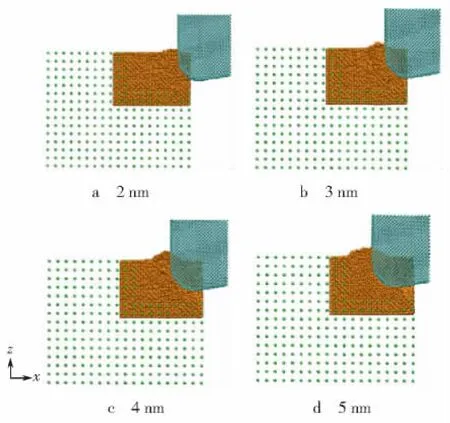
图4 不同切削距离时的构型(y＞0)Fig.4 Snapshots of configuration at different cutting distance(y＞0)

图4所示为不同切削距离时的构型(y＞0)，可以看到，纳米切削过程中切屑是由刀具的推挤作用形成的［8-9］。

图5所示为切削加工前后工件原子键长的变化。在切削之前，工件中键长为2.35 Å的原子数达到了最大值，说明此时工件为金刚石立方结构(α-Si)。切削之后，工件中出现了键长为2.43 Å和2.58 Å的原子，对应着β-Si结构。图5说明切削过程中单晶硅工件发生了α-Si到β-Si的相变［18-19］。

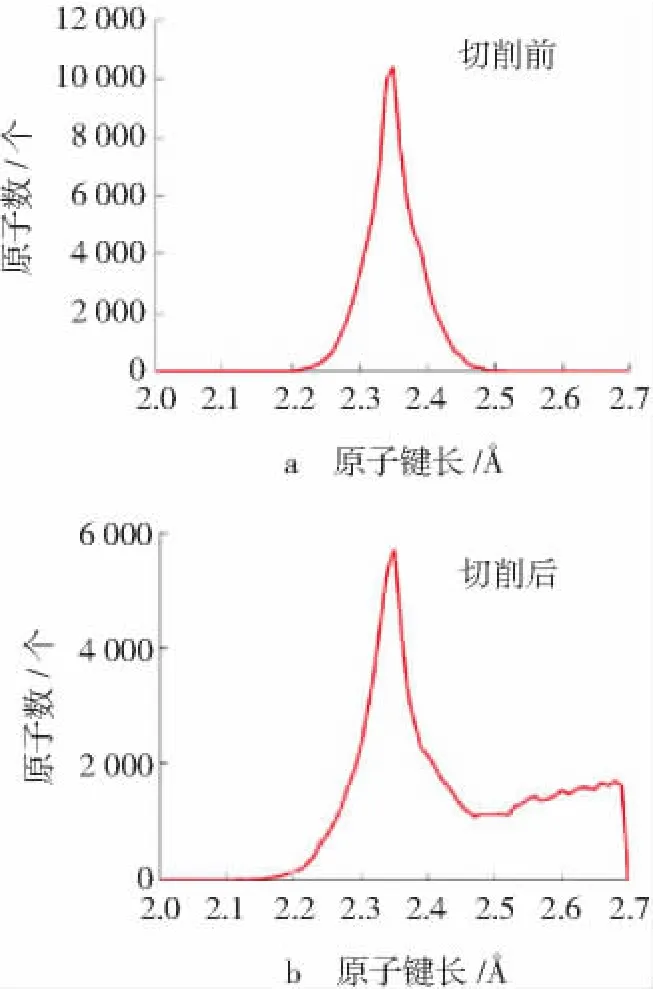
图5 工件中原子键长的变化Fig.5 Variation of atomic bond length of workpiece

为进一步研究切削中工件结构的变化，笔者分别记录了切削中具有不同配位数(成键原子的数量)的原子数量的变化和不同切削距离时工件MD区域的原子构型，如图6和7所示。切削初始阶段，工件发生弹性变形，没有相变产生。随着切削的继续进行，3配位、5配位和6配位的原子数开始增加而4配位的原子数逐渐减少。这进一步表明切削中发生了金刚石立方结构的α-Si(4配位)向β-Si的转变(β-Si的理论配位数为6)。3配位的原子是由表面效应产生的，而5配位原子可视为α-Si到β-Si相变的中间状态［21］。从图7中可以看到，5配位和6配位的原子嵌入在4配位的原子海中。7配位的原子表示完全无定形的结构［22］。

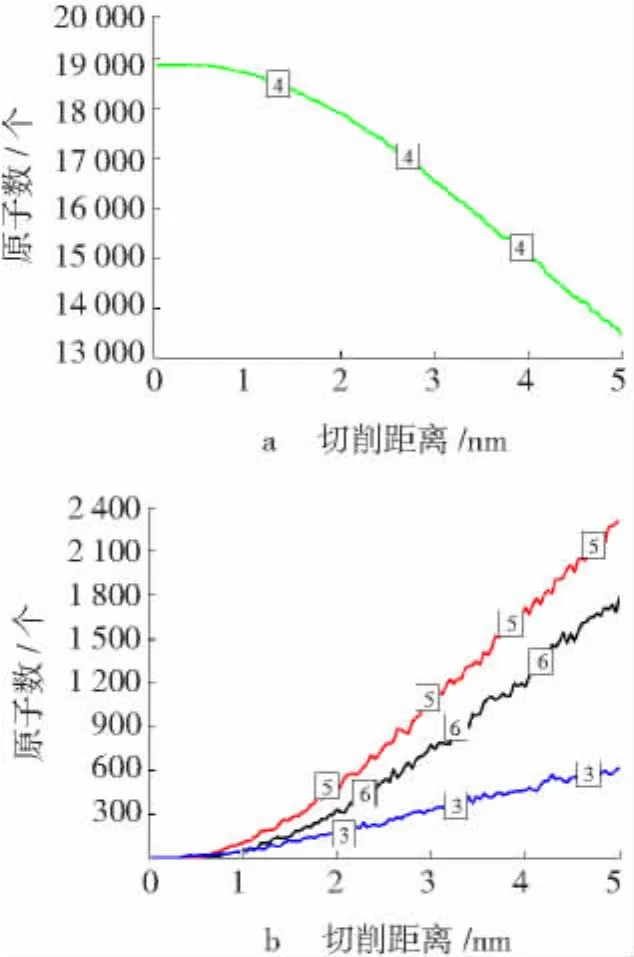
图6 工件在切削过程中不同配位数的原子数随切削距离的变化Fig.6 Variation of number of atoms of workpiece with specified nearest number of neighbors during cutting process

由于有限元的计算时间相对于分子动力学来说可以忽略不计，故采用多尺度方法，既能研究纳米切削的微观过程，又能提高计算效率，扩大所能模拟的系统的尺寸，从而使多尺度方法成为研究纳米切削过程的理想手段。

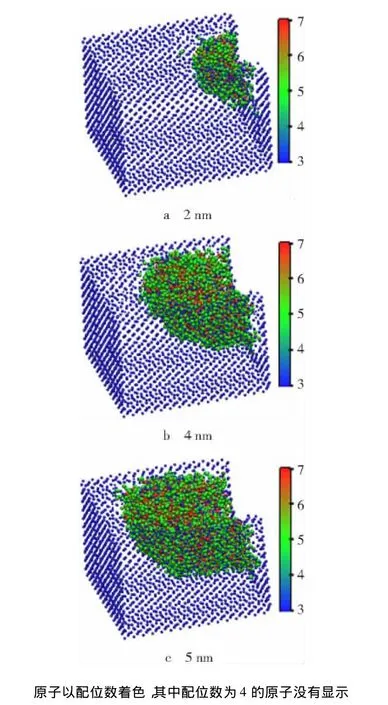
图7 不同切削距离时工件MD区域的原子构型Fig.7 Snapshots of configuration of MD region of workpiece at different cutting distance

3 结论

通过对关键区域采用分子(原子)动力学描述，在远场弹性变形区域采用有限元(连续介质力学)描述建立了单晶硅纳米切削的多尺度模型。握手区边界上的分子动力学区域和有限元区域为彼此提供边界条件从而实现分子动力学区域和有限元区域的耦合。该多尺度方法中握手区内原子和结点的相对位置没有限制，不需要原子和结点一一对应，可方便地用于模拟复杂的原子结构。

利用多尺度模型研究了单晶硅的纳米切削过程。结果表明，纳米切削中以推挤的方式在刀具前方形成切屑，硅工件中发生了4配位的金刚石立方α-Si向6配位的β-Si结构的转变，即相变是纳米切削中硅的主要变形机制。

文中所建立的单晶硅纳米切削多尺度模型，为进一步探索纳米切削的微观机理提供了一种有效手段。

［1］袁巨龙，张飞虎，戴一帆，等.超精密加工领域科学技术发展研究［J］.机械工程学报，2010，46(15):161-177.

［2］BELAK J，STOWERS I F.A molecular dynamics model of the orthogonal cutting process［J］.Proc Am Soc Prec Eng，1990，76-79.

［3］IKAWA N，SHIMADA S，TANAKA H.Minimum thickness of cut in micromachining［J］.Nanotechnology，1992，3:6-9.

［4］SHIMADA S，IKAWA N，OHMORI G，et al.Feasibility study on ultimate accuracy in microcutting using molecular dynamics simulation［J］.CIRP Annals，1993，42(1):91-94.

［5］KOMANDURI R，CHANDRASEKARAN N，RAFF L M M D.Simulation of nanometric cutting of single crystal aluminum-effect of crystal orientation and direction of cutting［J］.Wear，2000，242(1/2):60-88.

［6］ZHANG J J，SUN T，YAN Y D，et al.Molecular dynamics study of scratching velocity dependency in AFM-based nanometric scratching process［J］.Materials Science and Engineering:A，2009，505(1/2):65-69.

［7］ZHU P Z，HU Y Z，MA T B，et al.Study of AFM-based nanometric cutting process using molecular dynamics［J］.Applied Surface Science，2010，256:7160-7165.

［8］FANG F Z，VENKATESH V C.Diamond cutting of silicon with nanometric finish［J］.CIRP Annals，1998，47(1):45-49.

［9］FANG F Z，WU H，LIU Y C.Modelling and experimental investigation nanometric cutting of monocrystalline silicon［J］.International Journal of Machine Tools＆ Manufacture，2005，45(1):1681-1686.

［10］MILLER R E，TADMOR E B.A unified framework and performance benchmark of fourteen multiscale atomistic/continuum coupling methods［J］.Modelling Simul.Mater Sci Eng，2009，17:1-53.

［11］SUN X Z，CHEN S J，CHENG K，et al.Multiscale simulation on nanometric cutting of single crystal copper［J］.Proc Inst Mech Eng Part B:J Eng Manuf，2006，220(7):1217-1222.

［12］赵 晟，江五贵.纳米尺度下切削过程的准连续介质力学模拟［J］.摩擦学学报，2009，29(6):505-511.

［13］SHIARI B，MILLER R E，KLUG D D.Multiscale simulation of material removal processes at the nanoscale［J］.Journal of the Mechanics and Physics of Solids，2007，55:2384-2405.

［14］PEN H M，BAI Q S，LIANG Y C，et al.Multiscale simulation of nanometric cutting of single crystal copper-effect of different cutting speeds［J］.Acta Metallurgica Sinica(English Letters)，2009，22:440-446.

［15］梁迎春，盆洪民，白清顺，等.基于桥域理论的Cu单晶纳米切削跨尺度仿真研究［J］.物理学报，2011，60(10):100-205.

［16］LUAN B Q，HYUN S，MOLINARI J F，et al.Multiscale modeling of two-dimensional contacts［J］.Phys Rev E，2006，74:46-71.

［17］ZHU P Z，HU Y Z，FANG F Z，et al.Multiscale simulations of nanoindentation and nanoscratch of single crystal copper［J］.Applied Surface Science，2012，258(10):4624-4631.

［18］CHEONG W C D，ZHANG L C.Molecular dynamics simulation of phase transformations in silicon monocrystals due to nano indentation［J］.Nanotechnology，2000，11:173.

［19］TANG Q H，CHEN F H.MD simulation of phase transformations due to nanoscale cutting on silicon monocrystals with diamond tip［J］.J Phys D:Appl Phys，2006，39:3674-3679.

［20］ADELMAN S A，DOLL J D.Generalized langevin equation approach for atom-solid-surface scattering-general formulation for classical scattering off harmonic solids［J］.J Chem Phys，1976，64:2375-2388.

［21］MYLVAGANAM K，ZHANG L C.Effect of oxygen penetration in silicon due to nano-indentation［J］.Nanotechnology，2002，13:623-626.

［22］SANZ-NAVARRO C F，KENNY S D，SMITH R.Atomistic simulations of structural transformations of silicon surfaces under nanoindentation［J］.Nanotechnology，2004，15:692-697.

Study on nanometric cutting process of single crystal silicon based on multiscale method

ZHU Pengzhe，FANG Fengzhou

(State Key Laboratory of Precision Measuring Technology＆ Instruments，Centre of Micro Nano Manufacturing Technology，Tianjin University，Tianjin 300072，China)

This paper features the development of Multiscale model of nanometric cutting of single crystal silicon by treating the critical region with MD(atomistic description)and capturing“far-field”elastic deformations using FE(continuum description).A HS region is used to couple the MD and FE regions.At the edge of HS region each description provides displacement boundary conditions for the other to realize the concurrent multiscale simulation.The investigation into Nanometric cutting process of single crystal silicon using the multiscale model shows that during nanometric cutting of single crystal silicon，the chip in front of the tool is formed by extrusion.Investigations of the distributions of atomic bond length，the variations of number of atoms with specified nearest number of neighbors，and the atomic configurations of MD region of the workpiece reveal that there occurs a phase transformation from four fold coordinated diamond cubic phase(α -Si)to the six fold coordinated β -Si during the nanometric cutting process，namely the conclusion that phase transformation is the dominant deformation mechanism of single crystal silicon during the nanometric cutting process.The study marked by the development of the multiscale model of nanometric cutting of single crystal silicon provides an effective tool for further exploring the microscale mechanisms of nanometic cutting.

nanometic cutting;multiscale;single crystal silicon;phase transformation

TB383∶TG50

A

1671-0118(2012)04-0348-06

2012-05-30

国家重点基础研究发展计划(973计划)项目(2011CB706703);国家自然科学基金纳米制造重大计划重点项目(90923038)

房丰洲(1963-)，男，黑龙江人，教授，博士生导师，研究方向:超精密加工基础理论与技术，E-mail:fzfang@gmail.com

(编辑 晁晓筠)