基于粘聚区模型的推进剂开裂数值仿真

韩 波，鞠玉涛，许进升，周长省

（南京理工大学 机械工程学院，南京210094）

固体火箭发动机装药在生产、运输和使用过程中会承受到各种复杂载荷的作用，在这些载荷作用下装药表面可能会产生微裂纹，裂纹的萌生和发展会影响发动机内弹道性能和发动机的使用安全性，因此建立推进剂裂纹扩展过程的数值仿真方法十分重要.目前国内针对推进剂断裂过程的数值仿真尚不能准确模拟裂纹扩展过程中的应力分布、裂纹走向和裂纹终止问题.目前模拟材料裂纹扩展过程有虚拟裂纹闭合技术（VCCT）、扩展有限元法（XFEM）和粘聚区模型（CZM）等多种方法.VCCT需要事先设定材料的裂纹扩展路径，后两者可以模拟裂纹走向未知情况下的裂纹扩展问题.CZM是一种基于能量平衡和材料损伤的裂纹扩展模型，裂纹在扩展过程中裂尖材料产生损伤，其力学性能下降，当裂纹消耗能量等于裂纹扩展能时，裂尖材料失效扩展.裂尖材料的损伤避免了裂尖应力的奇异性.国外自20世纪90年代开始在粘聚区模型方面开展了大量的研究工作，国内相关学者近几年也开始展开相应的研究工作[1，2].本文使用粘聚区模型建立复合固体推进剂裂纹开裂过程的物理和数学模型，并结合ABAQUS用户自定义单元开发技术实现对复合固体推进剂裂纹扩展过程的数值仿真，以期为推进剂装药结构完整性及安全性分析提供理论支持.

1 物理数学模型

1.1 粘聚区本构模型

粘聚区模型的提出起源于DUGDALE的条状屈服区模型和BARENBLAT提出的内聚力模型.随着粘聚区理论的发展，之后又提出了各种形式的裂尖粘聚区应力分布模型，并且在沥青、金属等材料上取得了成功应用.粘聚区模型（图1所示）中材料的实际裂尖位于裂尖损伤位移δc处，假设的损伤裂尖位于损伤应力最大处.为了准确描述裂尖的损伤应力变化情况，需要建立裂尖损伤应力和损伤位移之间的对应关系——粘聚区模型本构.

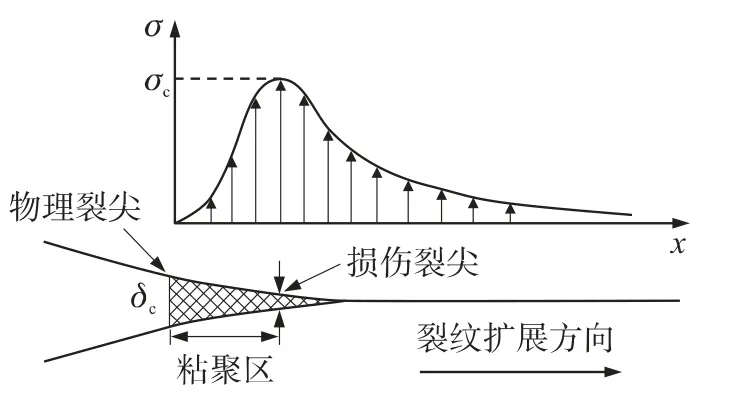
图1 粘聚区模型示意图

国外有许多学者提出了不同的粘聚区本构形式，主要有指数势函数形式、多项式形式、线性形式.其中线性粘聚区本构通过合理调整本构参数可以有效避免人工柔量问题，并且在粘弹性沥青材料上获得了成功应用[3，4].图2为线性粘聚区模型示意图.在二维情况下，材料裂尖非线性区的裂纹张开有效位移和有效应力定义为

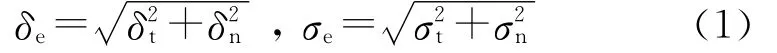
式中，δt和δn为裂尖的切向和法向位移，σt和σn为裂尖的切向和法向应力.线性粘聚区模型中假设有效位移和有效应力关系呈现为2个线性阶段，如图2所示，其中σmax为材料的应力损伤初始值；δcc为材料的损伤初始位移；δc为材料开裂的最终扩展位移；Gc为材料的断裂能，即图2中三角形面积.当裂尖材料的有效应力σe达到损伤应力σmax后，材料承载能力下降，当裂尖材料总扩展位移达到δc时，其消耗的能量等于材料的断裂能Gc，之后材料发生完全断裂.

图2 线性粘聚区本构示意图

线性粘聚区本构的具体表达形式为

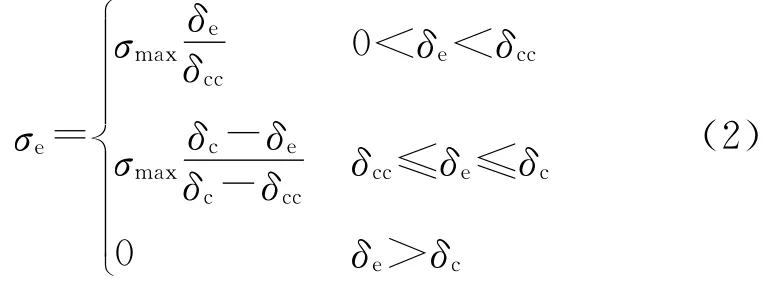
粘聚区模型的引入使有限元模型中增加了人工柔量项，造成了整体结构刚度下降.为了便于讨论，以图3所示的结构为例，上下为2个正常的实体单元，中间加入粘结单元.实体单元初始长度为d，粘结单元初始厚度为0.在载荷F作用下单元沿上下方向伸长，实体单元伸长Δ，粘结单元伸长Δc.设实体单元和粘结单元刚度分别为Ks和Kc，Es为实体单元的模量.

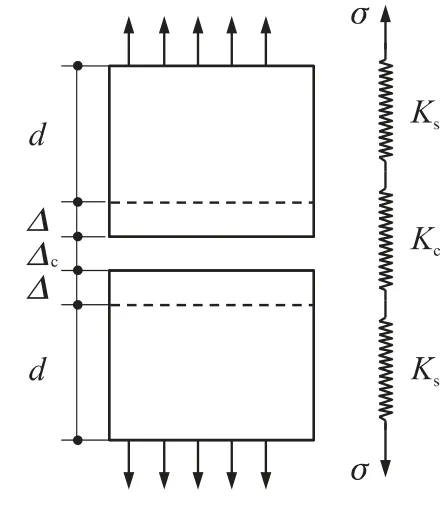
图3 粘结单元柔量分析示意图

在粘结单元未损伤前，由力平衡方程可得：

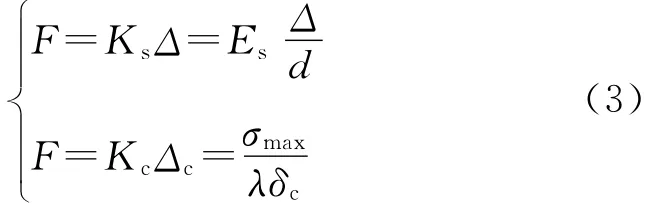
式中，λ＝δcc/δc，该结构的整体刚度为

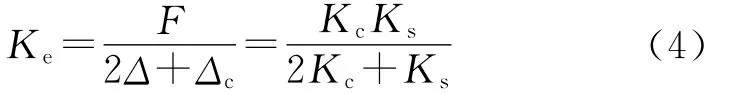
不加粘结单元的理论刚度为Ki＝Ks/2，由式（3）、式（4）得：

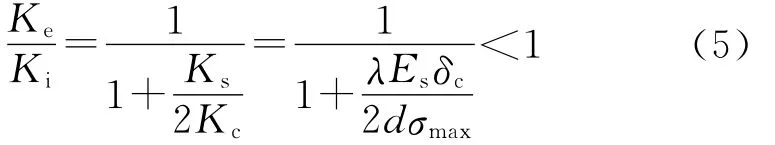
从式（5）可以发现，整体刚度与基体材料的模量Es、网格大小d、粘聚区本构参数δc、σmax和λ相关，其中Es，δc和σmax为材料的固有属性，不可改变.增大网格可以增大系统的刚度，但是会造成计算精度的下降.λ表征了粘聚区本构中初始上升段的斜率，通过减小λ可以提高粘结单元的初始刚度，从而有效避免过大的人工柔量带来的问题.λ的选择可以通过加入粘结单元和未加入粘结单元情况下的仿真结果对比确定，λ的取值应保证粘结单元的加入不会对材料未产生损伤前的系统刚度产生较大影响，从而保证计算模型具有合理的精度.

1.2 推进剂本构模型

HTPB推进剂是一种典型的粘弹性材料，在推进剂装药结构完整性分析中广泛采用线性粘弹性本构模型，该模型可以较好地反映推进剂的力学特性，因此本文在计算中使用线粘弹性本构模型.线粘弹性材料的本构方程可以写成：

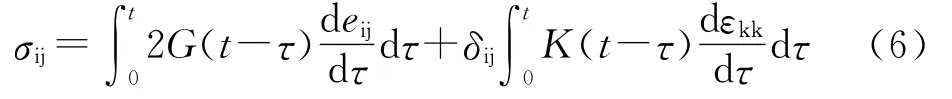
式中，G（t）和K（t）为剪切模量和体积模量，可表示为

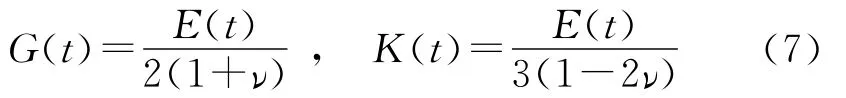
式中，E（t）为杨氏松弛模量，ν为泊松比.E（t）可以写成Prony级数的形式：

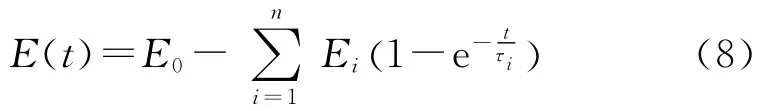
式中，τi为Prony级数中的松弛时间.

2 有限元离散及仿真方法研究

ABAQUS提供了丰富的材料和单元库，但是ABAQUS材料和单元库中并不包含特定粘聚区模型和本构关系，需要用户进行开发.ABAQUS提供了用户自定义单元的接口程序UEL，用户可以根据需要自定义各种新单元.下面以二维粘聚区模型为例，给出ABAQUS二次开发所需增量形式的粘聚区单元建立过程.由有限元理论可知，利用Newton－Raphson法求解非线性有限元问题时需要给定单元的切线刚度矩阵KT和节点平衡矢量列阵R.

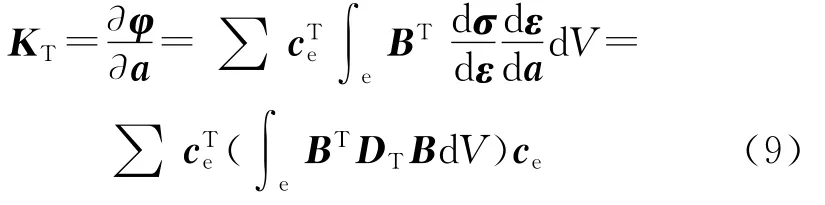
Newton法的迭代公式为

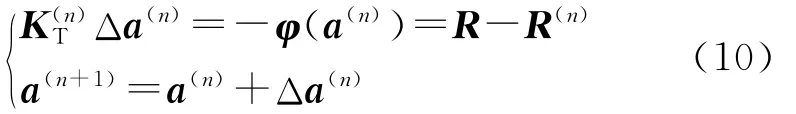
式中，

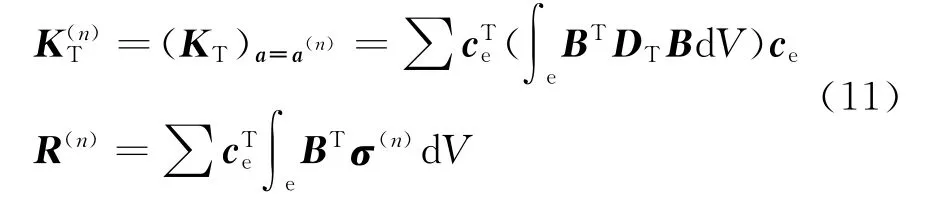
式中，ce为单元选择矩阵，a为单元位移向量，V为被积单元体积，σ为单元应力.

材料的Jacobian矩阵定义为

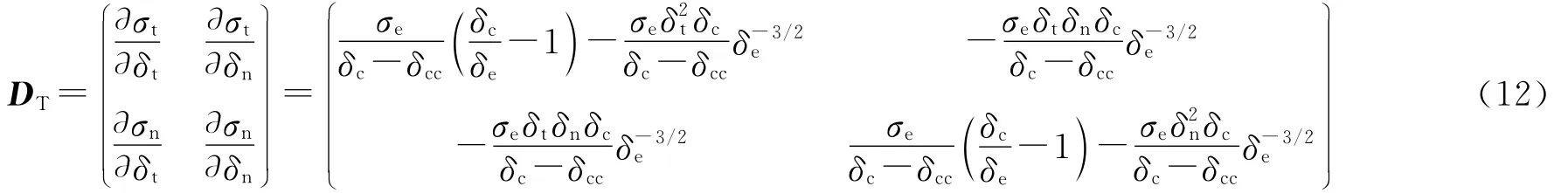
图4为2个平面三角形单元和一个粘结单元变形示意图.

单元节点1、4和2、3之间的相对位移为

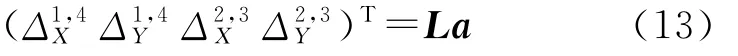
单元的积分点法向和切向位移表示为

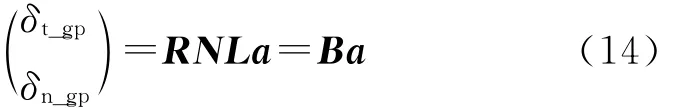
式中，a为图3中节点在系统坐标下的坐标值，R为坐标转换矩阵，N为插值形函数.

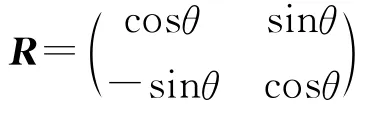
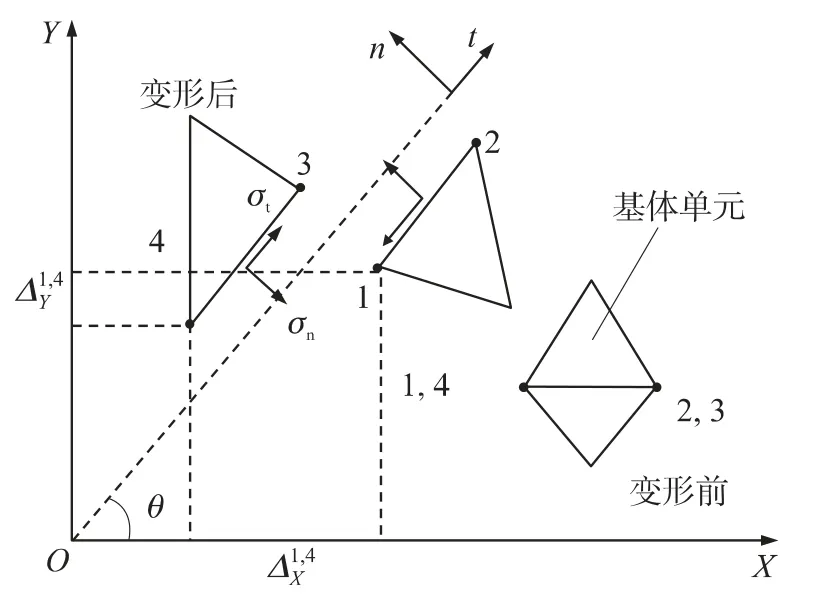
图4 粘结单元

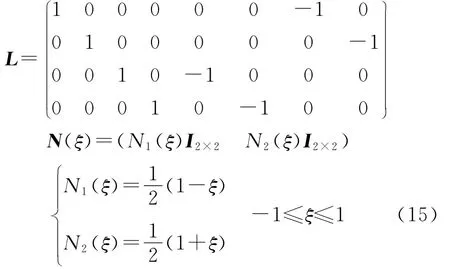
式中，ξ为变换后的坐标.

本文根据上述数学模型编制了ABAQUS用户自定义单元开发程序UEL，建立了复合推进剂裂纹扩展数值仿真方法.

3 仿真与分析

3.1 仿真模型

为了验证本文所建立的仿真计算方法的可行性，利用文献[6]中的模型，对 HTPB推进剂Ⅰ－Ⅱ型裂纹进行了数值仿真计算，图5为仿真模型示意图.模型宽度W＝50 mm，长度H＝100 mm，中心裂纹长度l＝20mm.药柱下表面固定，上表面施加60mm/min等速拉伸载荷.HTPB推进剂松弛模量通过松弛实验获取，Prony级数参数见表1，初始模量E0＝15 MPa，泊松比取0.499.粘聚区本构使用式（3）所示的形式，本文主要研究 HTPB复合推进剂的裂纹扩展有限元计算方法，粘聚区本构参数的具体实验获取不在本文研究范围之内.根据单轴拉伸实验，裂尖损伤应力σmax大致取0.5 MPa，推进剂断裂能Gc根据文献[5]大致取500J/m2.

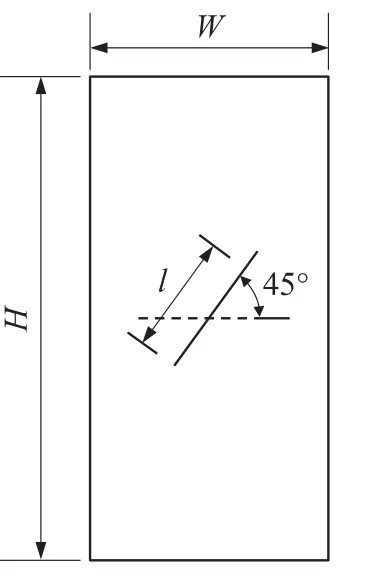
图5 仿真模型示意图

表1 松弛模量数据

使用粘聚区模型模拟裂纹扩展方向未知情况下的材料开裂过程需要在正常实体单元之间加入粘结单元，通过ABAQUS CAE无法实现.本文采用MATLAB编程语言生成包含粘结单元和二维实体单元的有限元网格.如图6所示，生成的网格中包含10 475个粘结单元和7 052个三角形实体单元.为了准确模拟裂纹扩展过程中的应力、应变变化情况，在预测的裂纹扩展路径四周进行了网格细化.

图6 有限元网格

3.2 仿真结果分析

为了确定合理的λ以避免人工柔量的影响，本文对比了无粘结单元情况下和加入了粘结单元情况下的仿真计算结果，如图7所示，图中，Fs为图6中有限元模型计算的上下表面拉力.

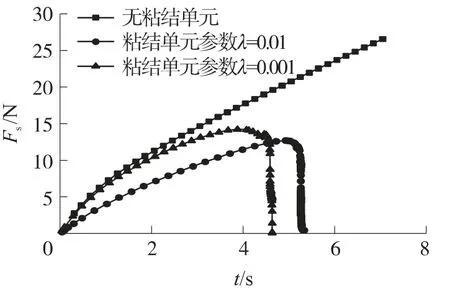
图7 不同λ下的载荷－时间曲线

从图7可以发现λ的值明显影响了计算所得的载荷－时间曲线.当不插入粘结单元时，载荷随时间持续上升，推进剂不会产生断裂.粘结单元的引入可以计算出推进剂从裂尖产生局部损伤直至断裂的整个过程.当λ＝0.01时，从图上可以看出粘聚区模型计算结果和无粘聚区模型下的计算结果相差很大，其裂纹未扩展前的曲线斜率明显低于后者，这是由于过大的人工柔量导致了系统刚度的下降.当λ＝0.001时，在3s之前粘聚区模型的使用与否对计算结果影响不大，说明该值可以较好地反映粘聚区本构模型和裂纹扩展的基本规律.在3s之后由于推进剂裂尖损伤的产生，材料承载能力开始下降，此时常规有限元方法已经不能反映出裂纹的扩展过程.在4.56s时载荷达到最大值，之后推进剂失稳快速开裂.

图8和图9为在λ＝0.001情况下，3.07s和4.56s时的有限元网格变形情况.在3.07s时推进剂裂尖开始产生了应力损伤情况，此时裂纹将要产生扩展，损伤裂尖位于裂尖的初始位置.从图7上可以看出4.56s时仿真模型所受到的载荷达到最大值.对比图9，发现推进剂产生了明显的扩展裂纹，损伤裂尖位置基本上达到了推进剂的边缘，此时推进剂的真实裂尖并不位于损伤裂尖，推进剂仍能承受外载荷的作用，但是与未受损伤前相比其承载能力已经明显下降.

图8 3.07s有限元网格

图9 4.56s有限元网格

图10为仿真和文献[6]中实验获得的拉伸破坏后的HTPB推进剂裂纹扩展路径.通过实验获得的初始裂纹起裂角平均值为51.9°，之后裂纹扩展方向转变为平直裂纹，而仿真所获得的初始裂纹起裂角约为62°，之后裂纹转变为平直裂纹.由于粘聚区有限元仿真中裂纹沿单元界面开裂，裂尖的网格细密程度决定了仿真获得的初始裂纹扩展角精度.本文仿真所获得的初始裂纹扩展角与实验结果的差距部分主要是由裂尖网格划分精度导致.

图10 仿真和实验开裂路径

文献[6]中观察到“裂纹初始扩展后都有向横向裂纹的转变趋势”，仿真结果也出现裂纹初始扩展之后转变为横向裂纹的现象.图10中的裂纹扩展路径基本重合，表明粘聚区模型可以较好地预测HTPB复合裂纹的裂纹扩展路径.

图11为裂纹扩展路径上距离初始裂尖不同位置处的Von Mises应力－时间曲线，所示的几条曲线均呈现出先增大后减小的形状，曲线的峰值对应损伤裂尖到达该点的时间.从图上可以看出裂尖位置随时间的变化情况，图中4个位置达到应力最大值的时间间隔呈现出逐渐缩小的趋势，这说明裂纹呈现出加速扩展的趋势.

本文建立了一种复合固体推进剂开裂过程数值仿真方法，为了能更加准确地描述出复合推进剂的裂纹扩展过程，需要通过大量的实验建立起准确的推进剂粘聚区模型，这也是笔者下一阶段的工作目标.

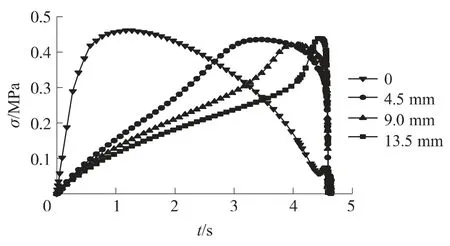
图11 裂尖扩展路径上不同位置的应力－时间曲线

4 结论

本文采用粘聚区模型理论针对复合固体推进剂裂纹扩展过程进行了研究，建立了针对推进剂断裂过程的物理和数学模型，并编制了ABAQUS二次开发程序，实现了对固体推进剂Ⅰ－Ⅱ型复合裂纹扩展过程的数值仿真计算，得到了如下结论：

①使用粘聚区模型可以很好地模拟出复合固体推进剂裂尖的损伤应力场、裂纹扩展路径和裂纹体开裂过程.

②粘聚区模型可以为固体推进剂装药完整性和安全性分析提供一种可靠的分析计算方法.

[1]刘陆广，欧卓成，段卓平，等.混凝土动态断裂数值模拟[J].兵工学报，2010，31（6）：741－745.LIU Lu－guang，OU Zhuo－cheng，DUAN Zhuo－ping，et al.Simulation of concrete dynamic fracture[J].Acta Armamentarii，2010，31（6）：741－745.（in Chinese）

[2]崔浩，李玉龙，刘元镛，等.基于粘聚区模型的含填充区复合材料接 头 失 效 数 值 模 拟 [J].复 合 材 料 学 报，2010，27（2）：161－168.CUI Hao，LI Yu－long，LIU Yuan－yong，et al.Numerical simulation of composites joints failure based on cohesive zone model[J].Acta Materiae Composite Sinica，2010，27（2）：161－168.（in Chinese）

[3]SONG S H，PAULINO G H，BUTTLAR W G.A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material[J].Engineering Fracture Mechanics，2006，73（18）：2 829－2 848.

[4]SONG S H，PAULINO G H，BUTTLAR W G.Simulation of crack propagation in asphalt concrete using an intrinsic cohesive zone model[J].Journal of Engineering Mechanics，2006，132（11）：1 215－1 223.

[5]MAROM G，HAREL H，ROSNER J.Fracture energies of composite propellants[J].Jounal of Applied Polymer Science，1977，21（6）：1 629－1 634.

[6]张亚，强洪夫，杨月诚.国产 HTPB复合固体推进剂Ⅰ－Ⅱ型裂纹断裂性能实验研究[J].含能材料，2007，15（4）：359－361.ZHANG Ya，QIANG Hong－fu，YANG Yue－cheng.Fracture behavior of HTPB composite propellant inⅠ－Ⅱ mixed mode crack[J].Chinese Journal of Energetic Materials，2007，15（4）：359－361.（in Chinese）