具有非线性扰动运动特性的高超声速飞行器动态特性分析方法

方 群，王 乐，孙 冲

（西北工业大学 航天学院，西安710072）

美国空军于2010年成功试验了X－37B“轨道试验飞行器”（Orbit Test Vehicle，OTV）和 X－51A 高超声速飞行器，这意味着能提供即时全球打击（Prompt Global Strike，PGS）能力的高超声速飞行器将越来越受到青睐.面对高超声速飞行器的高动态飞行环境，寻求合理的动态特性分析方法至关重要.CHAVEZ和 SCHMIDT[1～3]提出了基于牛顿激波理论计算气动力的通用高超声速飞行器的动力学分析方法，并以此为基础给出了飞行器稳定矩阵和控制矩阵的计算方法，不过其动态特性分析中仍采用小扰动线性化理论的分析方法.TARPLEY[4]针对未组合发动机的楔形高超声速飞行器提出了高超声速活塞理论，将线性化活塞理论推广到高超声速飞行器的动态特性分析中.目前对于常规飞行器动态特性分析的线性化方法，由于在建立模型时，为了得到线性的扰动运动模型，从而以小扰动为前提，忽略了参数偏差的高阶项，这造成了高动态环境下扰动运动模型的不准确，因此对于解决高动态飞行环境下的飞行器稳定性、操纵性分析和稳定域判定等问题，目前现有的方法并不能得到令人满意的结果.由公开发表的资料发现，现阶段对高超声速飞行器动态特性的研究中，没有特别针对高动态飞行环境的分析方法.针对高超声速飞行器在高动态环境下的动态特性分析问题，本文提出了含有参数偏差二次高阶项的非线性扰动运动模型的建立方法，并借鉴常微分方程理论在生态、电力、生物工程等领域非线性系统的应用，给出了非线性纵向扰动运动稳定性分析方法；通过 Matlab/Simulink平台的仿真，与小动态飞行环境下一阶线性化处理方法的分析结果进行对比，验证了该方法的可行性.

1 带有高阶项的非线性运动建模

1.1 非线性扰动运动建模方法

不失一般性，根据文献[5]可以得到飞行器偏量微分方程的一般形式为

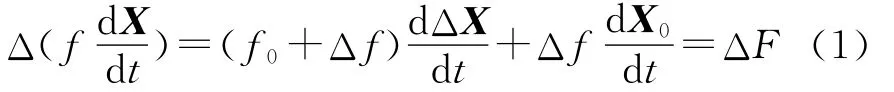
将式（1）中的函数 Δf在x10，x20，…，xn0点附近展开泰勒级数，则有：

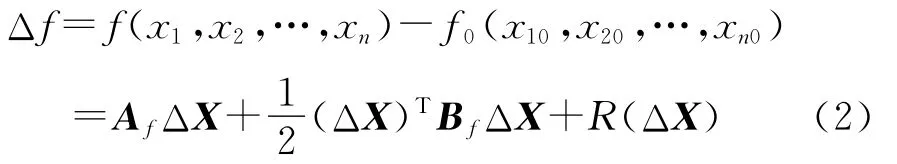
式中，R（ΔX）为参数偏差三阶以上高次项.

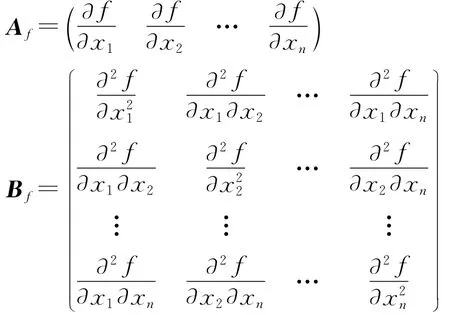
同理，可得到式（1）中的函数ΔF的表达式为

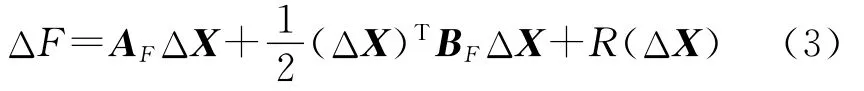
式中，AF，BF表达式与式（2）中Af，Bf类似.将 Δf，ΔF代入式（1），保留二次高阶项，并写成矩阵的形式有：

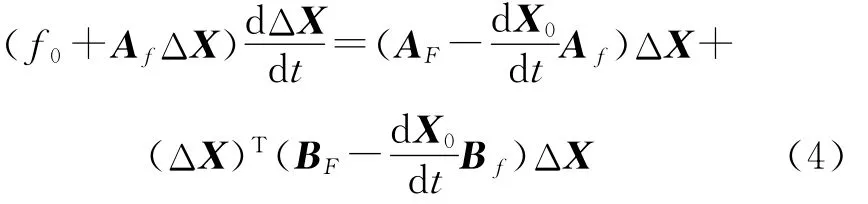
1.2 高超声速飞行器纵向扰动模型

假设推力方向沿发动机轴线，与机身轴线重合；v，γ，θ，q，α，h分别为高超声速飞行器的飞行速度、弹道偏角、俯仰角、飞行器绕本体坐标系Ox1y1z1中的Oz1轴的旋转角速度、迎角以及飞行高度.高超声速飞行器利用式（4）可以建立纵向扰动方程：

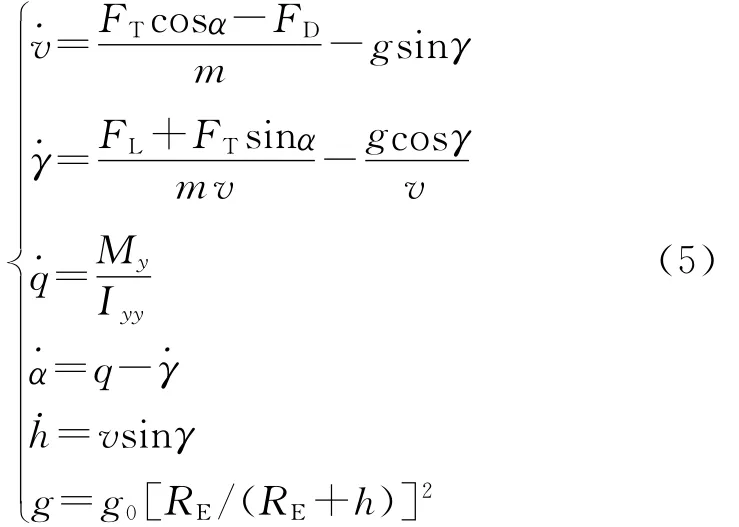
式中，FT，FD，FL，My，Iyy分别为飞行器所受到的推力、阻力、升力、纵向力矩系数和转动惯量.

纵向基准模型可以按照其受力情况在速度坐标系上得到：

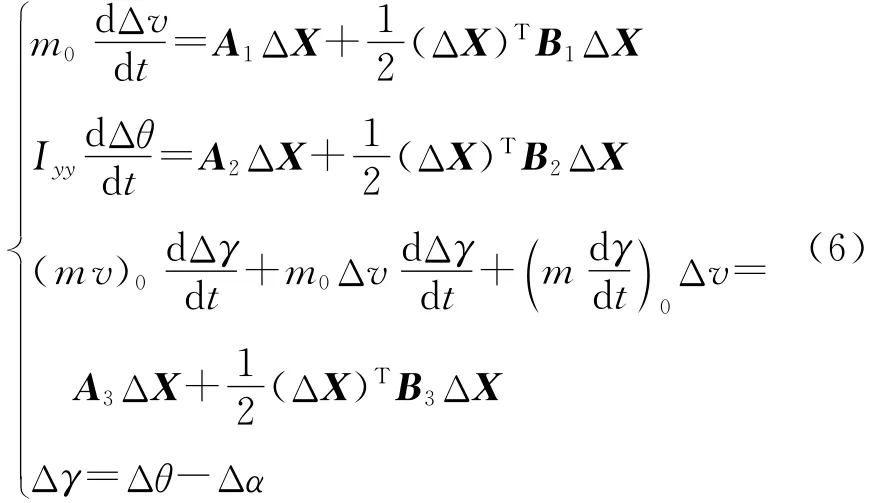
式中，θ为俯仰角；A1，A2，A3为式（2）中Af的展开项，有Af＝（A1A2A3）.

公式的各项含义见参考文献[6].对于式（6）中第3个式子，在一般情况下，要比大得多，两式相比可以忽略不计[4].同时，为了明显列出 Δα的表达式，利用角度几何关系Δα＝Δθ－Δγ，最后整理得到状态变量 ΔX＝（ΔvΔγΔαΔθ）T的矩阵形式：

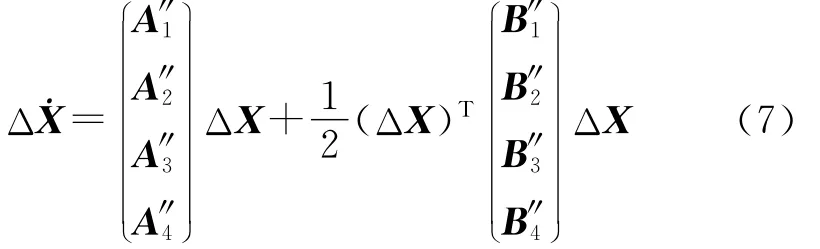
式中，

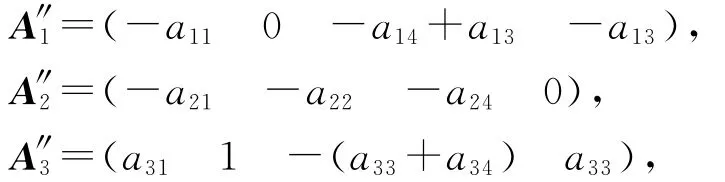
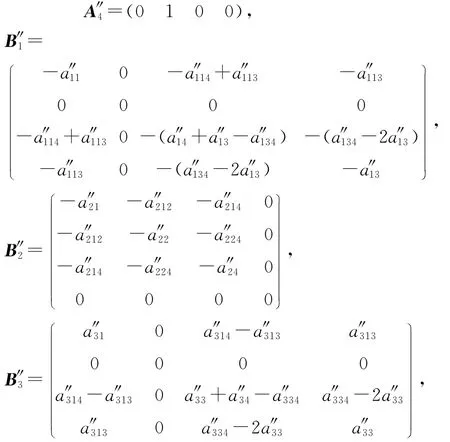
B″4＝O4×4，各系数矩阵中，一次动力系数表达式见参考文献[5]，二次动力系数的表达式见表1.

表1 各二次项动力系数表达式

2 基于常微分方程理论的非线性扰动运动模态动态特性分析方法

针对包含运动参数偏差二次高阶项的非线性扰动运动模型，本文借鉴常微分方程在具有非线性模型特征的生态、电力、生物工程领域动态特性分析问题中的应用，提出高超声速飞行器的非线性扰动运动模态的动态特性分析方法.

2.1 Hopf分支理论

当受到扰动时，动力系统会演变成与之“相邻”的动力系统，这时该动力系统所具有的拓扑结构的性质就有可能发生改变.若系统的拓扑结构不变，则微分方程的结构式是稳定的；否则是不稳定的.如果其结构不稳定，则适当的扰动都会引起系统的拓扑结构发生突然变化，数学上称这种变化为分支.一般来说，含参数λ的n维非线性系统微分方程表示为

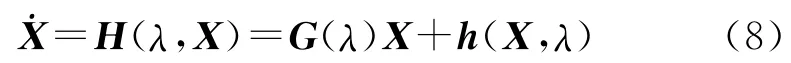
如果参量λ在某一值λc邻近微小变化引起解的性质发生突变，这样的解是结构不稳定的，产生分支现象，此时，λ称为分岔参数.在以参量λc为坐标的轴上，λ＝λc称为分岔点；不引起分岔的点都成为常点.在分岔点的附近，参量值的微小变化足以引起解发生本质的变化（拓扑性质），这样的解是结构不稳定的，可以说分岔意味着方程结构不稳定.当参数λ＜λc时，定点是稳定焦点或者稳定结点；当λ＞λc时，定点变为不稳定定点并出现极限环.极限环是在参数变化时非线性系统解域内存在的孤立闭环.当非线性系统方程的解随自变量的变化无穷趋近极限环时，该极限环成为稳定极限环；当非线性系统的解随自变量的变化远离极限环时，该极限环称为不稳定极限环.

设系统（8）满足：

①h（O，λ）＝0，且（O，0）为系统的非双曲平衡点；

②h（X，λ）在（O，0）的邻域内有L＋2阶连续偏导数（L≥2）；

③G（λ）＝DxH（O，λ）（DxH（O，λ）为非线性方程H（O，λ）的非线性项），在λ＝λc附近有一对复特征值ρ（λ）±iσ（λ），且ρ（λc）＝0，ρ′（λc）≠0，σ（λc）＞0；

④G（λc）的其余特征根都有负实部.

则该系统产生极限环.

2.2 中心流型理论及计算

非线性方程的解结构是随着方程所含的参量变化的.类似于计算气动参数时所做的风洞试验，将飞行器固定，计算风洞气流对于飞行器产生的气动参数；当研究参量对于非线性方程形态的影响时，常将参量值看作一个不动点，研究方程解的形态在此不动点随时间的变化.非线性方程解的变化称为流型，非线性方程在不动点处的解可分为稳定流型、不稳定流型和中心流型.解为中心流型情况可以看做是包含非线性方程解的闭环的环形筒状解域.方程的解随着时间的变化不会发散出该解域也不会收敛于闭环.

中心流型方法的基本思想是，对于高阶非线性方程，在平衡点的邻域内把含有参量的系统展开成相关的幂级数形式，以降低微分方程系统的位数，从而简化微分方程，最终判定微分方程在特定参量下解的稳定性.

在系统（8）平衡点的某个邻域内，给定非奇异线性变化矩阵T，将该系统的雅克比矩阵A＝Dxf（0）化为对角形式，即：

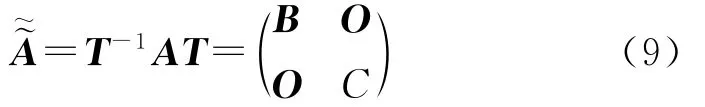
式中，B和C分别为nc×nc和ns×ns矩阵，它们的特征值分别为零实部和负实部.

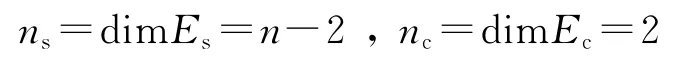
令X＝TY，Y＝（UV）T，U∈Ec，V∈Es；Ec，Es分别为中心子空间和稳定子空间，则有：

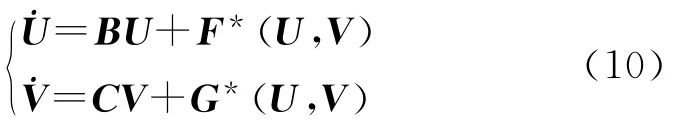
根据参考文献[7]中心流形定理，中心流形在该平衡点邻域内表示为

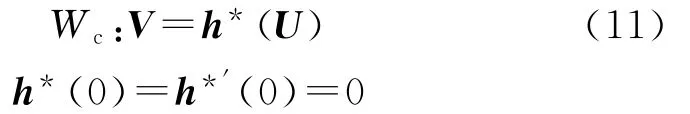
将式（11）代入式（10）第二式，并利用求导的链式法则，有：

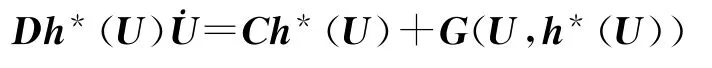
式中，Dxh（U）为非线性方程h（U）的线性项，再利用式（10）第一式，整理后得到h＊（U）的微分方程为

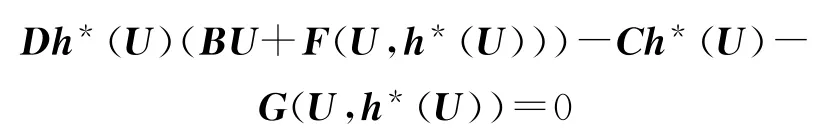
最后得到中心流形上的方程：

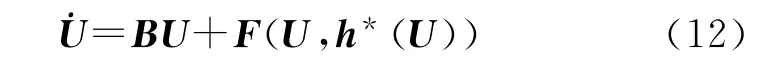
式（12）就是系统（8）在中心流形上的方程，也是该系统降维后的方程，也叫分支方程.

2.3 常微分方程理论在非线性扰动运动特性分析中的应用框图

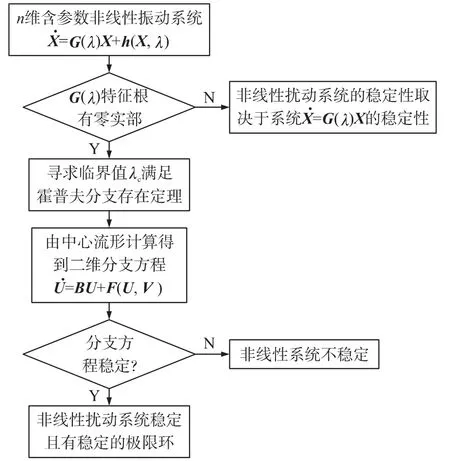
图1 常微分方程分支理论的应用框图

3 仿真分析

针对高超声速飞行器自由扰动运动的稳定性问题，对不同特征点分别采用常规的小扰动的线性化方法和本文所提出的常微分方程理论方法进行结果对比分析.

3.1 仿真条件

分别选取图2中航迹突变点N和等高巡航段中的R为特性点，在不同的静稳定系数下，讨论常规的线性化模型和本文所给出的二阶模型的纵向扰动各模态的动态稳定性.表2为所选定的平衡点参数，表中，H为高度，δ为舵偏角.

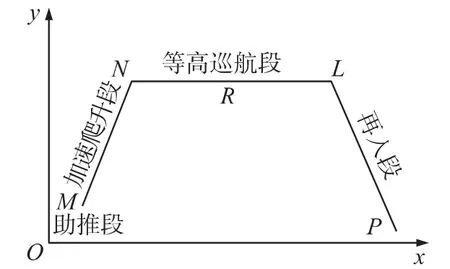
图2 高超声速航迹规划示意图

表2 高超声速飞行器飞行不同特征点的状态参数

3.2 仿真结果

在小动态扰动特性点R处进行自由扰动各模态的动稳定性分析，计算近似线性系统矩阵A的特征值为－4.084 5，0.142 6，－0.001 675±0.013 08i.由常规线性化一阶模型和本文所给的非线性二阶模型得到的纵向扰动运动各参数偏差随时间的变化曲线见图3和图4，2种方法的误差曲线见图5.

在大动态特性点N处进行自由扰动各模的动稳定性分析，计算近似线性系统系数矩阵A的特征值为3.936 14，±0.015 296 200i，－0.009 953 015.在该不动点上，由常规一阶线性化模型得到各参数偏差随时间的变化曲线见图6，可以看出此点处是不稳定的.二阶非线性模型的解出现稳定的极限环如图7所示.线性化模型的飞行参数扰动随时间的变化见图8，图9为在N点邻域的hopf分支图.

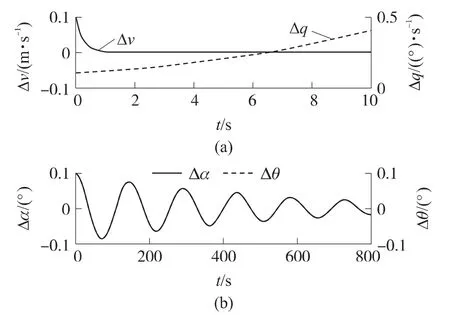
图3 点R处一阶线性化系统下固有扰动性态

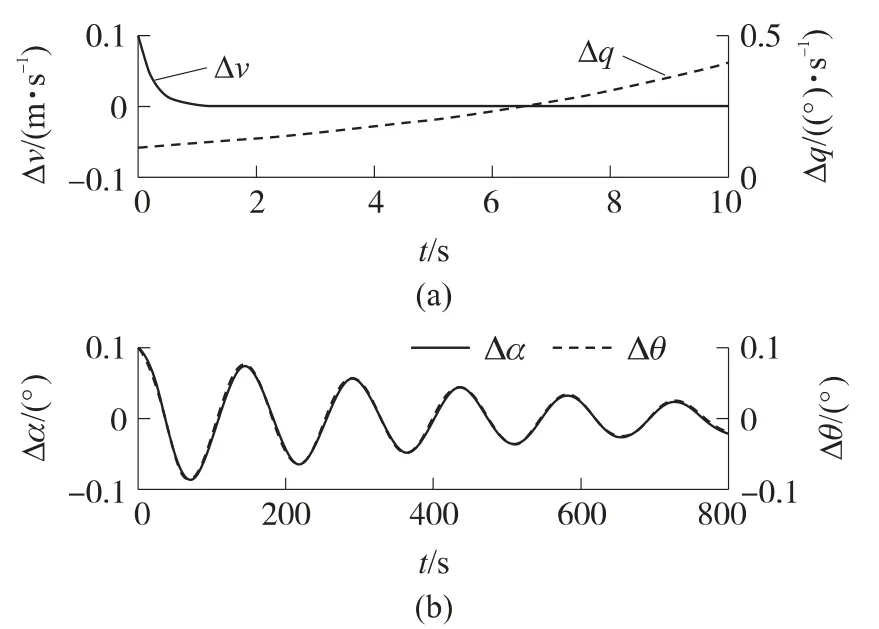
图4 点R处二次高阶项下的固有扰动性态

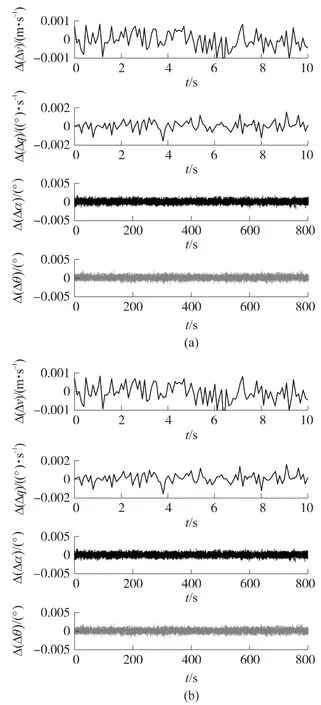
图5 2种处理方法下各模态的误差

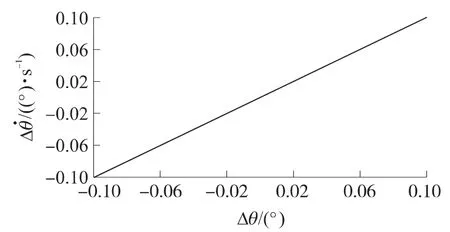
图6 点N处一阶线性化系统下固有扰动性态

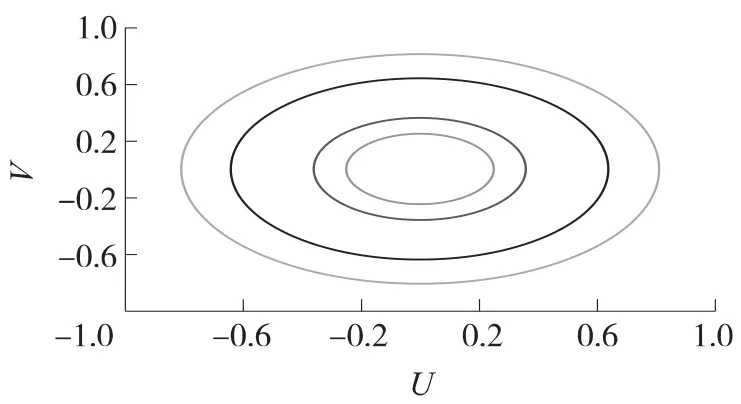
图7 点N处极限环

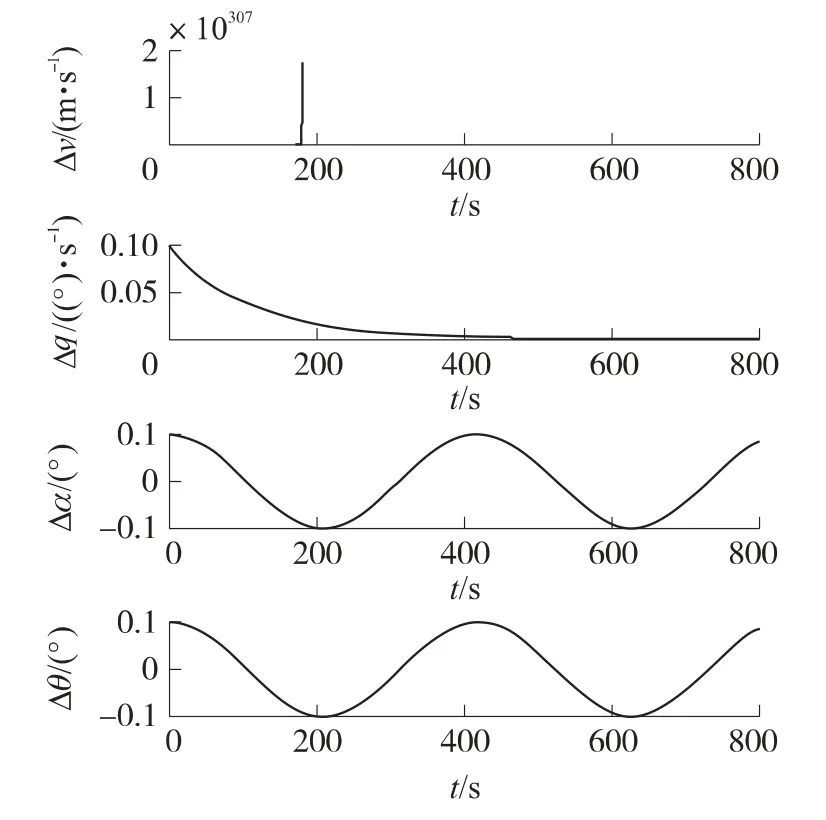
图8 点N处一阶线性化系统扰动量随时间的变化图

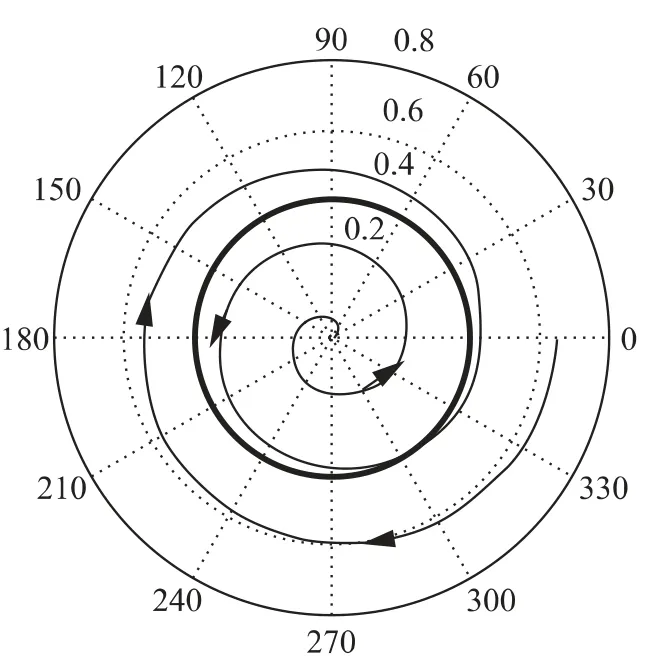
图9 点N处Δθ邻域内的hopf分支

3.3 仿真结果分析

由图3～图5可以看出，在R点处，常规的基于线性化模型的分析方法与保留扰动参数偏差二次项的非线性分析方法的误差在10－3的量级，这说明在小动态环境下，采用常规的基于线性化的稳定性分析方法可以对飞行器稳定性进行准确的分析；由特征根的性质知高超声速飞行器纵向模型的短周期模态是不稳定的；长周期模态是接近中立稳定的.

对比图6、图7和图8、图9可以看出，在大动态环境下，由常规近似线性系统分析方法给出了高超声速飞行器不稳定的结论；而由本文提出的基于微分方程理论的稳定性分析方法得到了稳定的hopf分支，这足以说明，在高动态环境下由常规的线性化建模方法建立的模型已经不能准确地反映扰动运动的特性，必须建立含有参数偏差高次项的非线性模型.

4 结束语

本文首先给出了保留二阶高次项下非线性扰动运动的建模方法；讨论了在不同特性点下，高超声速飞行器纵向扰动系统在平衡点的稳定性；通过对已有的小扰动线性化处理方法的结果进行对比，得到以下结论：

①在小动态环境下，本文所给出的方法与常规的小扰动线性化处理方法结果一致，因此采用小扰动线性化处理方法进行动态特性分析是可行的；

②在大动态环境下，由常规的线性化建模方法建立的模型不能准确地反映扰动运动的特性，必须建立含有参数偏差高次项的非线性模型，本文给出了含有参数偏差二阶高次项的非线性扰动建模方法；

③在建立非线性扰动模型的基础上，给出了基于常微分方程理论的非线性扰动运动动态特性分析方法.

本文的研究结果虽然可以为诸如高超声速这类具有高动态、大范围机动、复杂的非线性动力学特性的飞行器的动态特性分析提供一定参考，但这仅仅只是一个初步的探讨和起步，还有很多值得进一步深入研究的问题，例如非线性扰动运动的稳定域问题，非线性强迫扰动的分析问题及在分支情况下其混沌的控制问题等.

[1]CHAVEZ F R，SCHMIDT D K.Dynamics of hypersonic flight vehicles exhibiting significant aeroelastic and aeroproplusive interactions，AIAA93－3763[R].1993.

[2]CHAVEZ F R，SCHMIDT D K.Analytical aeropropulsive/aeroelastic hypersonic－vehicle model with dynamic analysis[J].Journal of GCD，1994，17（6）：1 308－1 319.

[3]TARPLEY C.The optimization of engine－integrated hypersonic waveriders with steady state flight and static margin constraints[D].USA：University of Maryland，1995.

[4]李新国，方群.有翼导弹飞行动力学[M].西安：西北工业大出版，2005.

[5]VADDIL S S，SENGUPTA P.Controller design for hypersonic vehicles accommodating non－linear state and control constraints，AIAA 2009－6286[R].2009.

[6]BOLENDER M A，DOMAN D B.A non－linear model for the longitudinal dynamics of a hypersonic air－breathing vehicle，AIAA 2005－6255[R].2005.

[7]ANDERSON D.Modern compressible flow[M].3rd ed.New York：McGraw Hill Higher Education，2002.