肋环型索穹顶结构的几何法施工及工程应用

张 成，吴 慧，高博青，王昌洪

1)浙江大学建筑工程学院，杭州310058;2)浙江财经学院工商管理学院，杭州310018;3)晟元集团有限公司，浙江金华321000

索穹顶结构作为一种张力集成体系，最大限度地利用了材料和截面的特性，可以用尽量少的钢材建造大跨度建筑. 通过理论分析［1-2］和试验研究［3-4］，各种形式的索穹顶结构的找形找力分析［5-6］、预应力优化［7-8］、其静动力性能［9］及局部构件失效时的受力性能［10-11］已较为明确，并不断有新的结构形式提出［12-13］. 但索穹顶结构能否实现从松弛的零状态到设计的自平衡预应力状态，与结构的实际施工张拉过程密切相关，须选择合理、有效的施工方法.

在施工过程中，索穹顶结构的索杆体系发生大位移和大转角，并伴随着刚体运动、机构运动和弹性变形，使施工过程的跟踪和精度控制都较困难.由于技术保密等原因，国外对索穹顶的施工过程只有简单描述［14-16］. 国内有学者根据非线性有限元［17］或动力松弛法［18］，将施工成形问题转化为形态分析，目前研究较多的施工方法主要包括调节压杆长度［18］及张拉斜索、脊索或环索［19］等，而张拉调整可以分批分次进行或一次张拉到位［20-21］. 以上施工方法通过算例或模型试验证实可行，但计算复杂，或者实施过程不够明确. 本研究针对索穹顶结构张拉难于控制、安装技术要求高的问题，提出一种只需张拉端部斜索的肋环型索穹顶几何法施工成形方法，根据竖压杆、脊索和斜索之间的几何关系，计算在安装过程中竖压杆的临时安装标高.

1 几何法施工原理

用几何法安装肋环型索穹顶结构，是利用拉索节点之间的距离小于其原长，安装时可不用张拉设备的原理，通过几何方法给出肋环型索穹顶在安装过程中满足这一条件的竖压杆安装标高，从而实现只需张拉端部斜拉索即可使索穹顶结构成形.

1.1 安装张拉顺序

图1(a)为典型的肋环形索穹顶结构剖面图，脊索上节点从结构中心至环梁分别为S1、S2、…、Sn，竖杆下节点分别编号为X1、X2、…、X(n-1). 其安装张拉顺序为:①将脊索置于地面上，在其上安装上节点，将各个竖杆上端分别与脊索连接，然后将脊索连于外压环梁节点Sn～Sn之间，如图1(b)，其中实线为安装完成的结构，虚线为安装完毕时结构的形状，余同. ②安装脚手架，顶升脊索中心节点S1至设计最终标高位置，用斜索连接脊索节点S2和竖杆下节点X1，如图1(c). ③顶升竖杆下节点X2到达设计的临时标高位置X2，用斜索连接脊索节点S3和竖杆下节点X2，同时安装第1 圈环索. 根据设计计算，此时节点X2与节点S3之间的距离小于斜索原长;环索节点由于处于最终位置的内侧，其间距离小于原长，因此拉索均处于松弛状态，以上安装不需张拉. 对其余各环从内到外重复以上步骤，直到整个结构各竖杆和中心环均达到设计的临时位置为止，如图1(d). ④张拉端部斜索，使整体结构到达到如图1(a)的最终设计形状.

图1 安装张拉顺序Fig.1 Tensioning schemes

1.2 竖杆临时安装标高的确定

取图1(a)中肋环形索穹顶结构部分作为计算单元，如图2 所示，其中实线为结构最终形状，虚线为安装时的临时位置. 设在节点i 处的竖杆长度为hi，节点i 与节点i +1 之间的脊索长度为ai，并假设脊索和压杆在自重作用下的伸缩量与原长相比可忽略不计，即计算时脊索和竖压杆可取其原长ai、hi. 为能不用张拉即可安装斜索，施工过程中斜索两端节点间距离b'i 应小于斜索原长(含节点几何尺寸)，本研究取b'i = 0.95bi;而由于节点i+1 的位置在结构初始态的内侧，安装节点i+1 下方对应的环索时可不用张拉. 根据竖压杆、脊索和斜索之间的几何关系，

节点i +1 相对其最终设计标高应下降的距离Δi+1可表示为

代入不同的ai、hi和αi，可求得i 节点应下降的垂直距离

由式(1)～(4)，可求得脊索各节点的施工安装临时标高，进而可得各竖压杆安装标高.

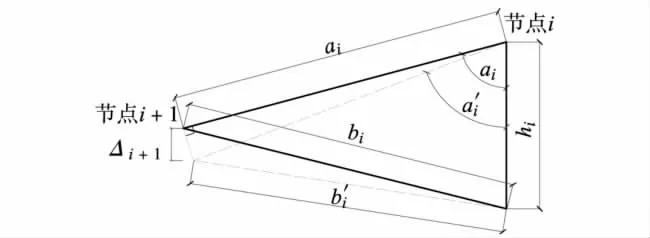
图2 计算单元Fig.2 Typical calculation unit

表1 一圈环索的索穹顶结构节点下降高度与跨度之比( /l )Table1 /l of the cable domes with only one ring of hoop cable

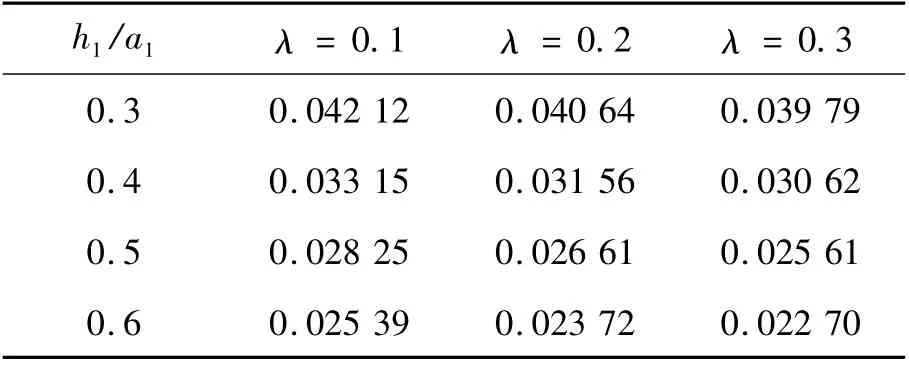
表1 一圈环索的索穹顶结构节点下降高度与跨度之比( /l )Table1 /l of the cable domes with only one ring of hoop cable

h1/a1λ = 0.1λ = 0.2λ = 0.3 0.30.042 120.040 640.039 79 0.40.033 150.031 560.030 62 0.50.028 250.026 610.025 61 0.60.025 390.023 720.022 70

2 应用实例

2.1 结构总体设计

图3 结构总体设计图Fig.3 General design of the cable dome

某标准厂房中庭采用索穹顶结构，其总体设计见图3. 平面为一双轴对称椭圆形，如图3(a)，长轴20 m，短轴18 m，矢高2.25 m. 结构径向有3类共4 榀，如图3(b)～(d)，环向共设2 圈环索，脊索固定于周边环梁. 环梁采用350 mm ×250 mm×10 mm ×16 mm 的焊接工字型梁，拉索为Φ26 ～36 mm 钢绳索，压杆采用Φ60 mm×3.5 mm 无缝钢管. 设计恒荷载0.2 kN/m2，活荷载0.55 kN/m2，风荷载吸力0.35 kN/m2，压力0.25 kN/m2. 表2给出拉索的预应力p，以及在风压力和吸力2 种工况下的设计内力值Nd与Nu. 为便于连接，脊索和斜索一端索头为螺杆，另一端为单插板，环索两端均为U 插板.

根据式(1)～ (4)，计算其脊索各节点安装时下降高度，标于图3(a).

表2 拉索的内力Table 2 Internal forces of cableskN

2.2 节点设计

索与索，及索与杆的连接是索穹顶结构施工中的关键之一，对于索穹顶结构，目前尚未形成统一的节点构造体系，考虑传力简捷明确和制作安装方便两方面要求［22］，各类节点(见图3)设计如图4.

①拉索与受压环梁连接节点(BJD1 ～BJD3)

索穹顶结构的索杆体系自身并不能形成应力回路，需要和受压环梁连接组成整体自平衡体系. 设计斜索端头的单插板通过销钉与焊接于环梁的耳板连接，斜索穿过环梁利用螺栓锚固在节点板上，如图4(a)所示.

②脊索、斜索与压杆的连接节点 (SJD1 ～SJD6)

设计脊索在节点间并不断开，整根拉索是贯通的. 为防止节点沿脊索滑动，在上下盖板开槽将脊索压牢;斜索和压杆分别通过端头的单插板利用销钉与节点板连接，如图4(b)所示.

图4 索穹顶节点设计Fig.4 Design of the joints

③斜索、环索与压杆连接节点 (XJD1 ～XJD6)

环索端头的U 插板利用销钉与节点底板连接;斜索和压杆分别通过单插板利用销钉与节点竖板连接，如图4(c)所示.

④中心节点

中心节点处有8 根脊索 (SZJD)或斜索(XZJD)交汇，设计箱型节点，拉索穿过节点板用螺栓锚固，而压杆则直接焊接于节点板，如图4(d)所示.

2.3 操作要点与关键技术

由于索穹顶结构对构件尺寸比较敏感，安装前应检查确定索穹顶所有构件以及设置在受压环梁上锚固节点的位置、尺寸是否符合设计要求. 将构件编号，以免错装. 如受压环梁上的锚固节点存在较大误差，应对上弦脊索长度或受压环梁上的锚固节点本身进行调整.

安装时，首先将脊索通过节点串联起来，悬挂于受压环梁上. 然后在竖压杆的下方搭设脚手架，脚手架的高度应能使竖压杆的安装高度与本研究提供的标高一致，并且使工人能在脚手架上进行操作. 最后从索穹顶中心开始，逐圈安装竖压杆、环索、斜拉索;当拉索较长时，应有临时支撑防止拉索过度下垂安装不上，一般情况可借助手拉葫芦进行安装. 每安装一圈后，应调整竖杆的标高到指定的位置. 在最后安装端部斜拉索时，应以对称张拉为宜. 如果出现拉索长度不够而不能穿过受压环梁上锚固节点的情况，可通过两个途径解决:一是加长端部斜拉索500 ～1 000 mm，同时，用穿心形千斤顶;二是加长拉杆，将端部斜拉索拉至设计位置，然后锚固于受压环梁上.

按照几何法现已完成2 座索穹顶的安装，取得较好效果. 该安装方法已申请国家专利和工法.

结 语

索穹顶结构张拉难于控制，安装技术要求高，国内尚未有涉及索穹顶的施工工法. 本文根据竖压杆、脊索和斜索之间的几何关系，提出一种只需张拉端部斜索的肋环型索穹顶结构施工成形方案. 采用几何法施工方法只需张拉斜索，索穹顶结构会自动成形，不需要大规模调整拉索的预应力，甚至当控制好端部斜拉索的张拉几何位置和张拉力时，不需要调整任何拉索的预应力，从而降低了施工技术要求，脚手架只需在竖压杆下部搭设，工程造价经济. 按照几何法安装了国内第一座索穹顶结构，并设计了索杆连接的各种节点，为索穹顶的安装积累了经验，提高了大跨度结构的施工水平，使这种原施工技术要求极高的结构有可能得到普遍推广.

/References:

［1］YUAN Xing-fei，DONG Shi-lin. Application of integrity feasible prestressing to tensegrity cable domes ［J］. China Civil Engineering Journal，2001，34(2):33-37.(in Chinese)袁行飞，董石麟. 索穹顶结构整体可行预应力概念及其应用［J］. 土木工程学报，2001，34(2):33-37.

［2］DONG Shi-lin，YUAN Xing-fei. A simplified calculation method for initial prestress distribution of sunflower-patterned cable domes［J］. Journal of Building Structures，2004，25(6):9-14. (in Chinese)董石麟，袁行飞. 葵花型索穹顶初始预应力分布的简捷计算法［J］. 建筑结构学报，2004，25(6):9-14.

［3］ZHENG Jun-hua，LUO Yao-zhi，DONG Shi-lin，et al.Model experimental research on rectangular cable dome［J］. Journal of Building Structures，2008，29(2):25-31.(in Chinese)郑君华，罗尧治，董石麟，等. 矩形平面索穹顶结构的模型试验研究［J］. 建筑结构学报，2008，29(2):25-31.

［4］CHEN Lian-meng，DONG Sh-lin，YUAN Xing-fei. Experimental study of Kiewitt dome model［J］. Journal of Zhejiang University Engineering Science，2008，42(2):364-368.(in Chinese)陈联盟，董石麟，袁行飞. Kiewitt 型索穹顶结构模型试验研究［J］. 浙江大学学报工学版，2008，42(2):364-368.

［5］Wang Z H，Yuan X F，Dong S L. Simple approach for force finding analysis of circular Geiger domes with consideration of self-weight ［J］. Journal of Constructional Steel Research，2010，66(2):317-322.

［6］Xi Y，Xi Z，Qin W H. Form-finding of cable domes by simplified force density method ［J］. Proceedings of the Institution of Civil Engineers-Structures and Buildings.2011，164(3):181-195.

［7］Yuan X F，Wang Z H，Dong S L. Simplified techniques for prestress design and load analysis of geiger domes［J］. Advanced Science Letters，2011，4(8/10):3256-3260.

［8］Fang H Q，Zhou C T，Yang F. Research on Analysis Method and Distributing Principle of the Optimal Prestress in Sunflower-patterned Cable Dome ［M］. Stafa-Zurich(Swiss):Trans Tech Publications Ltd，2011:163-167，740-744.

［9］Chen L M，Dong S L. Dynamical Characteristics Research on Cable Dome ［M］. Stafa-Zurich:Trans Tech Publications Ltd，2011:163-167，3882-3886.

［10］HE Jian，YUAN Xing-fei，JIN Bo. Analysis of cable domes with rupture of local cable ［J］. Journal of Vibration and Shock，2010，29(11):13-16.(in Chinese)何 键，袁行飞，金 波. 索穹顶结构局部断索分析［J］. 振动与冲击，2010，29(11):13-16.

［11］XU Guo-jie，ZHUO Xin，SHOU Quan-gen. Structural performance of TH-Levy cable dome when local component failure ［J］. Journal of Zhejiang University Engineering Science，2011，45(7):1281-1287.(in Chinese)许国杰，卓 新，寿全根. TH-Levy 型索穹顶局部构件失效时的受力性能［J］. 浙江大学学报工学版，2011，45(7):1281-1287.

［12］Yuan X F，Chen L M，Dong S L. Prestress design of cable domes with new forms ［J］. International Journal of Solids and Structures，2007，44(9):2773-2782.

［13］YUAN Xing-fei，DONG Shi-lin. New forms and initial prestress calculation of cable domes ［J］. Engineering Mechanics，2005，22(2):22-26.(in Chinese)袁行飞，董石麟. 索穹顶结构的新形式及其初始预应力确定［J］. 工程力学，2005，22(2):22-26.

［14］Geiger D H，Stenfaniuk A，Chen D. The design and construction of two cable domes for the Korean Olympics［C］// Proceedings of the IASS-ASCE International Symposium on Shells，Membranes and Space Frames. Osaka(Japan):Elsevier，1986:265-272.

［15］Levy M P. Georgia dome and beyond:achieving lightweight-longspan structures ［C］// Proceedings of the IASS-ASCE International Symposium 1994 on Spatial，Lattice and Tension Structures. Atlanta (America):ASCE，1994:560-562.

［16］Terry，Wesley R. Georgia dome cable roof construction techniques ［C］// Proceedings of the IASS-ASCE International Symposium 1994 on Spatial Lattice and Tension Structures. Atlanta (America):ASCE，1994:563-572.

［17］SHEN Zu-yan，ZHANG Lin-xin. Simulation of erection procedures of cable domes based on nonlinear FEM ［J］.Computational Mechanics，2002，19(4):414-419. (in Chinese)沈祖炎，张立新. 基于非线性有限元的索穹顶施工模拟分析［J］. 计算力学学报，2002，19(4):414-419.

［18］CHEN Lian-meng，DONG Shi-lin，YUAN Xing-fei. Theoretical and experimental study on the construction of cable domes ［J］. China Civil Engineering Journal，2006，39(11):33-36，113. (in Chinese)陈联盟，董石麟，袁行飞. 索穹顶结构施工成形理论分析和试验研究［J］. 土木工程学报，2006，39(11):33-36，113.

［19］ZHENG Jun-hua，DONG Shi-lin，ZHAN Wei-dong. Experimental research on construction process of Levy type cable domes ［J］. Journal of Building Structures，2006，27(1):112-116.(in Chinese)郑君华，董石麟，詹伟东. 葵花型索穹顶结构的多种施工张拉方法及其试验研究［J］. 建筑结构学报，2006，27(1):112-116.

［20］CHEN Lian-meng，DONG Shi-lin，YUAN Xing-fei. Theoretical analysis of construction procedures of cable-domes［J］. Engineering Mechanics，2008，25(4):134-139.(in Chinese)陈联盟，董石麟，袁行飞. 索穹顶结构施工成形理论分析［J］. 工程力学，2008，25(4):134-139.

［21］YUAN Xing-fei，DONG Shi-lin. Inverse analysis of construction process of cable dome ［J］. Journal of Building Structures，2001，22(2):75-79，96.(in Chinese)袁行飞，董石麟. 索穹顶结构施工控制反分析［J］.建筑结构学报，2001，22(2):75-79，96.

［22］CHENG Rui，HE Jing-yun，HUANG Zong-ming，et al.Study on tension and block shear behavior of bolted single angle-gusset plates ［J］. Journal of Shenzhen University Science and Engineering，2009，26(4):382-388. (in Chinese)程 睿，何井运，黄宗明，等. 单角钢螺栓连接节点板拉剪性能研究［J］. 深圳大学学报理工版，2009，26(4):382-388.