对《一道解析几何题的多种解法》的补充
2012-12-23 03:51谢瀛慧
武汉商学院学报 2012年2期
谢瀛慧
(武汉商业服务学院,湖北 武汉 430056)
《数学通报》2006 年第4 期薛孝乐的《一道解析几何题的多种解法》一文,用不等式、导数、行列式、向量、定积分等知识求解了这样一道解几问题:“已知直线L;Y=4X 和点R(6,4),在L 上求一点Q使直线RQ 与L 及X 轴在第一象限内所围成的三角形面积最小(见图)”。

文中解法三有误,其余几种解法较为新颖,读后觉得此文求解过程不够简捷,使学生难以接受。本文对原文解法三给予更正以及再给出几种解法,作为原文的补充。
一、更正错误
现将原文解法三抄录如下:
解法三 设点Q(X0,4X0),(X0>1)直线QR 交X轴于P(a,0),则
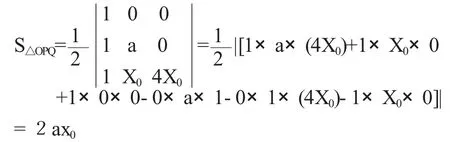
以上求解过程,两步都是错的。更正如下;
第一步应为

二、解法补充

下同原文解法1。
解法2,设所求直线PQ 的方程为;所以点Q 的坐标为:



要使k 有实数解,则△=(4S-96)2-4(72-S)×32=16(S2-40S)≥0,于是,S≥40
即S 最小等于40,当S=40,代入(3)得,k2+2k+1=0
∴k=-1,代入(2)得Q 的坐标为(2,8),
解法3 由解法2 已知△OPQ 三顶点的坐标为

下同解法2
解法4 定理(文[1])若△ABC 的三边由方程,aiX+biY+ci=0,(i=1,2,3)给出,则它的面积

下同解法2。
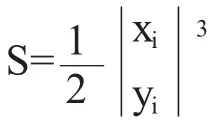

[1]贾士代.三角形的一个面积公式[J].数学教学研究.1988(6).
[2]伍启期.二行n 列式的理论及其应用[J].数学通报.1981(5).
猜你喜欢
轻工标准与质量(2022年4期)2022-08-25
轻工标准与质量(2022年3期)2022-06-29
轻工标准与质量(2022年1期)2022-03-07
轻工标准与质量(2021年6期)2021-12-31
教师·下(2017年10期)2017-12-10
读写算·小学低年级(2017年1期)2017-02-06
Water Science and Engineering(2014年1期)2014-03-06
云南教育·小学教师(2012年10期)2012-11-22
数学大世界·小学低年级辅导版(2010年4期)2010-03-25

