基于高开关频率精确模型的峰值电流型BUCK 电源的补偿设计*

阚明建，徐 申，孙伟锋

(东南大学国家专用集成电路系统工程技术研究中心，南京210096)

峰值电流控制模式的BUCK 电源，由于其快速响应、电路简单、易于集成的特性，被广泛应用于电源管理芯片中。为了增加系统的瞬态响应和降低电源元器件的体积，节省成本，电源的开关频率也在逐渐增加，已经达到MHz 以上。为了降低功耗，给SOC 和内存供电的电源管理芯片需要输出电压可调的功能。在调节输出电压的过程中，为了防止输出电压突变时涌入大量电流对系统造成影响，采用参考电压Vref的DAC 技术［1］。但是采用此技术调节输出电压，如图1 所示，当Vref阶跃变化时，如果电源的环路补偿不合适，会造成输出电压的过冲和振荡，引入电磁干扰，对电源的稳定性造成影响。为了克服输出电压的过冲和优化输出电压的瞬态响应，需要对峰值电流模式的BUCK 电源进行小信号模型分析，并进行频率补偿设计。

文献［2－8］，对峰值电流模式的BUCK 电源的小信号模型进行了一定的研究，但是没有考虑开关管的导通电阻和寄生参数，因此在低压大电流的模型中会造成误差。针对电源环路的频率补偿模块，文献［7－8］设计了消除环路主极点来增加系统环路单位增益带宽的方法，但是主极点会随着输出电阻和输出电压的变化而变化，给频率补偿带来了困难。

本篇论文，针对上述问题，建立了峰值电流BUCK 电源的精确小信号模型，设计了一个新颖的补偿模块。在第2 部分中，推导了带有开关管导通损耗和寄生参数的峰值电流的BUCK 小信号模型，并进行了频率补偿设计。在此模型基础上，第3 部分分析了输出电压Vo对参考电压Vref的传递函数的频率响应，得出了补偿模块的最佳增益，使得输出电压的瞬态响应既快速又没有过冲和振荡。第4 部分利用Spice 电路仿真，对精确的小信号模型和补偿模块最佳增益进行了仿真验证。

1 精确小信号模型推导

峰值电流模式BUCK 电源的系统框图如图1 所示，输出电感L、电容C 的寄生电阻分别为rL、rc，开关管S1和同步整流管S2的导通电阻分别为r1、r2，电流采样电阻为Rs。设开关的占空比为d(t)，电感电流为iL(t)，开关周期为T。在一个周期T 内，开关管PMOS 和NMOS 的连结点电压V2(t)为:

图1 利用DAC 技术的峰值电流BUCK 电源的系统框图

根据开关元件平均模型法，对V2(t)进行线性化，并进行小信号剥离，得到:

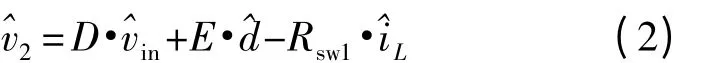
其中E=Vin－IL·(r1－r2)，Rsw1=r1D+r2·(1－D)，

把Rsw=Rsw1+rL变换后可得BUCK 拓扑结构的小信号模型，如图2 所示。

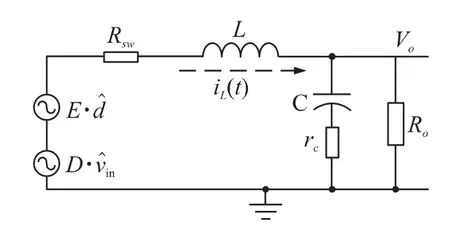
图2 BUCK 的功率级小信号模型

峰值电流控制环路如图1 所示，包含频率补偿模块Tc，电流采样和占空比调制模块。频率补偿模块Tc如图3 所示，OP 是运算放大器，R2和R4是运算放大器输入端的电阻。R1，R3和C1，C3是频率补偿电阻和电容，满足C1=C3，R1=R3，R2=R4。因此:

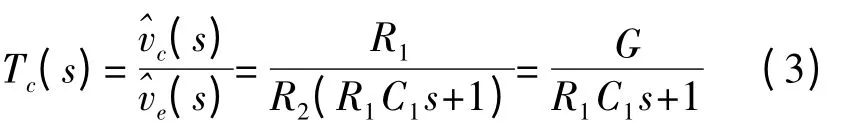
其中，ve=Vref－V0，G=R1/R2是补偿模块Tc的直流增益。

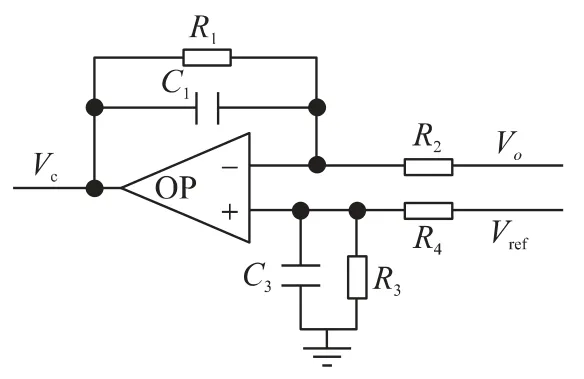
图3 频率补偿模块Tc

［9－10］，可以得到峰值电流环路的小信号模型。把功率级模型和控制环路模型结合起来，即得到峰值电流型的BUCK 电压源的完整小信号模型，如图4 所示。

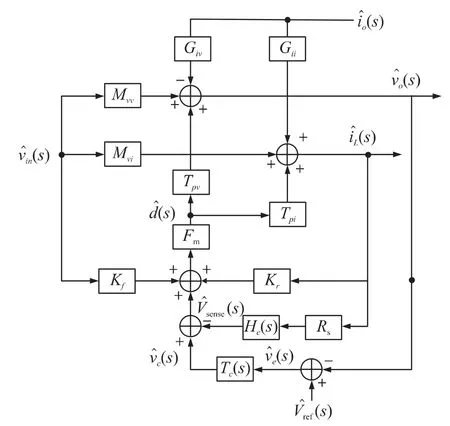
图4 峰值电流BUCK 电源的系统模型

功率模型中的传递函数Mvv、Mvi，Giv、Gii，Tpv、Tpi，是输入电压Vin、占空比d、负载电流Io分别对输出电压、电感电流的影响。控制模型中的Fm是调制系数，He是电流采样效应引入的函数，Rs为电感电流的采样电阻，Kf和Kr分别是输入电压Vin和输出电压对占空比d 的影响，Tc是频率补偿模块，用于补偿电压环路。M1、M2、Ma为电流检测的电流上升斜率、下降斜率、电流的补偿斜率。其表达式如下所示:

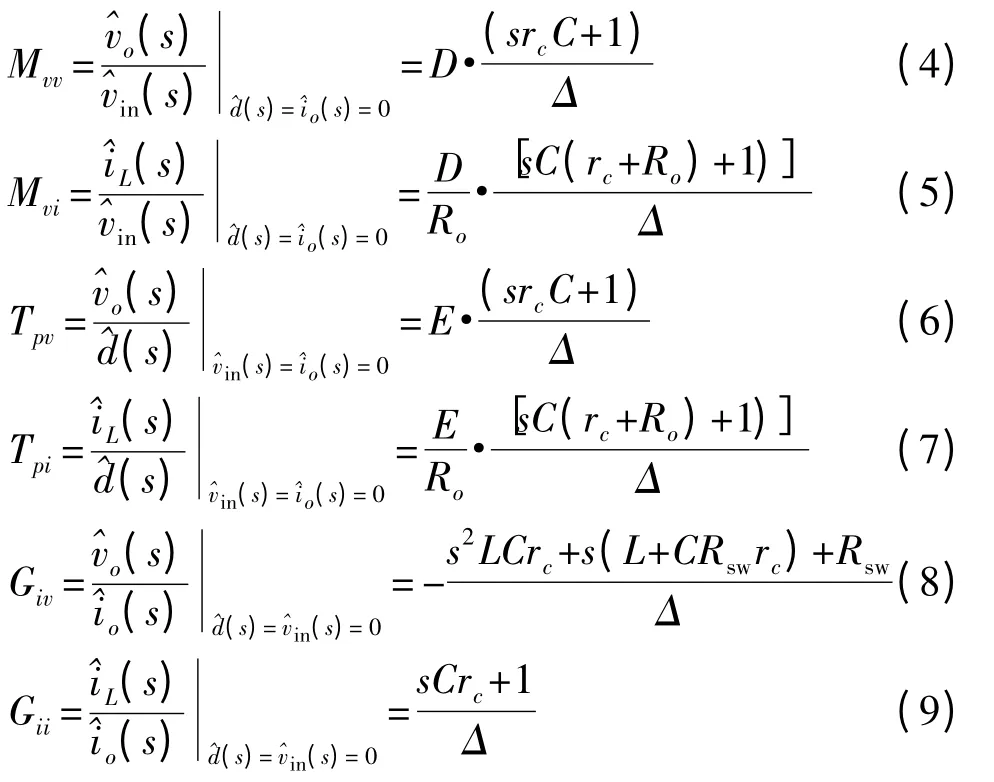
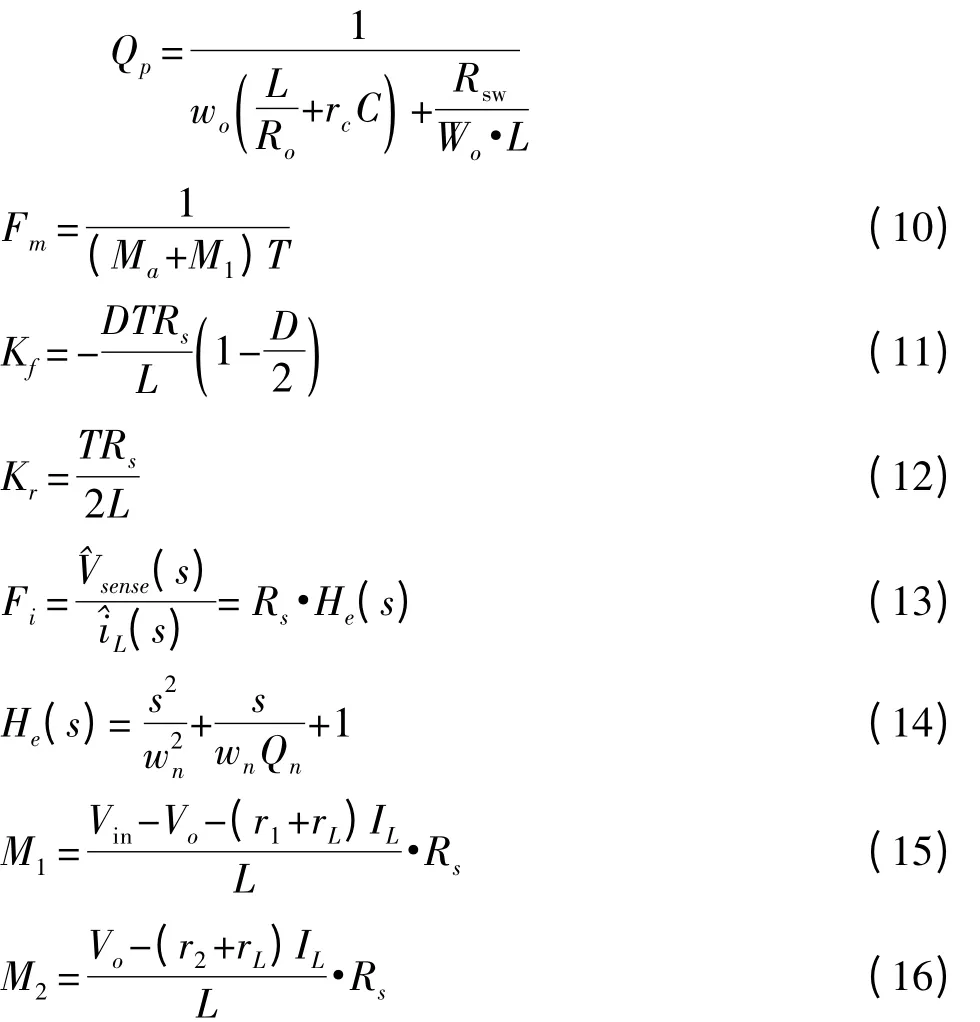
2 系统分析与补偿模块优化

根据图4 和梅逊公式，可以得出电流环和电压环闭环后，输出电压相对于参考电压的传递函数Hr的表达式:

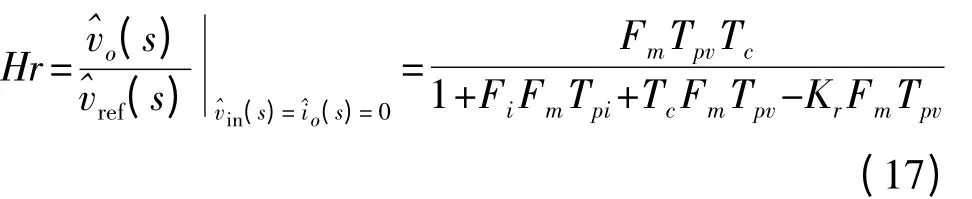
为了分析传递函数Hr 的频率特性，首先分析电流环闭合，不包含频率补偿模块的电压环开环传递函数Ac，表达式:

把式(4)～式(16)代入上式得:

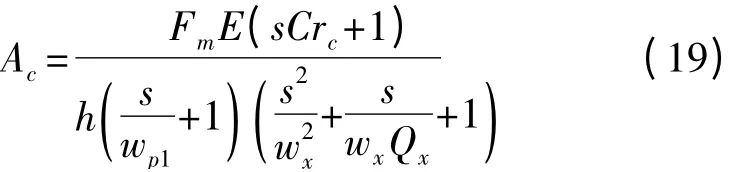
从式(19)可以得出，Ac存在一个主极点wp1，一个零点wz1，和两个共轭极点，约在fs/2 处。当电压环包含频率补偿模块Tc后，电压环的环路增益为式:

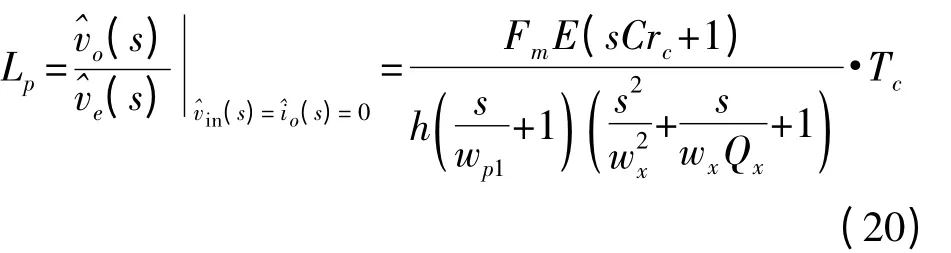
在文献［7－8］中，为了使总体电压环路Lp的带宽足够大，采用消去主极点wp1的办法，但是主极点会随着输出电阻Ro和输出电压Vo的变化而变化，给频率补偿带来了困难。但零点是一个定值，不会随着输出电阻Ro和输出电压Vo变化。且当开关频率达到MHz 以上时，滤波电容的寄生电阻引入的零点影响会很大。因此提出一个新颖的频率补偿模块，如图3 所示。仅增加一个极点，消除输出电容寄生电阻引入的零点。满足C1·R1=C·rc来消除滤波电容寄生电阻引入的零点wz1。经过频率补偿后电压环路Lp的频率响应如图5 所示，从图5 可以看出，其环路Lp可以很好的满足系统稳定性判据［11］。

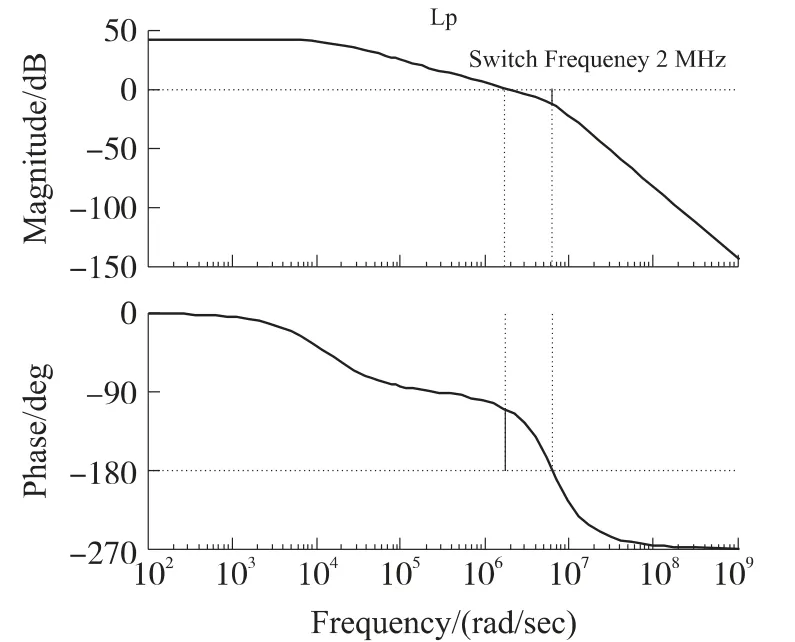
图5 经过补偿后电压环Lp 的频率响应

虽然系统可以稳定，且系统的单位增益带宽越宽，输出电压的瞬态响应也越快。但是输出电压会出现过冲和振荡，当参考电压发生阶跃变化时，如图6 虚线所示。因此当采用DAC 技术调节输出电压时，输出电压的波形会出现大量毛刺和波动。如果输出电压对于参考电压的瞬态响应没有过冲，就不会出现毛刺和波动，得到一个平滑的输出电压波形。

图6 Vref阶跃变化时输出电压的瞬态响应

根据式(17)，我们可以得出

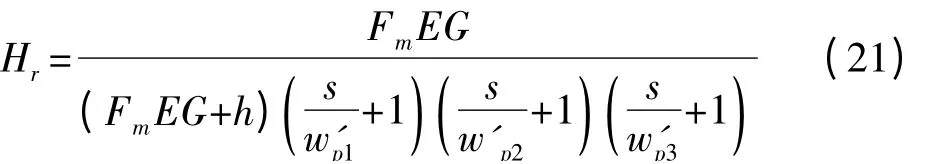
传递函数Hr有三个极点，一个主极点wp1，一对共轭极点wp2和wp3。如果主极点wp1远小于共轭极点wp2和wp3时，其阶跃响应不会出现过冲，但是其瞬态响应较慢。如果共轭极点远小于主极点wp1，共轭极点会引起谐振波峰使得Hr的幅值大于1，引入过冲和振荡。根据文献［12］的理论，即如果不存在零点，且第一个极点和共轭极点的实数值相等时，此传递函数Hr的阶跃响应单调增加。因此最佳的选择是:主极点wp1等于共轭极点wp2和wp3的实数部分，因此可以得到频率补偿模块最佳的直流增益G，使得Hr的瞬态响应既快速又没有过冲。

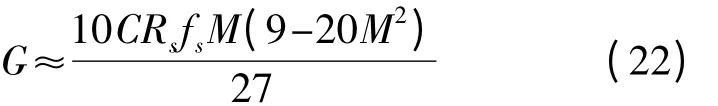
其中，M=mcD'－0.5

当频率补偿模块采用最佳直流增益时，其输出电压阶跃响应的波形没有过冲，且反应较快，如图6实线所示。

3 模型验证

在上文，我们已经得到开关电源的精确小信号模型，设计了针对高开关频率电源的补偿模块Tc，分析得出此模块最佳的直流增益，使得输出电压相对于参考电压的瞬态响应，既快速又没有电压过冲和振荡。为了验证上述推导的正确性，在Spice 仿真中搭建的电路图如图7 所示，开关管S1和S2的导通电阻分别为0. 19 Ω 和0. 16 Ω，系统的参数如下:

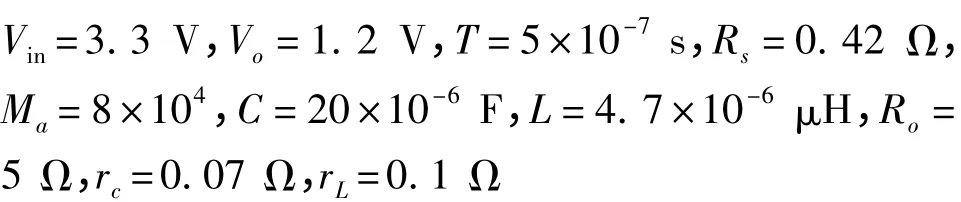
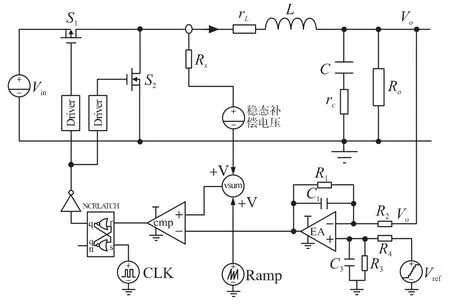
图7 Spice 验证电路框图

针对补偿模块Tc不同的直流增益G，使用Matlab 软件和Spice 电路仿真软件，对输出电压Vo瞬态响应的仿真对比波形图如图8 所示。参考电压Vref从1.2 V 阶跃到1.23 V，补偿模块的直流增益分别为25、15、9，其中15 是通过式(22)计算出的最佳增益。通过Matlab 仿真和Spice 电路仿真的输出电压瞬态响应的波形参数如表I 所示。从图8 和表1中，我们可以看出，在相同的G 值，Matlab 的仿真结果和Spice 电路验证的仿真结果非常相似。图8(b)中输出电压的锯齿波导致了和图8(a)中波形在上升时间和过冲电压值的细微差别。因为实际的开关电源是一个非线性系统，而在Matlab 的模型仿真中，被线性化和平均化了。从表1 和图8 中可以看出，当G=25 时，输出电压的响应时最快的，但是出现较大过冲和振荡。当G=9 时，输出电压的响应虽然没有出现电压过冲，但响应较慢。当G=15 时，输出电压的响应既快又没有出现电压过冲，是最佳选择。因此可以证明模型和式(22)得出的补偿模块Tc最佳直流增益是正确的。

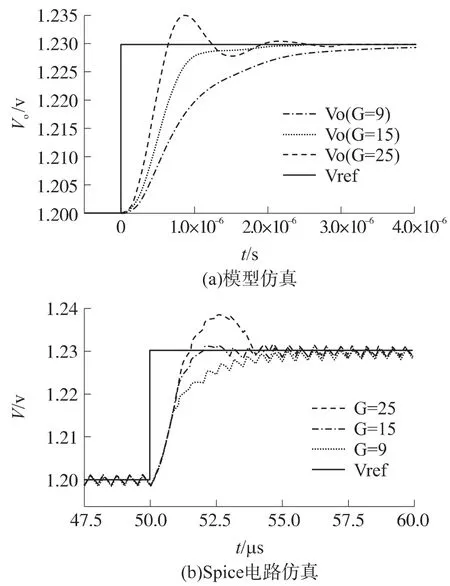
图8

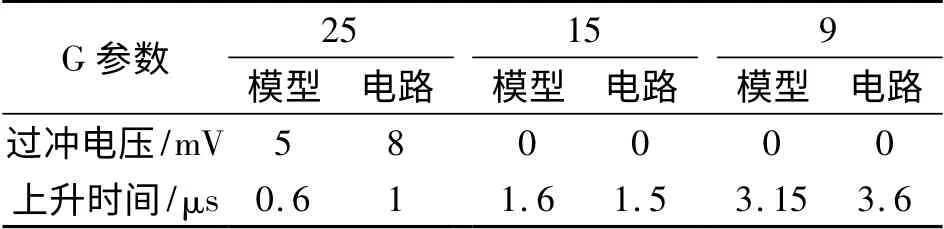
表1 Matlab 仿真和Spice 仿真的输出电压波形参数的对比

当使用DAC 技术来调节输出电压Vo从1.20 V连续阶跃到1.44 V 时，阶跃幅值为30 mV，每次阶跃持续时间5 μs，具体电路的仿真输出电压波形如图9 所示。Vo1是采用补偿模块最佳直流增益的输出电压波形，Vo2是没有采用最佳增益的输出波形。我们可以看出Vo2的波形中有许多电压过冲和毛刺，虽然它的响应比Vo1要快。因此采用优化后的直流增益的效果更好。

图9 不同直流增益下，输出电压对于参考电压Vref阶跃变化的Spice 仿真波形

4 结论

本文针对工作在高开关频率的峰值电流模式BUCK 电压源，建立了包含功率管寄生电阻和电感、电容寄生电阻的精确小信号模型。并基于此模型，设计了一个新颖的电压环路的补偿方法，即仅增加一个极点，消除输出电容寄生电阻引入的零点。在此基础上，分析了输出电压Vo对参考电压Vref的传递函数的频率响应，和补偿模块直流增益之间的关系，得出了补偿模块的最佳增益，优化了输出电压的瞬态响应。并在Spice 电路仿真中得到了验证。在需要DAC 技术调节输出电压，如给微处理器和内存供电的电源芯片中，此精确的小信号模型和频率补偿方法可以有效消除输出电压的毛刺，此方法也可以用于其他峰值电流型的电源结构中。

参考文献:

［1］ Lai Xinquan，Guo Jianping，Yu Weixue.A Novel Digital Soft－Start Circuit for DC/DC Switching Regulator［R］.ASICON 2005，554－558.

［2］ Seiya Abe，Shoyama M，Ninomiya T.First－Order Transient Response of DC－DC Converter with Peak Current Mode Control for Low－Voltage Application［J］.Power Electronics，Electrical Drives，Automation and Motion，2008，32－36.

［3］ Kaiwei Yao，Yu Meng，Lee F C. Control Bandwidth and Transient Response of Buck Converters［R］.IEEE PESC，2002，1:137－142.

［4］ Seiya Abe，Shoyama M，Ninomiya T. Optimal Design of Output Filter Capacitor for Peak Current Mode Control Converter with First－Order Response［R］.EPE ’09，1－7.

［5］ Karimi C，Godoy，Iftikhar. High Frequency Modeling of Peak Current Mode Control of DC－DC Converters［J］. Powereng，2009，146－151.

［6］ Ching Jan Chen，Dan Chen，Lee M. Design and Modeling of a Novel High－Gain Peak Current Control Scheme to achieve Adaptive Voltage Positioning for DC Power Converters［R］. IEEE PESC，2008，3284－3290.

［7］ Wu Guoying，Zhang Bo.The Whole Small Signal Model and Compensation for Regulators with Current Programmed Mode［R］.IEEE IEDST，2007，185－189.

［8］ CHEN Xiao－fei，ZOU Xue－cheng，CHENG Jun. System Modeling and Stability Design for Peak Current－mode Buck Power Converter［J］.IEEE Industrial Informatics，INDIN 2008，933－938.

［9］ Raymond B Ridley. A New，Continuous－Time Model For Current－Mode Control［J］.IEEE Trans.Power Electron，1991，8:271－280.

［10］ Marian K Kazimierczuk.Transfer Function of Current Modulator in PWM Converters with Current－Mode Control ［J］. IEEE Transactions on Circuits and Systems，2000，47(9):1407－1412.

［11］ Abraham I Pressman，Keith Billings，Taylor Morey. Switch Power Supply Design［M］.McGraw－Hill Publishers.563－564.

［12］ Mulligan J H Jr.The Effect of Pole and Zero Locations on the Transient Response of Linear Dynamic Systems［J］.Proceedings of the IRE，1949，516－529.