基于电磁仿真和测试的表面贴装器件建模
王宜辉,高建军
(华东师范大学信息学院通信系,上海200241)
对于非同轴接口器件(如表面贴装器件)的测量,必须使用测试夹具连接器件和矢量网络分析仪。因此测量结果中就包含了测试夹具带来的误差,要得到精确的器件等效电路模型,必须去嵌测试夹具。有各种方法得到器件的精确模型,比如通过精确的校准[1-2],或者通过理论得到器件的闭式方程[3]。然而,对于电小尺寸或者非均匀三维连接器(如SMA 接头)很难使用闭式方程分析器件。现在基于麦克斯韦方程的数值方法在处理复杂结构的器件建模问题中已经成为不可或缺的有用工具。近年来,计算机辅助设计用于分析任意三维连接器的问题有了长足的发展,有越来越多的电磁问题使用计算机辅助设计工具来解决[4-5]。测量法是先制造再设计,利用已经实际制造出来的元件的测量结果进行建模,关键参数通过拟合得到,可以得到各种实际的非理想效应的影响,非常可靠。
本文使用基于电磁仿真的去嵌技术去除测试夹具的影响。图1 显示了系统各参考面和各部分的散射参数定义。在待测器件的左右两边分别嵌入了连接网络,去嵌就是去除嵌入网络的影响从而得到待测器件参数的过程。对于嵌入网络参数的确定,可通过测量同等结构的标准件来实现[6]。本文通过分别测量和仿真“开路”和“短路”标准件来确定测量夹具的参数。通过HFSS 对开路和短路标准件进行仿真,仿真结果和使用矢量网络分析仪得到的测量结果进行比较,直到18 GHz 的吻合结果验证了仿真的正确性,接着就可以单独仿真测试夹具,得到测试夹具的参数。最后使用ADS 中的去嵌功能去除测试夹具的影响,使用测量法得到待测件的参数,建立待测件的等效电路模型。
1 去嵌的数值方法
去嵌是通过数学方法去除测量的待测器件数据中的多余成分,这一过程可以通过矩阵运算实现。我们可以把测试夹具和待测件看成三个二端口网络的级联,如图1 所示。St是一个2×2 的表示整体的散射矩阵,S 代表待测件的散射参数,S1和S2是2×2 的分别代表位于待测件和矢量网络分析仪之间的二端口网络的散射矩阵参数。因为是级联,将散射矩阵转换成相应的传输散射矩阵Ti(i=1,2 and t),可得

St可以通过测量得到,则Ti可以得到,如果S1和S2可以得到,则T1和T2就可以得到。从式(1)可得

然后将T 矩阵转换成S 矩阵[7],就得到了待测件的散射矩阵,现在的问题是如何得到S1和S2矩阵。
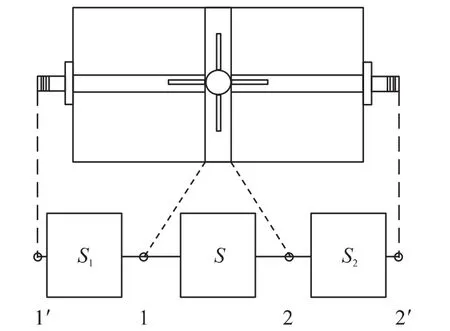
图1 测试夹具各参考面和各部分散射参数的定义
2 测试夹具参数提取
为了得到SMA 转接头和微带线部分的散射参数,我们首先将测量的“开路”和“短路”结构参数和仿真的参数进行比较,以验证了仿真的准确性。图2 所示为“开路”和“短路”标准件,测试夹具外围金属材料是可伐金,金属的内部尺寸是30 mm×25 mm×12 mm,两边的微带线具有对称结构,其尺寸为12.5 mm×1.5 mm×0.02 mm,基片的材料是Rogers 5880,具有介电常数Er=2.2 和厚度0.5 mm。对于这个尺寸,微带线的特性阻抗为Zc=50 Ω。“短路”标准件与“开路”标准件类似,只是终端通过金属化通孔接地。矢量网络分析仪(Agilent 8363c)使用SOLT 校准方法校准到与SMA 的接触面。图3 所示分别为“开路”和“短路”标准件的测试数据和仿真数据的比较,通过幅度和角度的比较,可以看出直到18 GHz 测试和仿真吻合良好,其中相位的吻合更为重要,因为相位更易受到各种干扰,而超过18 GHz吻合度降低,因为SMA 接头的最高工作频率既是18 GHz,超过此频率的测量结果本身就是不可靠的。这一吻合结果验证了仿真中所建立的测试夹具模型的准确性。

图2 “开路”和“短路”标准件
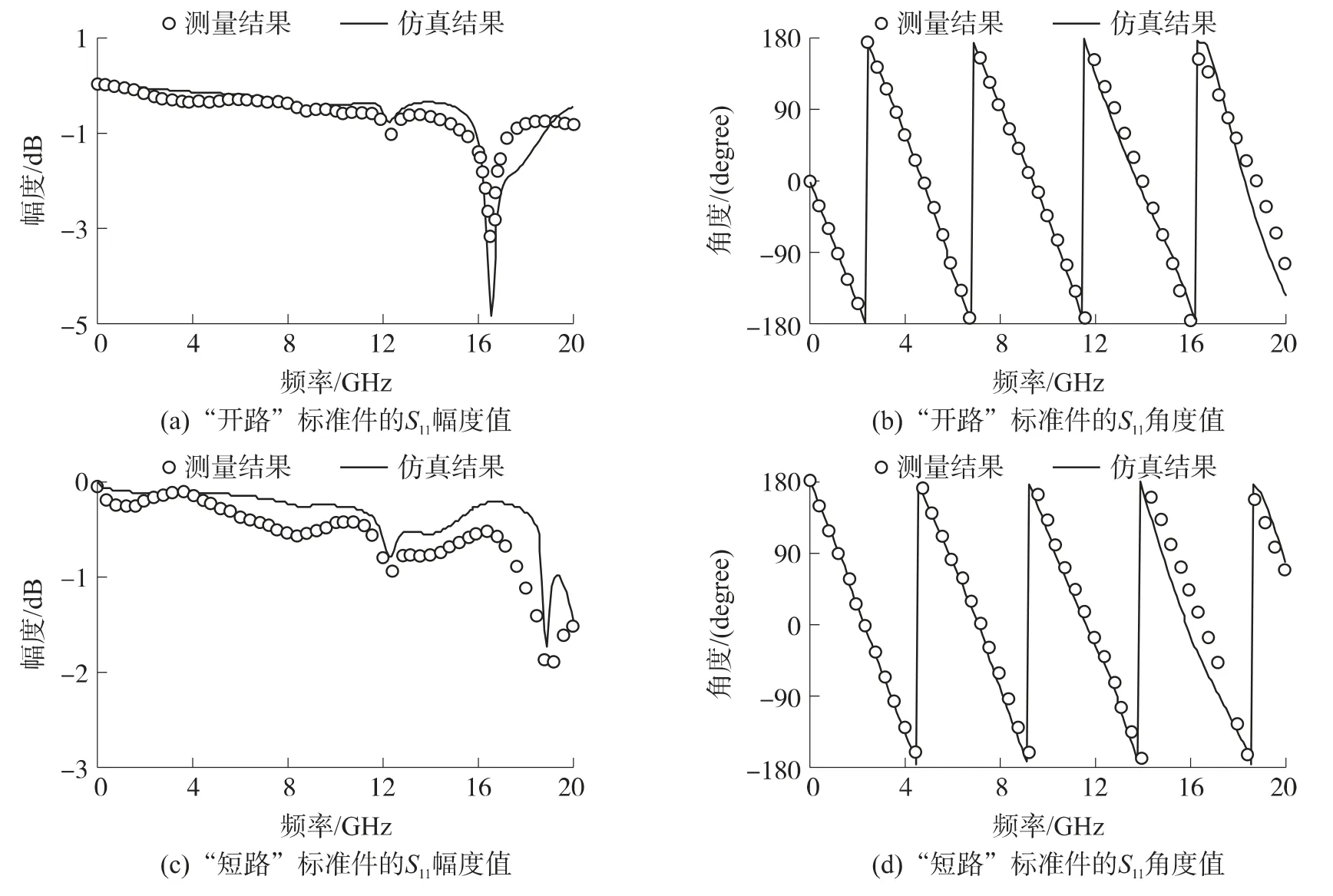
图3 “开路”和“短路”标准件的测试数据和仿真数据的对比
3 表面贴装电阻的参数提取
电阻的高频等效电路模型由图4 所示。本文以标称值为100 Ω 的电阻为例进行参数提取。
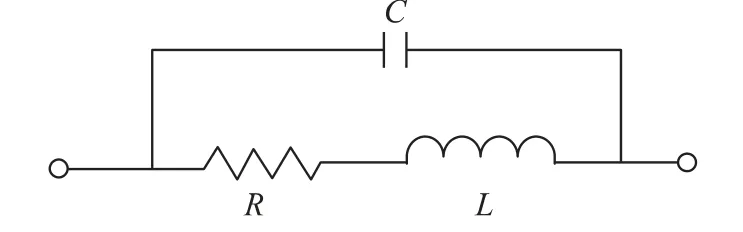
图4 电阻的高频等效电路模型
在这种情况下,电阻的输入导纳可以表示为:
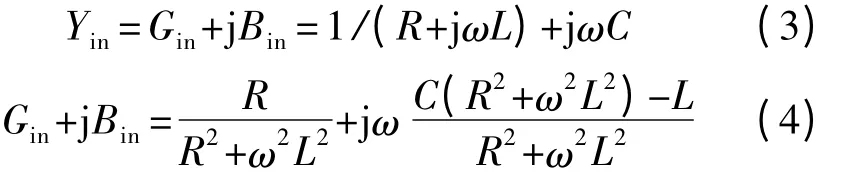
在谐振点(i.e.,Bin=0),输入阻抗为

从图5 等效电路中的R 值可以在低频提取,L 和C可以表示为式(6)和式(7)。
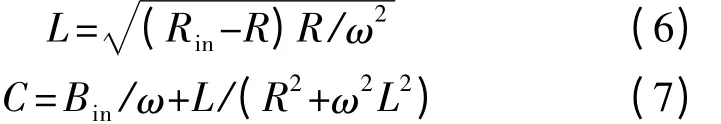
因此R、L、C 可以从式(5)、式(6)和式(7)中提取出来。使用ADS 可以得到R、L 和C 的曲线,分别由图5、图6 和图7 所示。
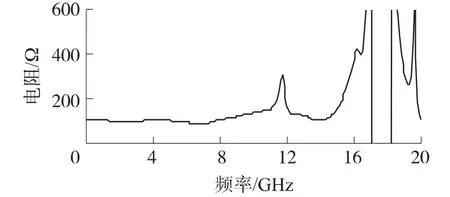
图5 电阻等效电路中参数R 的曲线
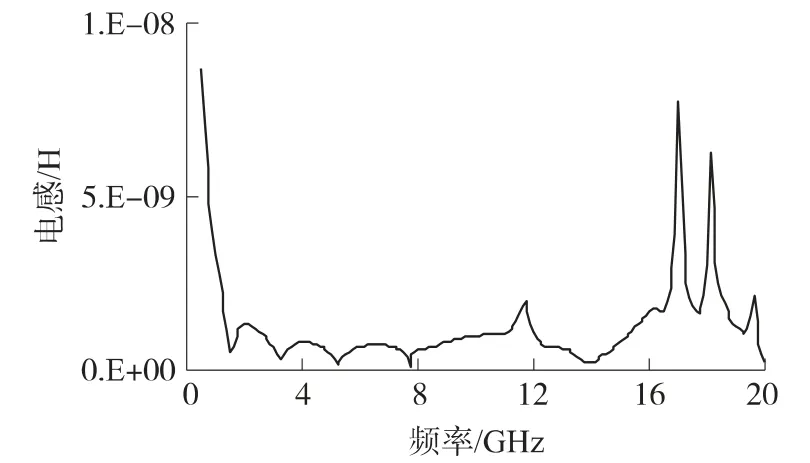
图6 电阻等效电路中参数L 的曲线

图7 电阻等效电路中参数C 的曲线
提取出R、L 和C 的值后使用ADS 进行仿真。仿真电路图如图8 所示。图9 显示了基于测量和ADS 仿真的电阻散射参数,可以看出直到10 GHz结果吻合良好。

图8 ADS 中100 Ω 电阻的等效电路模型
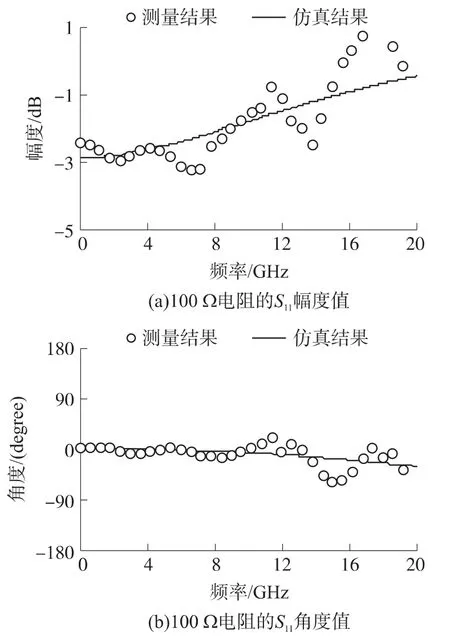
图9 基于测量和ADS 仿真的电阻散射参数比较
4 结论
本文使用基于电磁仿真的方法去除测试夹具的影响,再使用测量法提取表面贴装器件的参数建立模型。所建立的模型能够在很宽的频率范围内表征器件(高达10 GHz)。这一方法避免使用复杂的校准方法,(只需使用标准的SOLT 方法校准)且能够在很宽的频率范围表征器件。
[1] Kompa G,Schlechtweg M,van Raay F. Precisely Calibrated Coaxial-to-Microstrip Transitions Yield Improved Performance in GaAs FET Characterization[J]. IEEE Transactions on Microwave Theory and Techniques,1990,38(1):62-68.
[2] Roger B Marks.A Multiline Method of Network Analyzer Calibration[J]. IEEE Transactions on Microwave Theory and Techniques,1991,39(7):1205-1215.
[3] Krishna Naishadham,Tahsin Durak. Measurement-Based Closed-Form Modeling of Surface-Mounted RF Components[J]. IEEE Transactions on Microwave Theory and Techniques,2002,50(10):2276-2286.
[4] Randus M,Hoffmann K.Design of SMA 50 Ω Load Using 3D EM Field Simulator:Comparison with Reality[C]//COMITE 2008.14th Conference on Microwave Techniques.2008.
[5] Chramiec J,Janiczak B,Komisarczuk J,et al.CAD Models of Connectors and Transitions used in Hybrid Microwave Integrated Circuits[C]//28th European Microwave Conference.1998.
[6] Riddle A.Microwave Circuit Modeling Using Electromagnetic Field Simulation(Book Review)[J]. IEEE microwave magazine,2004,5:88.
[7] Frichey D A. Conversions between S,Z,Y,H,ABCD,and T Parameters which are Valid for Complex Source and Load Impedances[J]. IEEE Transactions on Microwave Theory and Techniques,1994,42(2):205-211.

