栅格式方孔翅片自然对流换热的数值模拟*

黄秋月，孙志坚 ，纪翠娟，陈 然

(浙江大学能源工程学系，杭州310027)

电子器件的寿命和可靠性与温度密切相关，高温严重影响电子器件的使用寿命和可靠性，如:LED(发光二极管)是温度敏感器件，结温的升高将造成其寿命缩短、光衰等性能和封装结构的问题［1－3］。电子器件散热得到越来越多的重视，虽然许多文章研究采用强迫冷却方式对电子器件进行散热［4］，但是自然冷却由于其工作稳定可靠、节能环保等许多被动冷却方式无法取代的优点［5］，还是被用于电子器件冷却，其中自然对流状态下的翅片散热器由于其工作稳定可靠被广泛应用。国内外很多学者对翅片散热器进行了大量的理论与实验研究:Morega 等人［6］研究了自然对流中最优化的平板型翅片的排列方式，指出100＜Re＜10 000 时，等距排列的平板型翅片，散热效果最好。Vollaro 等人［7］研究在自然对流中，平板型翅片的优化设计，得出了换热量与翅片间距的关联式。Harahap 等人［8］实验对比了5 种形式的散热翅片，结合无因次相似分析研究翅片间距、长度、厚度的改变对散热的影响，指出翅片间距与长度是影响散热效果的主要参数。罗晓斌等人［9］采用实验和数值模拟的方法设计并优化了水平板翅片散热器。Narasimhan等人［10］用CFD 数值模拟软件模拟分析了自然对流中平板型翅片与柱状翅片的散热效果，用紧凑式翅片的方式并结合Nu 数和Ra 数做了讨论，结果表明这种紧凑式翅片可以降低网格数目、节省运算资源和时间，而且可以清楚分析出入口的温度分布和速度流场。A.Bar－Cohen［11］对集成电子器件的自然对流散热进行研究，探讨并比较了不同的散热方式。王乐［12］等人对自然对流条件下LED 阵列散热器进行改进，提出开缝翅片可以提高散热器的性能。

然而，随着电子器件的高功率化和小型化，热流密度越来越高的小空间散热问题亟待解决，板翅式散热器逐渐不能满足热管理的要求。因此，本文提出了一种新型结构的栅格式方孔翅片散热器，采用Fluent软件进行数值模拟，它具有两方面优势:①优化的方孔尺寸可大大增加翅片与空气的接触面积;②改变空气的流动方向，通过扰流作用强化表面换热。

1 物理模型及理论分析

应用于电子器件散热的被动散热器大部分由基板和若干肋片组成。图1 为栅格式方孔翅片散热器的物理模型图，其中:H 为翅片高度，mm;S 为翅片间距，mm;δ 为翅片厚度，mm;b 为孔边长，mm;L 为基板长度，mm;W 为基板宽度，mm;B 为基板高度，mm;c为孔横向间距，mm;e 为孔纵向间距，mm;与同尺寸板翅式翅片相比，方孔翅片具有两方面作用:改变翅片与空气接触面积、改变空气流向起扰流作用。每个栅格式方孔增加翅片与空气的接触面积为4bδ，同时减少2b2的面积，所以b/δ=2 是临界比，当b/δ＜2 时，栅格方孔翅片面积大于板翅式翅片;当b/δ＞2 时，栅格方孔翅片面积小于板翅式翅片。通过对国内外目前应用于电子器件散热翅片几何因素的研究［3，11］，并考虑实际工程应用，把翅片尺寸范围定为:H=20 mm ～120 mm，S=10 mm ～60 mm，L=62 mm ～372 mm，W=40 mm ～240 mm，δ=2 mm ～4 mm，b=1 mm ～8 mm。

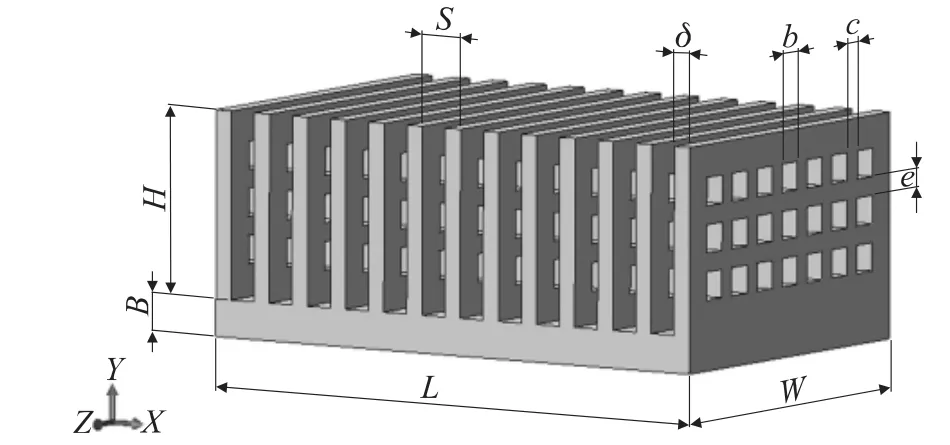
图1 栅格式方孔翅片散热器模型

栅格翅片散热器中自然对流换热与很多因素有关，用数值计算的方法解决这一传热问题，必须先通过量纲分析法得到无量纲准则数以减少变量，从而减少计算工作量。因此，我们首先通过理论分析来确定这些影响因素。

根据理论研究［13－15］，对栅格翅片散热器中的自然对流换热作以下假设:

(1)散热器材料均匀，各向同物性;

(2)基板和翅片的内部传热过程是稳态、无内热源的三维导热，物性参数仅考虑温度的影响;

(3)空气的密度与压力无关，并忽略很小的压力功;

(4)采用Boussinesq 模型，除了动量方程的浮力项之外，连续性方程和能量方程中将密度看成常数。

(5)忽略粘度耗散热所引起的温度变化;

根据以上假设，可得到描述稳态自然对流换热过程的基本方程组:

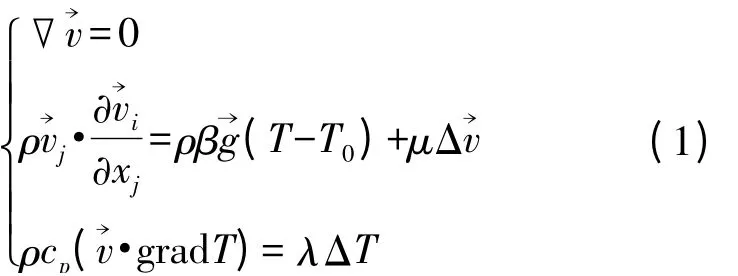
边界条件为:

(1)基板底面为第2 类边界条件:

(2)方孔翅片表面为第3 类边界条件:

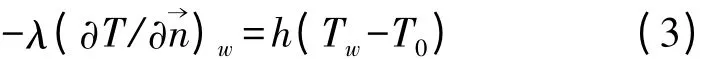
定义平均换热系数h 为:

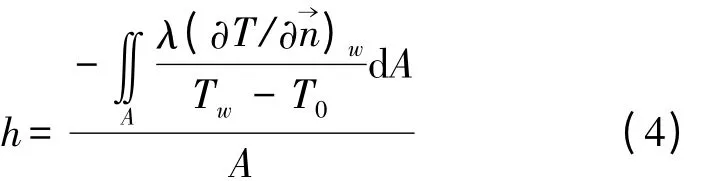
式中:Tw为基板底面壁温;A 为方孔翅片散热器的表面积。

那么

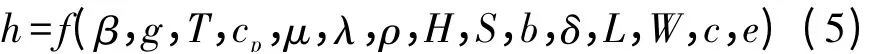
由上式可见，影响栅格式方孔翅片换热性能的物理量有15 个，问题很复杂，为简化计算，可根据∏原理，进行以下无量纲化:

β、g、T、μ、ρ、H 组成格拉晓夫数Gr，特征尺寸取翅片高度H;λ、cp、μ 组成普朗特数Pr，对空气，取Pr=0.698;将翅片高度H 和翅片间距S 之比H/S 以及孔边长b 和翅片厚度δ 之比b/δ 作为两个无量纲参数;为了突出影响方孔翅片自然对流的主要因素，在满足导热热阻要求下，较小的c，e 值有利于强化对流热，针对本文研究范围，取c=e=2 mm;散热基板厚度B对散热的影响较小，取定值B=4 mm;因与H/S、b/δ的影响比较，L、W 引起的边缘效应可忽略。

因此描述对流换热情况的Nu 可表示为:

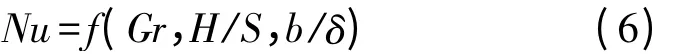
综上所述，对栅格翅片散热器的自然对流的研究就可以简化为求解一定范围H/S 和b/δ 时的Gr与Nu 之间的关系。

2 计算结果与分析

(1)图2 为H/S=2 时，Gr 数和b/δ 对Nu 数的影响图。从图中可看出:b/δ=0.5 ～1.5 3 种情况的Nu数比b/δ = 0 即板翅式翅片时的Nu 数平均小16.57%、11.936%、4.739%;b/δ=2 时比b/δ=0 时减小0.016%;而当b/δ=2.5 ～4 4 种情况的Nu 数相比b/δ=0 分别增大18.39%，20.21%，25.60%，8.86%。比较相同Gr 数时的Nu 数大小可以比较相同模型时的平均对流换热系数h 的大小，即:相比b/δ=0，b/δ=0.5 ～1.5 会减小平均对流换热系数h，b/δ=2 基本不影响h，而b/δ=2.5 ～4 会增大h，特别注意，当b/δ=3.5 时，h 增大到最大值。

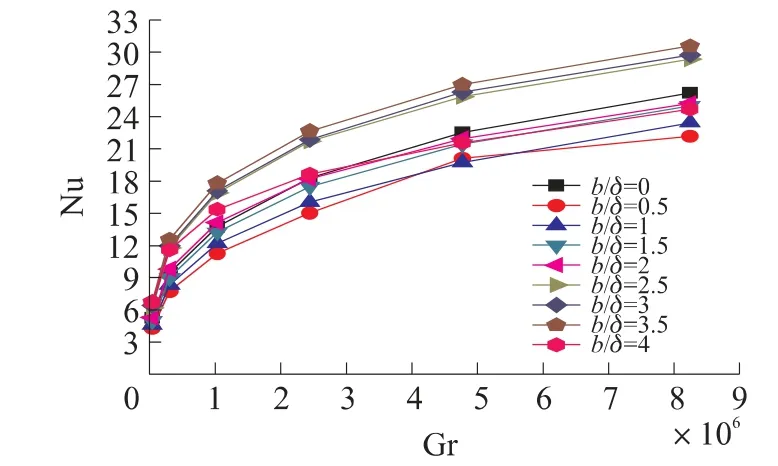
图2 H/S=2 时，Gr 数和b/δ 对Nu 数的影响

从这些模拟结果中还可以看出，翅片上开孔会同时影响表面换热面积A 和平均对流换热系数h，对于相同模型，小的孔边长b 比大的孔边长b 更能增大方孔翅片散热器表面积A，但同时减小了对流换热系数的h 值。

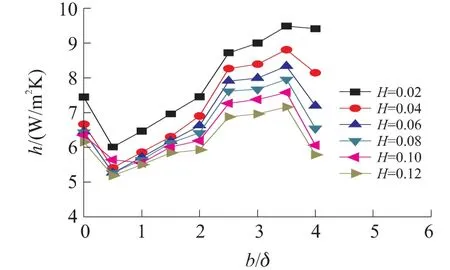
图3 设计工况下，方孔翅片高度H 和边厚比b/δ对平均对流换热系数h 的影响

(2)图3 为设计工况:Pr = 0. 698，Twmax≤70℃，T0=25 ℃时，选择H/S=2，H=20 mm ～120 mm 条件下，方孔翅片高度H 和边厚比b/δ 对平均对流换热系数h 的影响。对于特定H，h 随b/δ 变化的趋势相同，与b/δ=0 相比，b/δ=0.5 时的h 陡降，b/δ=0.5 ～1.5 呈直线上升，b/δ=2 基本与b/δ=0 持平，b/δ=2.5～3.5 持续增大，b/δ=4 减小;b/δ=3.5 时的h 最大，这与图2 所得结论相吻合。

从图中还可以看出，对于相同模型，低翅片比高翅片有更大的对流换热系数。分析上述结果:打孔会同时影响表面换热面积和平均对流换热系数，对于相同模型，孔边长小比孔边长大更能增大表面换热面积A，但增加出来的孔的内部面积与空气的对流换热系数相对于未开孔时的竖直壁面与空气的对流换热系数或增大或减小，导致平均对流换热系数h 或增大或减小。

(3)研究针对有限空间情况通过改变H/S 来强化翅片的散热。图4 为该种情况下，当b/δ=3/2 时，Gr 数和高距比H/S 对Nu 数的影响图。从图4 可以看出:Nu 数随Gr 数增大而增大，随着H/S 的增大，H/S=4/3，5/4，2，8/3，10/3，4，16/3 比H/S=1 时的Nu 数 分 别 增 大－ 1. 91%，－ 2. 68%，－ 3.645%，－5.59%，0.067%，－8.45%，－32.85%。负号表示Nu 数减小;

图4 b/δ=3/2 时，Gr 数和H/S 对Nu 数的影响

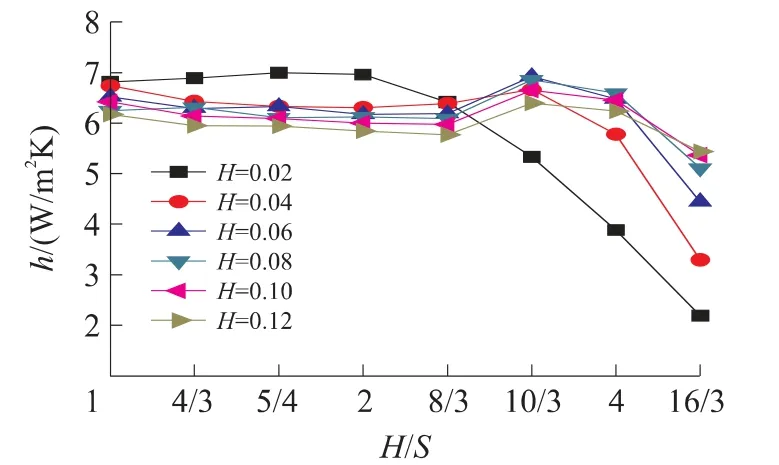
图5 设计工况下，高距比H/S 对流换热系数h 的影响

(4)通过研究LED 芯片处在正常的工作状况:Pr=0.698，Twmax≤70 ℃，T0=25 ℃时，在b/δ=3/2时，H=20 mm ～120 mm 条件下，翅片高距比H/S 与对流换热系数h 的影响图，得到图5。从图5 可以看出:当b/δ 和H 一定时，随H/S 的增大，S 减少，即有限空间时增加翅片个数，表面换热面积不断增大。对于H=0.04 m ～0.12 m 范围，当H/S=1 ～8/3 时，对流换热系数h 随H/S 的增大变化不大，说明增大H/S 会增大换热量;当H/S=8/3 ～10/3 时，h 陡增;当H/S=10/3 ～16/3 时，h 递减，说明增加H/S 虽然使换热面积增大，但由于S 过小，对流换热系数h 急剧减小。对于H=0.02 m 时，当H/S=1 ～2 范围，h逐渐增大，此时为强化散热;当H/S=2 ～16/3 范围，h 递减。对于h 减小的情况，最终能否强化散热要看h 的减小与A 的增大之间的平衡。

(5)图6 为LED 芯片正常工作条件下，方孔翅片高度H 和边厚比b/δ 对散热量Q 的影响图。从图6 可以看出:相同b/δ 时，随着H 的增加，散热量Q 增加;与b/δ=0 比较，当b/δ=2.5 时，Q 为最大，平均增加15%，此时打孔对于散热面积A 和表面换热系数h 的影响达到对散热的最佳效果;当b/δ=4时，Q 显著下降;而且相比b/δ=0，b/δ=2.5 时，高度H 越大，Q 的增幅越大，而b/δ=4 时，高度H 越大，Q的降幅越大，也就是当翅片越高时，合适的打孔对于散热的增减影响明显。

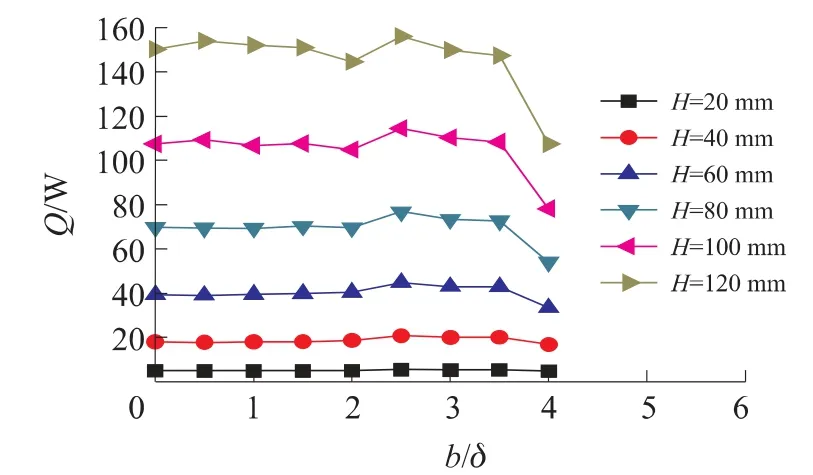
图6 设计工况一下，方孔翅片高度H 和边厚比b/δ对散热量Q 的影响

3 实例与验证

研究一个具体栅格式方孔翅片散热器:基板长度L=62 mm，基板宽度W=40 mm，基板厚度B=4 mm;翅片厚度δ=2 mm，翅片高度H=20 mm，翅片间距S=10 mm，开孔边长b=5 mm，孔间横向间距c 和纵向间距e 均为2 mm;热沉的最高温度为70 ℃时，此时格栅式方孔翅片散热器的散热量为5.597 W，而相同尺寸时没有开孔的板翅式散热器为5.045 W。可见，相同尺寸大小的栅格式方孔翅片散热器比板翅式散热器的散热量大11%。说明通过优化设计，与同尺寸时的板翅式散热器相比，栅格式方孔翅片散热器会有更佳的散热效果。计算可得此栅格式方孔翅片散热器的Gr=3.81×104，Nu=8.69，从图2 读出Pr=0.698，H/S=2 时，b/δ=2.5 时，Gr=3.81×104，Nu=8.721 659，Nu 数的误差为0.36%。

采用本文的数值模拟方法，对照罗晓斌教授等人［8］采用翅片高度为17 mm，翅片厚度为2 mm，翅片间距为5 mm 的直翅片自然对流换热试验。实验采用大功率LED 基板的最高温度为45 ℃。数值模拟基本的最高温度为42.45 ℃，误差为5.67%。该数值模拟方法误差较小。所以文章以上的模拟结果可靠，可用于指导工程实际应用。

4 结论

(1)本文提出一种新型翅片散热器:栅格式方孔翅片散热器;通过建立描述对流过程的方程组及定解条件，根据量纲分析法确定了影响该种翅片散热器中自然对流换热性能的主要无量纲参数，得出Nu=f(Gr，H/S，b/δ)关系表达式。

(2)得出了H/S=2、b/δ=0 ～4 时准则数Gr－Nu的关系图，适用范围较大;研究了设计工况下方孔翅片高度H 和边厚比b/δ 对平均对流换热系数h 的影响。

(3)研究了在有限空间内通过改变H/S 来强化翅片散热，根据有限空间的散热要求，得出了在b/δ=1.5、H/S=1 ～16/3 时的准则数Gr－Nu 的关系图。

(4)实例结果验证表明，通过优化设计，新型翅片散热器教板翅散热器更好的散热效果，相同尺寸大小的栅格式方孔翅片散热器比板翅式散热器的散热量大11%;

(5)本文的结论及两个Nu－Gr 数关系图对于工程实际运用具有理论指导意义，本文研究结果可为温度敏感电子器件，如LED(发光二极管)照明等的散热设计提供理论依据。

［1］ Arik M，Peitroski J，Wwaver S. Thermal Challenges in the Future Generation Solid State Lighting Applications:Light Emitting Diodes［C］//Eighth Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic System，2002:113－120.

［2］ Huh C，Schaffw J，Eastmanl F. Temperature Dependence of Performance of InGaN/GaN MQW LED Switch Different Indium Compositions［J］.IEEE Electron Device Lett，2004，25(2):424－426.

［3］ 刘红，赵芹，蒋兰芳，等.集成式大功率LED 路灯散热器的结构设计［J］.电子器件，2010，8，33(4):481－484.

［4］ 刘衍平，高新霞.大功率电子器件散热器系统的数值模拟［J］.电子器件，2009，8，32(4):850－854.

［5］ 徐婷婷，吴玉庭，马重芳.不同环境中翅片散热器性能的仿真研究［J］.电子器件，2009，8，32(4):850－854.

［6］ Morega M，Bejan A，Lee S W. Free Stream Cooling of a Stack of Parallel Plates［J］.Heat Mass Transfer，1995，38(3):519－531.

［7］ Vollaro A，Grignaffini S，Gugliermetti F.Optimum Design of Vertical Rectangular Fin Arrays［J］.Int.J.Thermal Sciences，1999，38(6):525－529.

［8］ Harahap F，Setio D. Correlations for Heat Dissipation and Natural Convection Heat－Transfer from Horizontally－Based，Vertically－Finned Arrays［J］.Applied Energy，2001，69(1):29－38.

［9］ Luo Xiaobing，Xiong Wei，Cheng Ting，et al.Design and Optimization of Horizontally－Located Plate Fin Heat Sink［C］//Electronic Com－ponents and Technology Conference，2009:854－859.

［10］ Narasimhan S，Majdalani J.Characterization of Compact Heat Sink Models in Natural Convection［J］.IEEE Transactions on Com－ponents and Packaging Technologies，2002，25(1):78－86.

［11］ Bar－Cohen A. Optimal Natural－Convection Cooling of Electronic Assemblies［C］//ASME Design Engineering Conference，Chicago，USA，1977，May:9－12.

［12］ 王乐，吴珂，俞益波，等.自然对流条件下LED 阵列散热器改进研究［J］.光电子·激光，2011，3，22(3):338－342.

［13］ 陶文铨.数值传热学［M］. 陕西:西安交通大学出版社，1988:195－226.

［14］ Paisarrn Naphon，Setha Klangchart，Somchai Wongwises.Numerical Investigation on the Heat Transfer and Flow in the Mini－Fin Heat Sink for CPU［J］. International Communication in Heat and Mass Transfer，2009(36):834－840.

［15］ Rana P，Bhargava R. Numerical Study of Heat Transfer Enhancement in Mixed Convection Flow Along a Vertical Plate with Heat Source/sink Utilizing Nanofluids［J］. Commun Nonlinear Sci Numer Simulat，2011(16):4318－4334.