基于分水岭与图割的自动分割方法

刘 荣

(北京航空航天大学 机械工程及自动化学院，北京100191)

彭艳敏

(天津医科大学 医学影像学院，天津300203)

唐 粲 程 胜

(昆山市工业技术研究院，昆山215300)

Liu Rong

(School of Mechanical Engineering and Automation，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

Peng Yanmin

(School of Medical Imaging，Tianjin Medical University，Tianjin 300203，China)

Tang Can Cheng Sheng

(Kunshan Industrial Technology Research Institute，Kunshan 215300，China)

随着计算机可视化信息的发展，机器人辅助视觉定位手术越来越多的应用到临床上.图像分割不仅是医生诊断的基础，还是视觉定位的关键.医学图像由于人体复杂的特殊性，很多通用的图像分割算法对医学图像并不适合，都有一定的局限性.区域增长［1］、分裂合并［2］等方法都是基于区域的信息，虽然简单，但提取出物体的边界模糊.基于活动轮廓［3］的算法如snakes、变形和最短路径法是基于边界的，很难扩展到三维空间上.文献［4］提出基于边界和区域的算法，即图割，能够很好的提取出物体的边界，在计算机视觉方面发挥越来越重要的作用.但该文献在寻找最小能量的过程中是基于像素的，存在海量计算问题.文献［5］提出的分水岭算法一般都存在过分割现象，提取出的物体没有太多实际意义，通常还需要区域合并.但分水岭算法能够很好的定位对象的边缘，并且能够保持每个小区域中的微小差异［6］.

本文对内外轮廓之间的图像进行预分割后，对分割后的小区域利用图割进行分割，由对每个像素操作变成对小区域操作;通过实验验证本文算法在运行时间和运行效果上都优于文献［7］.

1 算法基础

1.1 图割的相关理论

图像分割可以转换成求解能量函数最小值问题.图割是利用图论中的最小割算法求能量函数全局最优解的算法.利用图割来解决问题需要做到以下3点:

1)构造图结构.把一幅图像转变成有向图G或者无向图，图的顶点为图像中的每个像素点，两个相邻像素在图中表示为一条边，像素之间的亮度、梯度等信息可以转变成边的容量.

2)构造能量函数.图割综合了边界和区域的信息，图像分割问题可以转换为求取使能量函数取到极小值时的标号场.该能量函数一般形式可以表示为

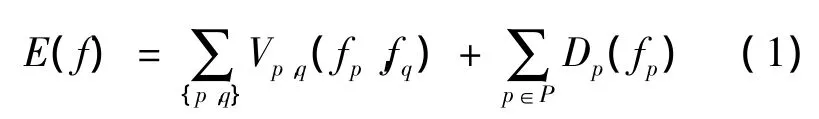
其中，Vp，q(fp，fq)表示平滑项能量，是对不连续性的一种惩罚，为相邻像素之间能量;Dp(fp)是数据项能量，是对当前标号与观测数据间不符合程度的一种惩罚.

3)利用最大流/最小割求解能量函数全局最小值.得到的能量函数的最小值就是对图像的精确分割结果.在1.3节详细介绍本文采用的最大流/最小割算法.

1.2 多源点多汇点简化图

一幅图像可看作有向图 G=〈V，ε〉，其中V是顶点集，代表图像中的每个像素，ε是相邻顶点之间边的集合，即邻接边的集合.对多源点到多汇点的有向图，可以采用文献［7］中把多个节点简化成一个节点，汇合边的容量，删除多余边简化图结构的方式，即把一系列的源点 Vs={s1，s2，s3，…，sn}简化成一个新的节点V1，把一系列的汇点Vt={t1，t2，…，tn}简化成一个新的节点 V2，对于每一个与源点相连的节点，其边的容量为所有与源点相连边的容量之和，同理与汇点相连的节点的容量，为这个节点与所有汇点相连边的容量之和.这样有向图G简化成一个新的有向图G′=〈V′，ε′〉，其中 V′=V －Vs－ Vt+V1+V2.对有向图G=〈V，ε〉和它的简化图 G′=〈V′，ε′〉进行最大流/最小割求得最小能量是相同的，文献［7］已给出相关证明.图1为多源点和多汇点图，根据上述规则可以简化成单源点和单汇点图，如图2所示.

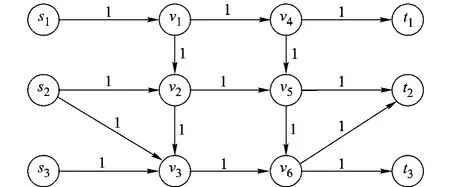
图1 多源点和多汇点图

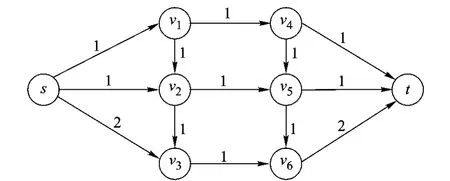
图2 简化源点和汇点后的图

1.3 最大流/最小割

最大流/最小割算法是用来求流量网络的最小能量或近似最小能量的算法.给定一个流量网络G=(V，ε)，V是顶点集，ε是相邻顶点边的集合，源点s，汇点t，f是边的流量函数.

最大流/最小割的基本思想:分别以源点s和汇点t来构造搜索树S和T，通过生长树S和T来寻找增广路径［8］.它可以分成4步来做:

1)寻找增广路径(growth stage);

2)处理增广路径(augmentation stage);

3)组合深林成树(adoption stage);

4)若步骤1)中寻找不到增广路径，则找到最小割，算法退出;否则，继续步骤1)～步骤3).

由上述算法思想可以找到一条从源点s到汇点t的增广路径，如图3所示.与源点和汇点均不相连的点被归为背景区域.

图3 从源点s到汇点t的一条路径

1.4 分水岭算法

分水岭分割思想来源于地形学，在众多现有的顺序分水岭算法中，Vincent与Soille在1991年提出的基于沉浸模拟的算法是最有效的算法，也是目前应用最广的算法.把图像看作地形学上被水覆盖的自然地貌，将图像中各点的梯度值视为该点的高度，在图像的每个区域的最小值的位置打一个洞，然后向图像形成的地表面中缓慢注水，水面将逐渐浸没地面，从而形成一个个集水盆地.在来自两个不同集水盆地的水将要发生汇合，则在汇合处建一水坝.在浸没过程的最后，每个集水盆地最终都会被水坝包围.集水盆地的边界，也就是水坝，则为图像的分水岭.

算法分为排序和泛洪两部分.文献［5］中有相关算法的伪代码.

2 基于图割和分水岭的算法

利用分水岭和图割对图像进行分割，算法步骤如下:

1)在待分割的目标物体内用框图选择一个区域，作为内轮廓I;

2)用框图框住待分割的物体，作为外轮廓O;

3)从内轮廓到外轮廓，利用分水岭对图像进行预分割，从而得到一系列的小区域;

4)把含有内轮廓的小区域作为源点s，含有外轮廓的小区域作为汇点t，两相邻像素间的流量关系为f，转换成单源点和单汇点，构成新的图G;

5)用最大流/最小割求解图的最小能量.

图4～图10为算法的执行步骤.其中图5为了方便后面的运算假设了图中的区域标号.

2.1 图像预处理分割建立图结构

图4 内轮廓和外轮廓

图5 对图像进行预处理

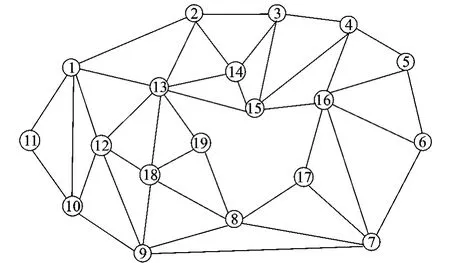
图6 对于分割后的区域建立图结构

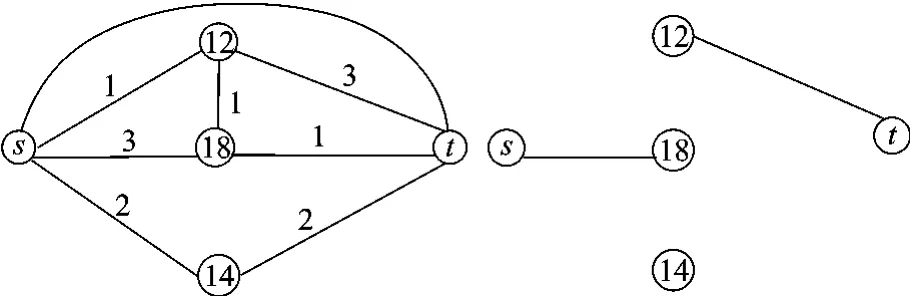
图7 单源点和单汇点图 图8 最大流/最小割

图9 切割图(虚线为切割线)

图10 分割图

利用分水岭算法对内外轮廓之间的区域进行预分割后，根据这些分割后的小区域建立新的图结构G.

首先设置一个二维数组L(l，w)=3，记录图像中每个点初始状态下的标号，默认状态下每个点的标号为3，l和w分别为图像的长度和宽度.选择待分割物体的内轮廓，同时设置L(i，j)=0，(i，j)为内轮廓上的任意一个像素的位置;选择待分割物体外轮廓，同时设置 L(i，j)=1，(i，j)为外轮廓上的任意一个像素的位置.内外轮廓之间的区域L(i，j)=2为待分割区域，则 L(i，j)∈{0，1，2，3}.L(i，j)=3 的区域将不予考虑.

应用分水岭算法对图像L(i，j)=2的区域进行预分割后，图像会分成n个小区域，每个小区域具有不同的标号 f［k］，k=1，2，…，n，对这些小区域建立图结构，即寻找每个小区域邻接区域的过程，算法步骤如下:

1)k=1;

2)对标号为k的区域，遍历所有标号为k的元素，并寻找它们的邻接点，如果邻接点的标号为x，那么标号为k的区域就和标号为x的区域邻接;遍历完标号为k的区域，找到其所有的邻接区域;如果标号为k的区域中的像素存在L(i，j)=0的像素点，那么标号为k的区域就是源点;如果存在L(i，j)=1，那么标号为k的区域就是汇点;这样可以遍历下一个标号的区域;

3)k=k+1，如果 k＞n，算法结束，否则转向步骤2)继续寻找下一个标号的邻接点.

对内外轮廓之间的区域进行预分割后，根据每个区域的邻接区域关系建立新的图G，建立各个节点的邻接表.

2.2 边的流量

图像中的边的邻接关系一般用4邻域或者8邻域表示.为了避免二义性，本文边的邻接关系采用8邻域表示法.相邻顶点之间的边的流量值代表相邻顶点之间的相似度.本文采用文献［8］中边的容量公式:

其中 g(i，j)=exp(－gij(i)/maxk(gij(k)))gij(k)表示从i到j第k个像素的梯度幅度值，maxk(gij(k))表示最大的梯度幅度值;在预分割后的图像中，gij(i)表示第i个区域所有像素的梯度幅度值的均值;C(i，j)表示两个相邻区域i和j的容量.

2.3 三维分割

在机器人辅助视觉定位系统中，重建出三维的病灶或人体组织，可以帮助医生诊断病情，确定规划路径.三维分割和二维分割类似，算法如下:

1)第i张CT图像上，利用本文二维分割的算法提取出轮廓，保存这个轮廓为Bi，i=1;

2)把轮廓Bi映射到第i+1张CT的图像上，把Bi+w作为外轮廓Oi+1，Bi－w作为内轮廓Ii+1;

3)在内外轮廓之间利用本文算法对第i+1张CT分割，提取轮廓Bi+1;

4)i=i+1;重复步骤2)～3)的过程，直到遍历完所有的CT图像.

通过步骤1)～4)可完成对图像的三维分割，然后把所提取出来物体的轮廓重建出三维物体.

3 实验与分析

本文算法是由C++和Matlab实现的，所有的实验结果都是在同一台计算机上实现的，配置为:2 GB内存，Intel(R)Core(TM)2 Duo处理器，XP操作系统.

3.1 二维分割

使用本文算法对一系列图像进行分割，并在分割效果和运行时间上与文献［7］相比较.图11为应用本文算法对图像分割的效果图，图12为文献［7］中算法对图像分割的效果图.由图11、图12知，本文算法对图像的分割效果优于文献［7］.同时，文献［7］对初始轮廓的选择很敏感，如果初始轮廓严重偏离待分割的物体，提取出的轮廓和待分割的物体相差很大;如果初始轮廓已经很接近待分割物体，提取出物体的轮廓比较好.而本文算法，只要选择的内轮廓在待分割物体上，外轮廓在待分割物体上的外面，就可以提取出待分割物体的轮廓，因此本文算法受初始轮廓的影响较小.

表1为2种算法的运行时间比较，可见，本文的算法要远远超过文献［7］算法的效率.算法的运行时间还和初始轮廓提取有关，当内外轮廓之间的区域比较大时，算法耗时较长，当内外轮廓之间的区域比较小时，耗时较短.

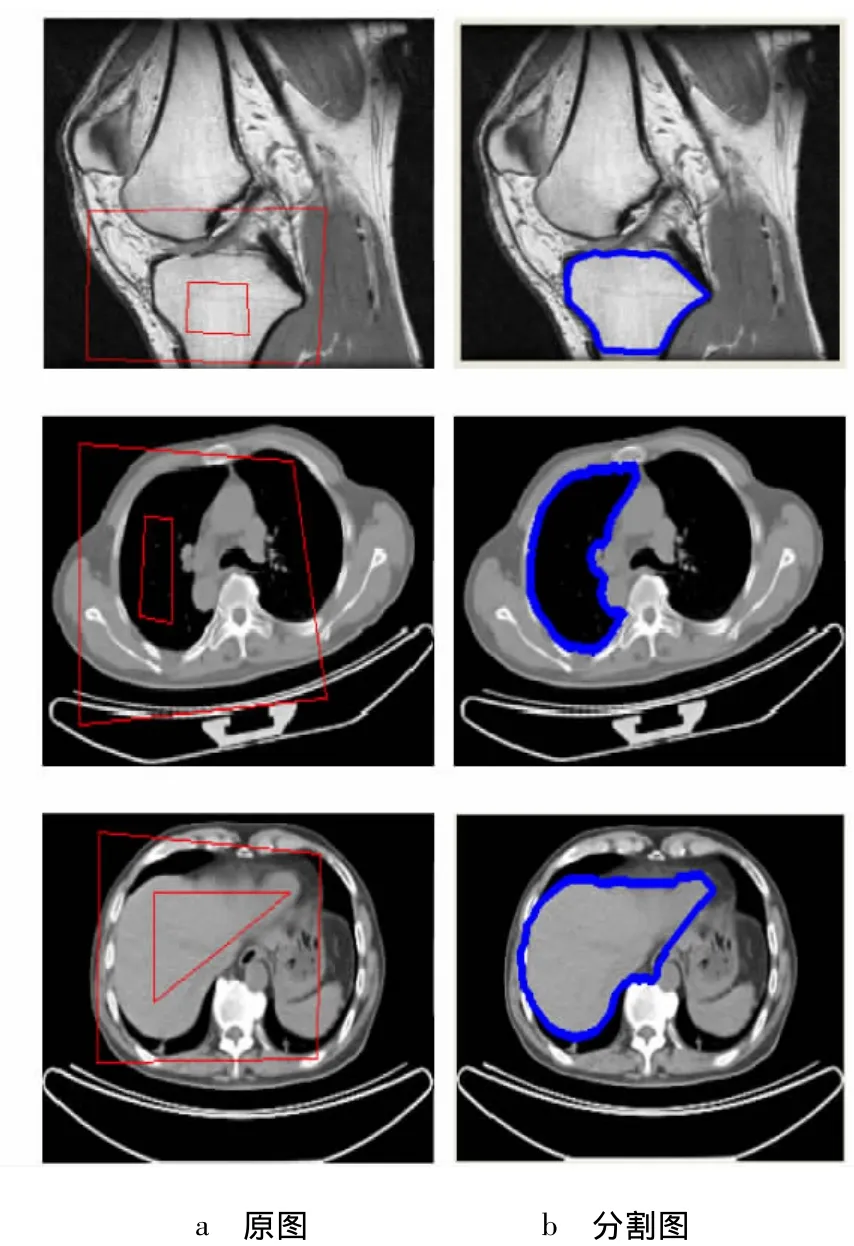
图11 本文算法分割效果图

图12 应用文献［7］算法的图像分割效果

表1 运行时间 s

3.2 三维分割

利用2.3部分的三维分割算法，可实现对CT序列图像的三维分割，如图13所示.先在第1张CT上交互的选择内外轮廓，如图13a所示.利用二维分割算法可以提取目标物体的轮廓，然后根据三维分割的算法，可以自动提取出目标物体在其它CT中的轮廓，如图13b所示.

由于CT在扫描时间距一般在0.5～5 mm之间，同一个目标物体的轮廓在2张CT之间相差不大.因此，在第1张CT的轮廓映射到第2张CT上的时候，已经最大限度的把第2张CT上的轮廓提取出来.在尽可能小的范围内提取目标物体轮廓，不仅轮廓效果提取的好，而且效率较高，从而实现整个肺部自动分割.

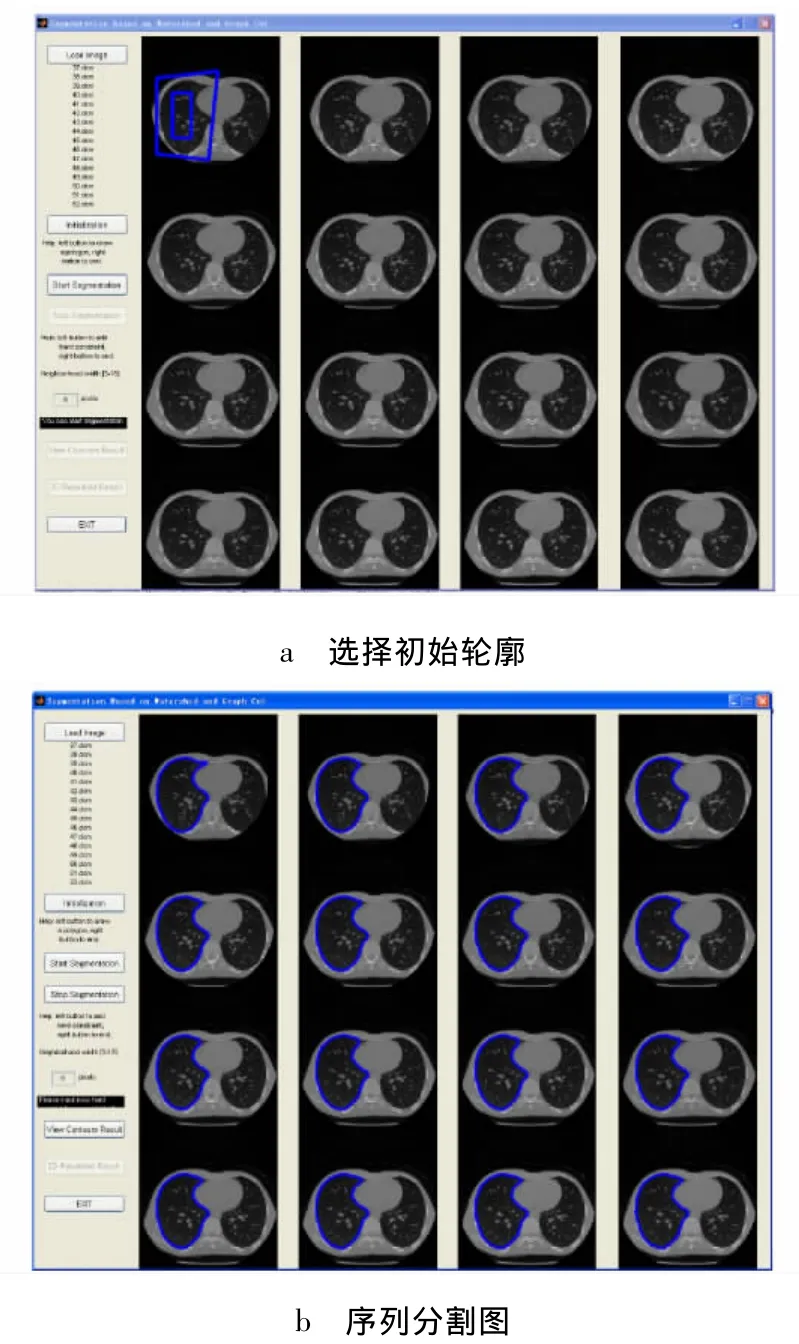
图13 三维分割

4 结论

本文把分水岭和图割结合起来，首先手动选择了内外轮廓，然后对内外轮廓部分进行预处理，最后应用最大流算法求最小能量.该算法能够达到比较准确的分割效果，同时还提高了运算效率.由于本文仍然是采用区域和边界相结合的方法，所以在分割效果上能够比较精确的得到目标物体的轮廓.运算效率通过以下几个方面得以提高:内外轮廓的选取缩小了查找范围，把预分割后的小区域作为一个像素点;把多源点和多汇点结构图转换成单源点和单汇点.然而，由于对细小的物体选择内外轮廓不太方便，因此本文算法对面积较大的物体提取效果较好，而对细小物体提取轮廓并不太好.

References)

［1］曹蕾，路利军，杨蕊梦，等.基于区域增长的肺结节自适应形态分割［J］.南方医科大学学报，2008，28(12):2109 －2125 Cao Lei，Lu Lijun，Yang Ruimeng，et al.Self-adapted segmentation of pulmonary nodule based on region growing［J］.J South Med Univ，2008，28(12):2109 －2125(in Chinese)

［2］赵锋，赵荣椿.分裂-合并方法在图象分割、目标提取中的应用［J］.西北工业大学学报，2000，18(1):116 －120 Zhao Feng，Zhao Rongchun.A new method for image segmentation［J］.Journal of North Western Polytechnical University，2000，18(1):116 －120(in Chinese)

［3］孔丁科，汪国昭.基于区域相似性的活动轮廓SAR图像分割［J］.计算机辅助设计与图形学学报，2010，22(9):1554－1560 Kong Dingke，Wang Guozhao.Region-similarity based active contour model for SAR image segmentation［J］.Journal of Computer-Aided Design ＆ Computer Graphics，2010，22(9):1554 －1560(in Chinese)

［4］Yuri Boykov，Gareth Funkalea.Graph cuts and efficient N-D image segmentation［J］.International Journal of Computer Vision，2006，70(2):109 －131

［5］Vincent L，Soille P.Watersheds in digital spaces:an efficient algorithm based on immersion simulation［J］.IEEE Transactions on Pattern Analysis and Machine Inteligence，1991，13:583 －598

［6］Li Yin，Sun Jian，Tang Chikeung，et al.Lazy snapping［J］.ACM Transactions on Graphics，2004，23(3):303 －308

［7］Xu Ning，Ahuja Narendra，Bansal Ravi.Object segmentation using graph cuts based active contours［J］.Computer Vision and Image Understanding，2007，107:210 －224

［8］Boykov Yuri，Kolmogorov Vladimir.An experimental comparison of min-cut max-flow algorithm of energy minimization in vision［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26(9):1124 －1137