等压和等容条件下的化学平衡原理
张志红 赵秀峰
(1,2.昌吉学院化学与应用化学系 新疆 昌吉831100)
等压和等容条件下的化学平衡原理
张志红1赵秀峰2
(1,2.昌吉学院化学与应用化学系 新疆 昌吉831100)
根据化学势不同的定义,分别讨论了等压和等容条件下的化学平衡原理。在一定温度和反应进度下,化学反应(ΔrGm)T,p=(ΔrAm)T,V,Δr=Δr。当没有其它功时,在一定温度和反应进度下,继续发生等压反应和等容反应的自发方向是一致的。根据对等温等压下化学反应的(ΔrGm)T,p的分析导出的一些化学平衡基本关系,如van’t Hoff等温方程以及,同样也适用于等容过程。
化学势;等压过程;等容过程;化学平衡
在没有其它功的前提下,Gibbs自由能G和Helmholtz自由能A分别是等温等压和等温等容条件下化学反应方向和平衡的判据。物理化学教科书常根据对等温等压条件下化学反应ΔrGm的讨论,导出化学反应van’t Hoff等温方程ΔrGm=ΔrGөm+RTlnQa;根据等温等压下化学平衡条件ΔrGm=0,导出ΔrGөm=-RTlnKө;利用Gibbs-Helmholtz公式,证明热力学平衡常数Kө与反应温度之间的关系,在此基础上讨论有关化学反应方向及化学平衡问题。其实,等容条件下的气相反应在工业中是很常见的,而教科书大都不涉及等容条件下化学反应方向及化学平衡的讨论。而在应用上述关系式讨论具体问题时,却又不要求等压的条件,例如,根据van’t Hoff等温方程讨论压力对气相化学平衡的影响;根据和计算等容反应(如刚性容器中的气相反应)的标准平衡常数Kө等[1-4],这给读者留下了一些疑问,有必要进一步剖析。
1 化学反应的(ΔrGm)T,p与(ΔrAm)T,V的关系
化学反应的等压热效应(ΔrHm)T,p与等容热效应(ΔrUm)T,V之间近似满足如下关系

所以,一般教科书只给出化合物的标准生成焓ΔfHөm或者标准燃烧焓ΔcHөm,由这些数据可以直接算出化学反应的ΔrHөm,根据上述(ΔrHm)T,p与(ΔrUm)T,V的关系,可以推算出化学反应的ΔrUөm。同样,教科书也只给出化合物的标准生成Gibbs自由能ΔfGөm数据,而没有标准生成Helmholtz自由能ΔfAөm数据。那么,化学反应的(ΔrGm)T,p和(ΔrAm)T,V之间是什么关系?

在无限大的反应系统中,(ΔrGm)T,p和(ΔrAm)T,V可以理解为状态函数G和A的变量。(ΔrGm)T,p的含义是,当反应进度为ξ时,维持ξ时的温度和压力,继续发生Δξ=1mol的反应所导致系统G的变化(系统的体积可能变化)。同理,(ΔrAm)T,V可以理解为,在反应进度为ξ时,维持ξ时的温度和体积,继续发生Δξ=1mol的反应所导致系统A的变化(系统的压力可能变化)。对于一个有限系统,(ΔrGm)T,p和(ΔrAm)T,V应该理解为反应进度为ξ时的状态函数,而不是状态函数的变量。(ΔrGm)T,p和(ΔrAm)T,V的意义是,在反应进度ξ的状态下,分别继续发生反应进度为dξ的微小等温等压和等温等容反应所导致G和A的微变。
在多组分系统中,任意组分B的化学势可以用G和A给出两个形式不同但数值相等的定义

在任意反应进度ξ时,化学反应的(ΔrGm)T,p和(ΔrAm)T,V分别定义为
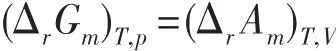
由于G和A的定义不同,(ΔrGm)T,p=(ΔrAm)T,V似乎不好理解。这里要注意,对于一个无限大系统,(ΔrGm)T,p和(ΔrAm)T,V分别对应于等温等压和等温等容两个不同的有限过程;对于一个有限系统,(ΔrGm)T,p和(ΔrAm)T,V分别对应于等温等压和等温等容两个不同的微小过程;因为对应的过程不同,(ΔrGm)T,p和(ΔrAm)T,V相等就可以理解了。
需要注意的是,对于一定温度下的化学反应,有
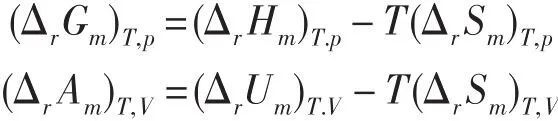
两式中的 (ΔrHm)T.p、(ΔrSm)T.p和 (ΔrUm)T.V、(ΔrSm)T.V也分别对应于不同的过程,若误认为(ΔrSm)T.p=(ΔrSm)T.V,由(ΔrHm)T.p和(ΔrUm)T.V的关系得出(ΔrGm)T,p=(ΔrAm)T,V+Δng(RT),这是不对的。

即,根据标准生成Gibbs自由能Δf计算得到的化学反应Δr,在数值上就等于相同温度下反应的Δr。
2 (ΔrGm)T,p、(ΔrAm)T,V与化学反应方向
在没有其它功时,(ΔrGm)T,p和(ΔrAm)T,V分别决定了等温等压和等温等容条件下化学反应的方向。对于化学反应,这意味着在某一反应状态(T,p,V,ξ,n1, n2...)下,维持ξ时的温度和压力继续发生反应的自发方向,与维持ξ时的温度和体积继续发生反应的自发方向是相同的;若在反应进度ξ时化学反应达平衡,系统的(ΔrGm)T,p和(ΔrAm)T,V同时等于零。
如前所述,化学势是系统的状态函数,其数值与化学势定义的形式无关,因此不论采用化学势定义或者,化学势的计算式μB=+RTlnaB都是成立的。因此,对于化学反应,根据,容易证明等温等压下,(ΔrGm)T,p=ΔrG+RTlnQa;同样地,根据,也可以证明等温等容下(ΔrAm)T,V=ΔrA+RTlnQa。
因为(ΔrGm)T,p=(ΔrAm)T,V,ΔrGөm=ΔrAөm,所以将van’t Hoff等温方程表示为

其中以符号ΔrGm代替(ΔrGm)T,p和(ΔrAm)T,V,以Δr代替Δr,表明在讨论化学反应方向和化学平衡问题时,van’t Hoff等温方程不再限定等压的条件(当然也不限定等容的条件)。因此,对于一定温度下的任意化学反应,不论反应是在等压条件还是等容条件下进行,反应的方向和平衡都可以根据van’t Hoff等温方程做出判断。
当反应达平衡时,(ΔrGm)T,p=(ΔrAm)T,V=0,因此

注意,Δr(或Δr)决定了标准平衡常数的大小,即决定了化学反应的限度,与化学反应的方向没有关系。若根据Δr或者Δr的正负,判断等温等压或者等温等容条件下化学反应的方向,这是没有理论依据的。Δr和Δr的数值只取决于对标准态的规定,与实际反应过程是等压还是等容没有关系,与实际反应系统的状态也没有关系。此外,Δr(或Δr对应的状态是反应物和产物各自处于标准态,而Kө对应的状态是反应物和产物处于化学平衡态,因此,上述关系表达的只是Δ(或Δr)与Kө数量之间的关系,并不对应于相同的状态。
3 热力学平衡常数Kө与温度的关系
多数教科书根据等温等压下化学平衡条件(ΔrGm)T,p=0,得出 Δr=-RTlnKө,然后根据Gibbs-Helmholtz公式,证明了等压条件下热力学平衡常数Kө与温度的关系,但又特别强调该式的成立与系统压力、以及系统是否等压无关[3],因此记作

因为不论是纯物质、气体还是溶液,其标准态都规定压力为Pө,因此Δr与系统的实际压力无关,相应地,Kө应当也与系统的压力无关,(1)式的成立应当不需要等压的条件。为进一步说明这一点,我们在等容条件下,采用化学势定义,证明(1)式仍然成立。
根据等温等容下化学平衡条件(ΔrAm)T,V=0,得出ΔrAөm=-RTlnKө。所以
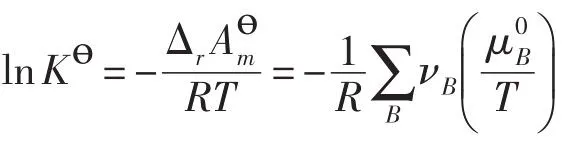


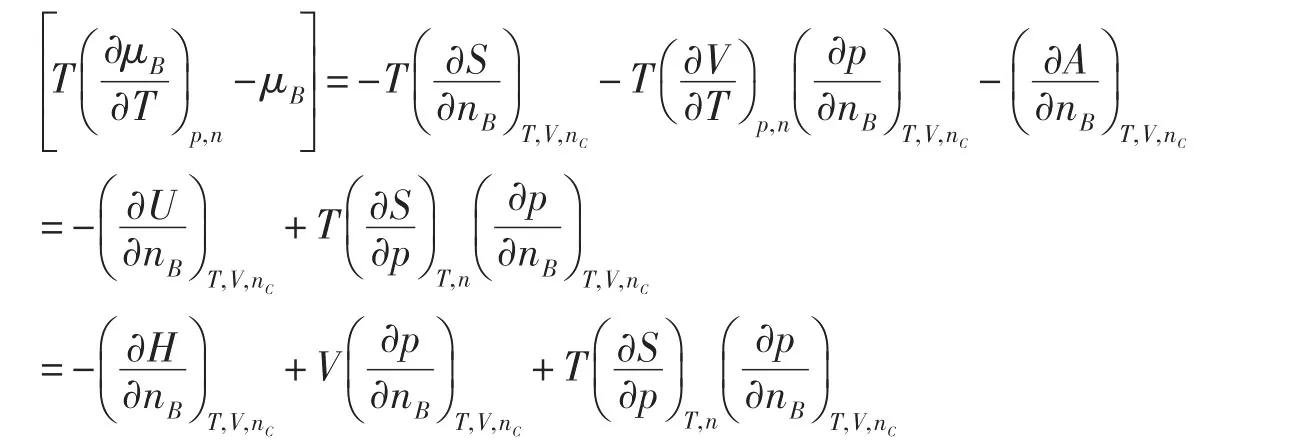
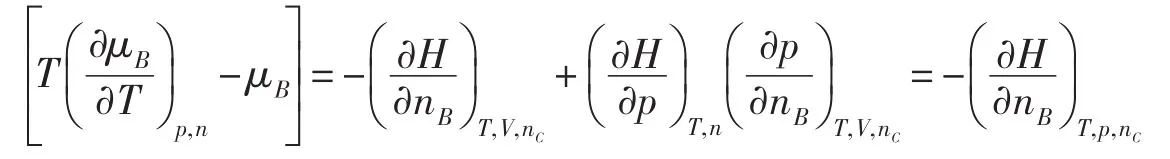
因此,在标准压力下,有

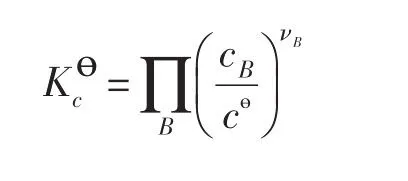
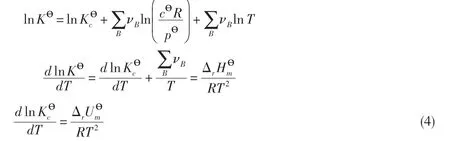
这里要强调,(1)式和(4)式在等压或者等容条件下都成立,有些基础化学教科书认为(1)式和(4)式分别表示的是等压和等容条件下标准平衡常数与温度之间的关系,这是不对的;其次,Kө和所对应的标准态的规定是不同的,因而对同一个化学平衡态,Kө和K数值也会不同;此外,所对应的标准态是pө=100kPa和cө=1mol⋅m-3,对于气体,满足这个条件的温度是唯一的。但是在应用(4)式讨论与温度之间的关系时,原则上要求气体在任何温度时都要同时满足 pө=100kPa和cө=1mol⋅m-3,实际上这是无法实现的,也就是说标准态是一种假想状态的气体,但这并不影响(4)式的成立。
综上所述,在一定温度和反应进度下,化学反应(ΔrGm)T,p=(ΔrAm)T,V,ΔrGөm=ΔrAөm。因此,当没有其它功时,在一定温度和反应进度的状态下,继续发生等压反应和等容反应的自发方向是一致的。根据等温等压下对化学反应(ΔrGm)T,p的讨论所导出的一些化学平衡基本关系,如van’t Hoff等温方程ΔrGm=ΔrGөm+RTlnQa、ΔrGөm=-RTlnKө以及,同样也适用于等容过程。
[1]傅献彩,沈文霞,姚天扬,侯文华.物理化学(第5版)[M].北京:高等教育出版社,2005:362-367.
[2]朱传征.物理化学[M].北京:高等教育出版社,2002:266-269.
[3]印永嘉,奚正楷,张树永.物理化学简明教程(第4版)[M].北京:高等教育出版社,2007:136-138,130.
[4]Peter Atkins,Julio de Paula.Atkins'Physical Chemistry:第7版.影印版[M].北京:高等教育出版社,2006:233-237.
O6-3
A
1671-6469(2012)04-0081-05
2012-08-12
昌吉学院2011年教学立项课题(11jyzd004)
张志红(1966-),女,昌吉学院化学与应用化学系,副教授,研究方向:无机化学教学与研究。

