道岔板孔位测量的数据处理与精度评估

何桂芳，刘民士

（滁州学院 地理信息与旅游学院，安徽 滁州239000）

道岔板是轨道结构的重要组成部分，也是轨道结构的薄弱环节之一，其加工质量决定着铁路运输系统的安全。为保证道岔板的制造精度，在其加工的关键工序—钻孔工序中，除需采用全站仪和电子水准仪进行精密测量控制外，还需对道岔板的孔位精度进行评估。

道岔板设计孔位数据是唯一的，而实测孔位数据受实际测量时地势以及道岔板和测量仪器摆放位置和方向的影响，导致实测数据和设计数据不一致，因此，在进行孔位精度评估时，需要先对实测孔位数据进行坐标转换，使其与设计孔位数据一致。为了建立实测数据和设计数据的坐标转换关系，通过道岔板中的3个边界孔位点来建立相对应的实测坐标系和设计坐标系，计算出这2个坐标系的转换关系，对实测数据进行坐标转换使其和设计数据的坐标系一致［1］。在得到转换后的实测数据后，通过横向较差、纵向较差和平整度3个方面对孔位精度进行评价。本文利用EXCEL强大的计算功能和函数功能，采用VBA编写程序扩展其功能，设计出一个相关的坐标转换程序，并通过程序设计实现孔位精度自动评估；同时利用EXCEL强大的绘图功能，通过折线图、XY散点图等，直观表达精度评估结果。

1 坐标变换的数学模型

由全站仪测量所得的实测孔位数据为三维坐标，设计数据采用二维平面坐标。为了便于转换，设计数据也采用三维坐标表示。如图1所示，黑色四边形表示水平放置的设计道岔板（其Z值均为0），蓝色四边形表示在任意倾斜面上放置的实际道岔板。实际道岔板必须先通过坐标变换与设计道岔板完全叠合在一起，才能评估实际道岔板的孔位精度。因此，需要建立一个坐标变换的数学模型。

1.1 构造坐标系

图1 设计道岔板与实际道岔板示意图

构造设计坐标系和实测坐标系：如图1所示，实际道岔板为O＊ABC，设计道岔板为OPQR。在设计道岔板OPQR中，选择靠左下角最近的孔位点作为原点O；选择靠近道岔板边沿、位于O的右侧、尽量远离O的那个孔位点P作为OX轴上的定向点，使得OX轴严格通过O、P；类似地，选出OY轴上的定向点S（它位于，或尽量接近Y轴）；最后，从O点开始作垂直向上的OZ轴，形成水平放置设计道岔板的三维坐标系OXYZ。同理，建立起实际道岔板对应的三维坐标系O＊X＊Y＊Z＊，通过3对关联点，建立相对应的设计坐标系和实测坐标系。

1.2 坐标系变换

坐标转换的物理意义就是通过平移、旋转和缩放，使2个刚体大小和形状完全相同［2］。

1）平移变换：将实测坐标系平移与设计坐标系原点重合，平移矢量（即O点坐标与O＊点坐标之差），平移后实测坐标系O＊X＊Y＊Z＊变换为OX′Y′Z′，如图2所示。

图2 实测坐标系平移变换示意图

2）旋转变换：2个同原点的任意三维坐标系要通过3次分别绕X轴、Y轴、Z轴旋转才能完全重合［3］，如图3所示：要将实测坐标系OX′Y′Z′与设计坐标系重合OXYZ，需依次将实测坐标系OX′Y′Z′围绕OY轴旋转角度α，使得OX′轴紧贴在水平面OPR上；围绕OZ轴旋转β角，使得OX′与OX轴严格重合；围绕OX轴旋转γ角，使得OY′与OY轴严格重合。求解出旋转角度α，β，γ，以α角度的求解为例：实测坐标系OX′Y′Z′围绕OY轴旋转角度α，即实际道岔板上各孔位点绕Y轴旋转α角。以A点为例，A点绕Y轴旋转α角后为L点，W 点（与L点重合）为A点在平面XOY投影，AL为A点在平面XOY上的投影AW，OL为OA在平面XOY上的投影OW ，于是可建立

式中：X′A，Y′A，Z′A分别为坐标系OX′Y′Z′下A 点X，Y，Z坐标，X′O，Y′O，Z′O分别为坐标系OX′Y′Z′下O点X，Y，Z坐标。故此，通过求解反正切即可求出角度α；同理可以求出另外2个旋转角度β，γ。

图3 实测坐标系旋转变换示意图

在实际程序设计时，为了简化旋转时的运算，可先将实测坐标系原点平移到（0，0，0），这样，式（1）OL的计算公式可简化为

旋转之后再将原点平移到设计坐标系原点。

1.3 误差纠正

理论上，经过变换后的实际道岔板应该和设计道岔板完全重合，但考虑到建立实测坐标系时选择参考点的测量误差，两者可能并不完全重合。例如，经过上述旋转变换后，因以X轴向点作为变换的参考点，因此Y轴可能不重合。如图4所示，此时，通过计算Y轴的偏转角度，对其逆方向旋转偏转角度的一半进行误差校正，达到减小误差的目的［4］。

图4 实际道岔板误差校正示意图

2 精度评估

在精度评估之前，需要对孔位数据进行匹配，找到和实测点相对应的理论设计点值，由于测量误差的存在，实测数据很难和相应的设计数据完全一致。本文采用按照实测点和设计点的最短距离，进行点匹配。匹配成功后，对实测点和设计点之间进行较差。通过横向较差、纵向较差、平整度3个方面进行精度评估。

2.1 横向较差

假定在设计道岔板与实际道岔板上各有n个孔位，在设计道岔板上某个孔位点坐标为（Xi，Yi，0），此时在实际道岔板上，对应点坐标为，经过变换及误差纠正后其对应点的坐标为求各孔位点横向误差的计算公式为

由于道岔板整体平移不影响其精度。故可以对横向直接较差值进行优化，即在直接较差的基础上加上直接较差平均值，得到其优化后较差。验收道岔板要求ΔXi在0.5mm以内［5］。故横向合格率等于优化较差在0.5mm以内的孔位点的个数与孔位点总数的比值。

2.2 纵向较差

同理，求得各孔位点纵向误差的公式为

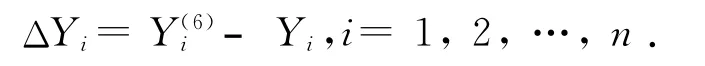
同理，先求得直接较差再进行优化，验收道岔板要求ΔYi在0.5mm以内。故纵向合格率等于纵向优化较差在0.5mm以内的孔位点的个数与孔位点总数的比值。

2.3 平整度

加工或者生产道岔板时，表面并不绝对平整，道岔板上孔位点的实测水平数据与设计水平之间所差数值，就是平整度。道岔板的几何尺寸值中平整度越小越好。平整度将直接影响钢轨的平整程度，也就是说影响着后续的列车运行平稳性、舒适性及安全性［6］。

ΔZi反映道岔板的平整度，要求控制在2mm以内，可用EXCEL做出各点ΔZi的折线图，直观反映道岔板的平整度。

3 算 例

选取一块18号道岔板的设计值和实测值为例，对测量数据进行格式转换后，保存为CSV格式，在EXCEL中打开，如表1所示。

表1 实验原始数据表 m

1）构建坐标系：通过计算 min（X＋Y）、max（X-Y）、max（Y-X），分别求得设计道岔板的原点为20601号，X轴点为20605号，Y轴点为20602号。根据散点图（见图5、图6）相应的位置确定实测道岔板的原点为30601号，X＊轴点为30603号，Y＊轴点为30606号。

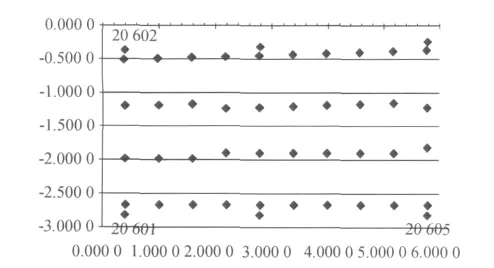
图5 设计点散点图

图6 实测点散点图

2）坐标变换：为方便计算，先将坐标系平移至原点（0，0，0），然后旋转，使实测坐标系与设计坐标系共面。最后通过一次平移和旋转使2个坐标系统一。根据原点和X轴向点计算平移和三个旋转角度：平移分量 （-0.479 8，18.636 8，-10.300 2），绕Z轴旋转角度β＝0.006 4°，绕Y 轴旋转角度α＝298.132 1°，绕X 轴旋转角度γ＝359.965 0°；统一坐标系的平移分量 （0.393 0，-2.813 7），旋转角度为0.012 1°。各点转换后坐标如表2所示。

表2 坐标变换数据表 m

3）误差纠正：根据求取设计坐标与实测坐标的Y轴夹角，进行误差纠正，求得旋转角度为-0.017 2°。结果见表3。

4）精度评估：根据设计数据和转换后的数据进行直接较差，并对横纵向的直接较差进行优化。结果如表3所示。

使用EXCEL公式计算各指标如表4所示。

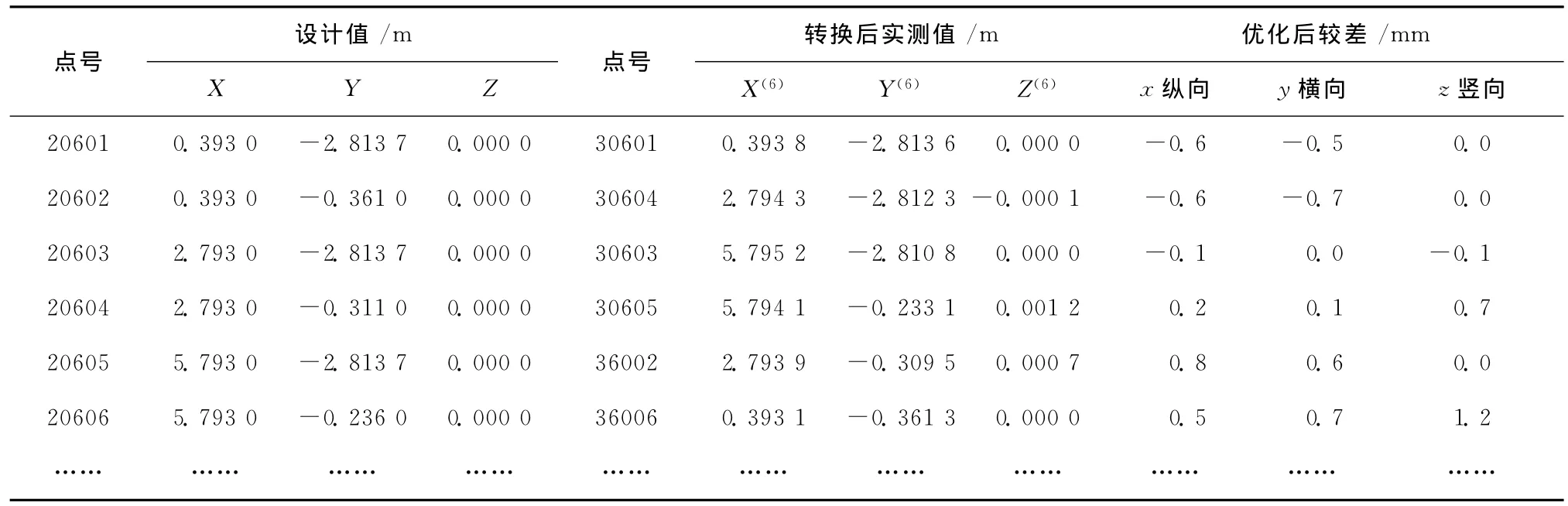
表3 实验结果数据表

表4 精度评估小结表

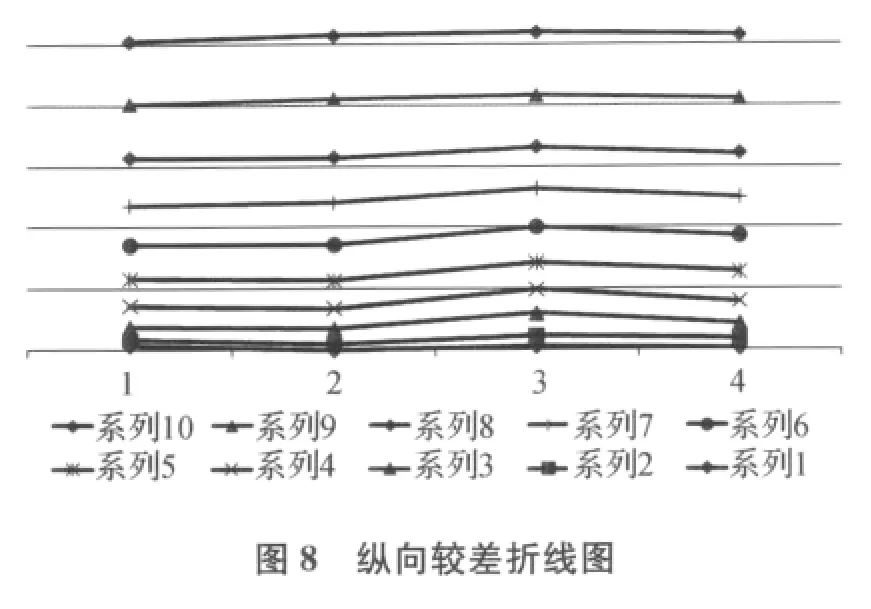
从图5可以看出，除去棱镜点和其他点，该道岔板有40个扣件点。故分析横向较差时，沿X轴方向看，可将数据分为4个序列，按照Y值对数据进行排序，如图7所示。同理，分析纵向较差时，沿Y轴方向分析，按照X值对数据排序，可将数据分成10个序列，如图8所示。对平整度的分析，按照X轴方向将数据分为4个序列，如图9所示。

从评估结果可以看出，该道岔板横纵向较差都比较均衡，基本符合要求。从平整度来看，虽然各点平整度都小于2mm，但第一系列的点平整度较小，其他3列的点平整度相对较大，反应出该板测量时是倾斜的。

4 结束语

本文对道岔板孔位测量精度进行评估，为了能够真实的评估，本文提出一种将实测点变换到理论点的变换方法，之后根据实际精度要求，从横向较差，纵向较差，平整度3个方面对孔位精度进行评估，最后通过一个实例进行验证。实验证明，本方法方便且有效。

［1］冀光民，吕文超，宋剑.道岔板铺设精密测量技术［J］.铁道标准设计，2010（1）：86-89.

［2］姚吉利.3维坐标转换参数直接计算的严密公式［J］.测绘通报，2006（5）：7-10.

［3］同济大学数学系.高等数学［M ］.北京：高等教育出版社，2007.

［4］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉：武汉大学出版社，2009.

［5］铁道部运输局.客运专线铁路岔区板式无砟轨道混凝土道岔板检验细则［J］.铁道技术监督，2009，7（37）：59-63.

［6］陈兴，范叹奇.高速铁路CRTSII型轨道板几何尺寸检测技术及方法［J］.铁道勘察，2010（2）：8-10.