喷射成形FGH95高温变形流变应力行为与预测

郭 彪，葛昌纯,，徐 轶，张 宇，孙传水

(1.西南交通大学 材料科学与工程学院，成都 610031；2.北京科技大学 材料科学与工程学院 特种陶瓷粉末冶金研究所，北京 100083)

FGH95是高合金化的γ′相沉淀强化型镍基高温合金，具有良好的耐高温和抗蠕变性能，主要用于航空发动机的涡轮盘、轴和压气机盘等重要部件，国外近似牌号Rene95[1-3]。由于高温合金粉末易受污染，热等静压过程中粉末颗粒表面易产生碳偏析，所制备的粉末高温合金材料含有较多的粉末原始颗粒边界(PPB)，降低材料的高温拉伸、持久断裂和低周疲劳性能[3-4]。而采用喷射成形工艺可制备与粉末冶金相似的无宏观偏析且晶粒细小均匀的组织，同时避免粉末冶金中易出现的PPB，节省工序和成本[5-7]。但是，FGH95合金热加工变形抗力大，变形温度高且温度窗口窄，热加工工艺条件对FGH95合金变形行为有显著影响。因此，研究喷射成形FGH95合金热变形行为，建立流变应力本构方程对深入了解其变形规律具有重要意义。

材料高温变形本构关系是指材料热变形时流变应力与变形程度、变形温度和应变速率之间的依赖关系。人们通常采用 JONAS等[8]提出的双曲正弦修正的Arrhenius方程来描述材料本构关系[9-11]，或在其基础上进行改进[12]。LIU等[10]研究了 FGH96合金的热变形行为，得到FGH96的峰值流变应力本构方程，发现应变速率大于0.002 s-1时，动态再结晶是合金高温软化的主导机制。OKTAY ALNIAK 和 BEDIR[13]及ZHANG等[12]在研究 Rene95合金热变形行为的基础上，模拟了 Rene95的等温锻造过程，为热加工工艺提了理论依据。KANG等[11,14]研究了喷射成形+热等静压高温合金的热变形行为，建立了合金的峰值流变应力本构方程，并结合热加工图提出了优化的热加工工艺。另外，也有一些学者利用正交回归[15]、多元非线性回归[16]和神经网络[17]等纯数学方法建立材料的本构关系，但未能体现金属热变形过程受热激活能控制的物理特征。目前，关于喷射成形FGH95合金热变形流变应力行为的研究还未见报道。因此，本文作者基于喷射成形FGH95合金在变形温度1 050～1 140 ℃和应变速率0.01～10 s-1条件下的高温热压缩实验，采用双曲正弦修正的Arrhenius方程，以最小二乘法拟合的四次多项式函数考虑累积应变量对流变应力的影响，建立改进的喷射成形FGH95合金的本构方程。最后对建立的本构方程进行了验证。

1 实验

实验用FGH95合金的化学成分(质量分数，%)为：C 0.04～0.09，Mo 3.30～3.70，Al 3.30～3.70，W 3.30～3.70，Nb 3.30～3.70，Cr 12.0～14.0，Co 7.0～9.0，Ti 2.30～2.70，Mn≤0.15，S≤0.015，P≤0.015，O≤0.015，Ni余量。经氩气保护熔炼雾化后的喷射成形态组织平均晶粒尺寸约为23 μm，如图1所示。沿喷射沉积方向线切割d8 mm×12 mm圆柱形热压缩试样。在Gleeble-1500热模拟机上进行高温热压缩实验，试样上下端面与压头间垫石墨片减少摩擦对应力状态影响，通过自动测控系统在预设的温度和应变速率下进行恒温、恒应变速率压缩。试样热压缩前以 10 ℃/s升温速率分别升温到1 050、1 080、1 100和1 140 ℃，保温3 min后分别以0.01、0.1、1.0和10 s-1应变速率压缩50%，同时记录应力—应变曲线。

图1 喷射成形FGH95原始晶粒形貌Fig.1 Morphology of original grains of spray-forming FGH95

2 结果与分析

喷射成形 FGH95合金在不同变形条件下的真应力—真应变曲线，具有典型的动态再结晶特征，如图2所示。在实验范围内合金的流变应力变化趋势是：在初始变形阶段，由于大量位错的增殖和积累，位错间的交互作用阻碍位错进一步运动，合金变形抗力随应变增加迅速增大，此时加工硬化率大于软化率；随着应变量增大，位错密度不断增高，在晶体内部储存能的驱动下产生的动态回复和部分动态再结晶软化抵消了部分加工硬化，使合金的加工硬化率减小，当软化作用和硬化作用相等时，流变应力曲线达到峰值；随着变形量继续增大，动态再结晶软化作用超过了加工硬化，使流变应力随应变增加而降低；最后加工硬化与动态再结晶软化趋于动态平衡时，流变应力即进入稳态流变阶段。喷射成形FGH95合金在较高温度和较低应变速率下变形时(如变形温度为1 140 ℃，应变速率为0.01 s-1)，应力应变曲线过渡阶段窄小，且出现了稳态流变特征；在较低温度和高应变速率下变形时，流变应力峰较宽大，且具有明显的软化特征。而较高的温度和应变速率均加快了合金动态再结晶的发生。

图2 喷射成形FGH95不同应变速率和温度下的真应力—真应变曲线Fig.2 True stress—true strain curves of spray-forming FGH95 at different strain rates and temperatures: (a)1 050 ℃; (b)1 080 ℃;(c)1 100 ℃; (d)1 140 ℃

另外，当变形温度一定时，合金流变应力随应变速率增大而升高。这主要是由于应变速率增加，单位时间内产生的位错密度增加，位错运动受阻，位错攀移及位错反应等引起的软化速率相对降低，使得合金硬化增强，临界切应力升高，最终导致流变应力增大。同时，合金变形时间缩短，单位时间内动态再结晶的形核数目减少，软化程度下降，间接地也使合金的流变应力增大。而在应变速率一定时，合金流变应力随温度的升高而降低。这主要是因为随着变形温度升高，合金中原子的热激活作用加剧，位错的活动能力增强，更多的位错进行交滑移和攀移，从而使软化过程更为突出，流变应力下降[18]。同时，合金动态再结晶的形核率和长大速率也随温度的升高而增加, 使动态再结晶软化作用增强, 导致流变应力降低[19]。

分别作喷射成形 FGH95合金热变形过程中不同条件下的峰值应力、峰值应变与变形温度、应变速率之间的关系曲线如图3(a)～(c)所示。在一定的应变速率下合金峰值应力随温度的升高成线性降低；而在一定的温度下合金峰值应力随应变速率的增大成指数增加。这说明合金流变应力对应变速率和变形温度非常敏感，且受应变速率的影响远高于温度，因此，合金热加工过程中应准确控制这两个因素。如图3(c)所示，合金在0.1～10 s-1应变速率范围内变形时，峰值应变随温度升高而降低，在1 080 ℃以上趋于平稳；但当应变速率为0.01 s-1时，合金峰值应变出现了较大波动，在1 100 ℃发生突变，达到极大值。为降低喷射成形FGH95合金热加工时的成形力和模具负荷，可在应变速率低于0.1 s-1和温度高于1 050 ℃条件下进行热加工。考虑合金动态再结晶发生的难易程度，喷射成形FGH95合金热成形应变速率为0.01 s-1时，应避免在1 100 ℃下进行。

3 喷射成形FGH95合金本构方程

3.1 本构方程的建立

图3 喷射成形FGH95峰值应力与温度和应变速率、峰值应变与温度的关系曲线Fig.3 Relationship curves of peak stress—temperature (a),peak stress— ln ˙ (b)and peak strain—temperature (c)

从喷射成形 FGH95合金的高温流变应力曲线分析可知，合金流变应力强烈地取决于变形温度和应变速率，并在整个变形过程中形成应变硬化和动态软化的动态平衡。合金流变应力、变形温度和应变速率三者之间的关系可用Arrhenius方程表示[8]，而变形温度和应变速率对合金变形行为的影响可用Zener-Hollomon参数Z表示，物理意义为温度补偿的应变速率因子[20]。

式中：为应变速率，s-1；R为摩尔气体常数，8.314 J/(mol·K-1)；T为热力学温度，K，Q为热变形激活能，J/mol；σ为一定应变时的流变应力，MPa；A、α、n、n1和β均为与温度无关的常数，α=β/n1。

研究结果[21-22]表明采用双曲正弦修正的Arrhenius方程(5)能更好地描述材料的常规热变形过程，且在不同应力条件下可简化为式(3)和(4)。但式(5)仅表示某一应变量下，流变应力与变形温度和应变速率之间的关系，而合金实际变形过程中，流变应力除了受变形温度和应变速率影响，还随应变增加而变化。未考虑应变量影响的本构方程对材料热变形流变应力的预测误差是比较大的，甚至是无法接受的。因此，考虑累积应变量对材料组织演变和变形状态的影响，本研究将A、α、n、β和Q等材料常数视为应变的函数，计算不同应变量(ε为0.05～0.65，间隔量为0.025)下的材料常数并进行回归拟合，建立改进的喷射成形FGH95合金的本构方程。

3.2 材料参数的确定

在低应力水平和高应力水平下，分别将式(3)和(4)代入式(2)，并对两边取对数后整理可得

取不同真应变ε及对应真应力σ，分别作ln˙—lnσ和lnε˙—σ关系曲线，并采用最小二乘法线性回归求得所取应变量下的平均n1和β，进而确定α与真应变ε的关系。图4所示为ε=0.2时的实验数据和回归结果。

将式(5)代入式(2)两边取对数可得

对式(7)求偏微分可得热变形激活能Q为

取不同真应变ε，分别在一定温度T和应变速率ε下，作ln—ln[sinh(ασ)]和 ln[sinh(ασ)]—T-1关系曲线，并分别采用最小二乘法线性回归求得所取应变量下的平均斜率n和k，进而确定喷射成形FGH95合金热变形激活能Q与真应变ε的关系。图5所示为ε=0.2时ln—ln[sinh(ασ)]和 ln[sinh(ασ)]—T-1实验数据和回归结果。

图4 不同温度下的流变应力—应变速率的关系曲线Fig.4 Relationship curves of lnε— lnσ (a)and lnε—σ(b)at different temperatures (ε=0.2)

由式(1)求得一定应变量时不同条件下的Z，并对式(1)两边取对数得

取不同真应变ε及对应真应力σ，作 lnZ—ln[sinh(ασ)]关系曲线，并采用最小二乘法线性回归求得所取应变量下的n和lnA，将n值代入式(8)可求出更精确Q值。图6所示为ε=0.2时 lnZ—ln[sinh(ασ)]实验计算值和回归结果，拟合相关系数为0.995 33。

分别以不同真应变下的α、Q、n和lnA参数为函数，真应变ε为自变量进行四次多项式回归，得到图7所示拟合曲线和拟合相关系数，可见材料参数与真应变ε的四次多项式拟合较好。

根据拟合结果，结合式(1)、(2)和(5)可得喷射成形

图5 不同温度下的lnε—ln[sinh(ασ)]和不同应变速率下的ln[sinh(ασ)]—T-1关系曲线Fig.5 Relationship curves of lnε—ln[sinh(ασ)]at different temperatures (a)and ln[sinh(ασ)]—T-1 at different strain rates(b)(ε=0.2)

图6 喷射成形FGH95合金热变形Z参数—流变应力关系Fig.6 Relationship between lnZ—ln[sinh(ασ)]of sprayforming FGH95 alloy

图7 材料参数和应变量的关系Fig.7 Relationships between material parameters and strain: (a)α—ε; (b)Q—ε; (c)n—ε; (d)lnA—ε

FGH95合金高温变形本构模型：

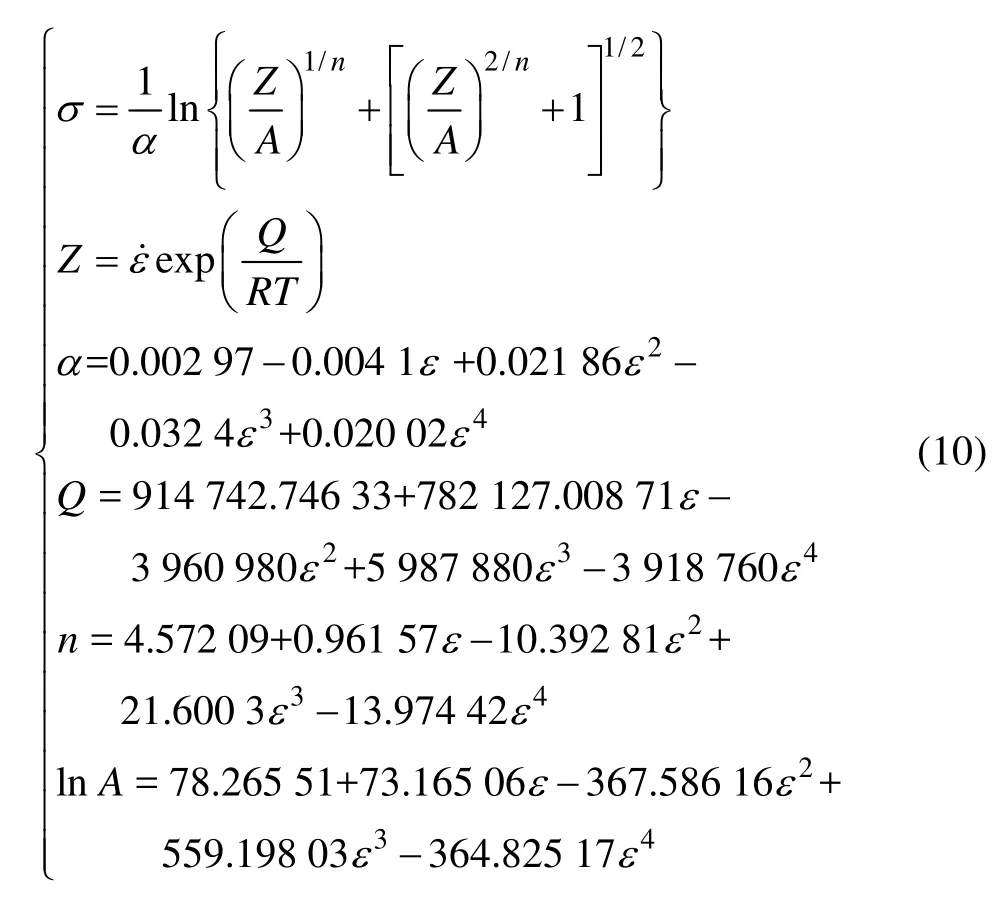
3.3 本构模型的验证

为了验证不同变形温度、应变速率和应变量下本构模型预测流变应力的准确性，将由本构模型(10)计算出的流变应力预测值与实验值进行了对比，预测值与对应实验值吻合较好(见图8)。

为了更加准确地检验本构方程的精确度，引入相关系数R和平均相对误差AARE[22]

式中：E为实验值，P为预测值，E0和P0分别为E和P的平均值，N为分析的数据点个数。相关系数R通常用来分析实验值和预测值间线性关系的强弱，但不一定能代表数据间的符合性，因为相关系数高时，预测值也有可能全部偏高或偏低[23]。而平均相对误差AARE对本构关系模型的可预测性的分析是无偏差的。因此结合R和AARE可验证本构关系模型预测的精确度。

图8 不同应变速率和温度下本构关系模型预测的流变应力与实验值对比Fig.8 Comparison between experimental and predicted flow stress from constitutive equation at different strain rates and temperatures: (a)1 050 ℃; (b)1 080 ℃; (c)1 100 ℃; (d)1 140 ℃

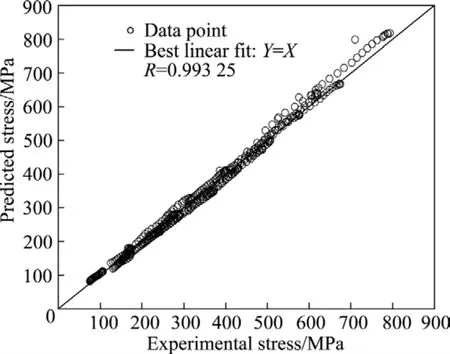
图9 本构模型预测流变应力值与实验值的相关性Fig.9 Correlations between experimental and predicted flow stress data from constitutive equation

图9所示为本构模型预测的流变应力与实验值的相关性，相关系数R为0.993 25，预测值与实验值相关性较好。计算全部400组预测值与实验值的相对误差分布如图10所示，除极个别点外，相对误差均小于10%，平均相对误差ARRE为3.64%，综合R和ARRE说明所建立的本构方程具有良好的预测能力。

图10 本构模型预测流变应力值与实验值相对误差分布Fig.10 Relative error distribution between experimental and predicted flow stress data from constitutive equation

4 结论

1)喷射成形FGH95合金在实验条件范围内高温压缩变形过程中，流变应力受变形温度和应变速率影响强烈，当应变速率一定时，合金峰值应力随变形温度的升高成线性降低；当变形温度一定时，合金峰值应力随应变速率的增大而成指数增加。合金在热变形初期，流变应力随应变增加迅速达到峰值，随后呈现动态软化特征。

2)喷射成形FGH95合金高温压缩变形时峰值应变在应变速率大于0.01 s-1时，随温度升高而减小，并趋于平稳；而应变速率为0.01 s-1时，出现了较大波动，并在1 100 ℃时达到极大值，应避免在此温度和应变速率下进行热加工。

3)建立了考虑应变量影响的喷射成形FGH95的高温变形本构方程，材料常数(α、Q、n和lnA)可用包含应变量的四次多项式函数表达；改进的本构方程流变应力预测值与实验值的相关系数为0.993 25，平均相对误差为 3.64%，较好地反映了合金在热变形过程中流变应力的变化规律。

[1]李红宇, 宋西平, 王艳丽, 陈国良.FGH95合金中γ′相稳定性研究[J].稀有金属材料与工程, 2009, 38(1): 64-67.LI Hong-yu, SONG Xi-ping, WANG Yan-li, CHEN Guo-Liang.Stability ofγ′ phase in FGH95 superalloy[J].Rare Metal Materials and Engineering, 2009, 38(1): 64-67.

[2]郭建亭.高温合金材料学(下册)：高温合金材料与工程应用[M].北京: 科学出版社, 2010: 251-262.GUO Jian-ting.Materials science and engineering for superalloy(2vols): Superalloy materials and engineering applications[M].Beijing: Science press, 2010: 251-262.

[3]TAO Yu, JIA Jian, LIU Jian-tao.Microstructure characterization and mechanical properties of FGH 95 turbine blade retainers[J].Journal of Iron and Steel Research International, 2010, 17(9):73-78.

[4]RAO A G, SRINIVAS M, SARMA D S.Effect of thermomechanical working on the microstructure and mechanical properties of hot isostatically pressed superalloy Inconel 718[J].Materials Science and Engineering A, 2004,383(2): 201-212.

[5]ZHANG Jing-guo, SHI Hai-sheng, SUN De-sheng.Research in spray forming technology and its applications in metallurgy[J].Journal of Materials Processing Technology, 2003, 138(1/3):357-360.

[6]张国庆, 李 周, 田世藩, 颜鸣皋.喷射成形高温合金及其制备技术[J].航空材料学报, 2006, 26(3): 258-264.ZHANG Guo-qing, LI Zhou, TIAN Shi-fan, YAN Ming-gao.Spray formed superalloys and their fabrication technologies[J].Journal of Aeronautical Materials, 2006, 26(3): 258-264.

[7]陈振华, 严红革, 陈 刚, 张福全, 胡仲勋, 傅杰新.多层喷射沉积的装置和原理[J].湖南大学学报: 自然科学版, 2001,28(5): 20-28.CHEN Zhen-hua, YAN Hong-ge, CHEN Gang, ZHANG Fu-quan, HU Zhong-xun, FU Jie-xin.Principle and setups of multi-layer spray deposition technology[J].Journal of Hunan University: Natural Science, 2001, 28(5): 20-28.

[8]JONAS J J, SELLARS C M, TEGART W J McG.Strength and structure under hot working conditions[J].International Materials Reviews, 1969, 14: 1-24.

[9]THOMAS A, El-WAHABI M, CABRERA J M, PRADO J M.High temperature deformation of Inconel 718[J].Journal of Materials Processing Technology, 2006, 177(1/3): 469-472.

[10]LIU Jian-tao, LIU Guo-quan, HU Ben-hu, SONG Yue-peng,QIN Zi-ran, ZHANG Yi-wen.Hot deformation behavior of FGH96 superalloys[J].Journal of University of Science and Technology Bejing, 2006, 13(4): 319-323.

[11]KANG Fu-wei, ZHANG Guo-qing, SUN Jian-fei, LI Zhou,SHEN Jun.Hot deformation behavior of a spray formed superalloy[J].Journal of Materials Processing Technology, 2008,204(1/3): 147-151.

[12]ZHANG Mai-cang, DONG Jian-xin, ZENG Yan-ping, XIE Xi-shan.A phenomenological constitutive equation for Rene 95 PM alloy and its application to isothermal forging process of turbine disk[J].Journal of University of Science and Technology Beijing, 2002, 9(4): 282-286.

[13]OKTAY ALNIAK M, BEDIR F.Modelling of deformation and microstructural changes in P/M Rene 95 under isothermal forging conditions[J].Materials Science and Engineering A,2006, 429(1/2): 295-303.

[14]KANG Fu-wei, ZHANG Guo-qing, LI Zhou, SUN Jian-fei.Hot deformation of spray formed nickel-base superalloy using processing maps[J].Transactions of Nonferrous Metals Society of China, 2008, 18(3): 531-535.

[15]侯红亮, 姜 波, 王耀奇, 李志强, 任学平.基于正交回归的GH44合金本构关系研究[J].锻压技术, 2005(1): 61-63.HOU Hong-liang, JIANG Bo, WANG Yao-qi, LI Zhi-qiang,REN Xue-ping.Research on constitutive equation of GH44 nickel base alloy based on orthogonal regression[J].Forging &Stamping Technology, 2005(1): 61-63.

[16]张麦仓, 罗子健, 曾凡昌.应用多元非线性回归方法建立FGH95合金的本构关系[J].材料工程, 1999(1): 20-24.ZHANG Mai-cang, LUO Zi-jian, ZENG Fan-chang.Establishment of constitutive relationship for FGH95 alloy using multiple nonlinear regression method[J].Journal of Materials Engineering, 1999(1): 20-24.

[17]孙 宇, 曾卫东, 赵永庆, 戚运莲, 韩远飞, 邵一涛, 马 雄.基于BP神经网络Ti600合金本构关系模型的建立[J].稀有金属材料与工程, 2011, 40(2): 220-224.SUN Yu, ZENG Wei-dong, ZHAO Yong-qing, QI Yun-lian,HAN Yuan-fei, SHAO Yi-tao, MA Xiong.Modeling of constitutive relationship of Ti600 alloy using BP artificial neural network[J].Rare Metal Materials and Engineering, 2011, 40(2):220-224.

[18]潘金生, 仝健民, 田民波.材料科学基础[M].北京:清华大学出版社, 2011: 540-545.PAN Jin-sheng, TONG Jian-min, TIAN Min-bo.Fundamentals of materials science[M].Beijing: Tsinghua University Press,2011: 540-545.

[19]DEBORAH A D.Recovery and recrystallization in nickel based superalloys[D].Virginia: University of Virginia, 2002.

[20]ZENER C, HOLLOMON J H.Effect of strain rate upon plastic flow of steel[J].Journal of Applied Physics, 1944, 15(1): 22-32.

[21]MCQUEEN H J, RYAN N D.Constitutive analysis in hot working[J].Materials Science and Engineering A, 2002,322(1/2): 43-63.

[22]SAMANTARAY D, MANDAL S, BHADURI A K.A comparative study on Johnson Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr-1Mo steel[J].Computational Materials Science, 2009, 47(2):568-576.

[23]PHANIRAJ M P, LAHIRI A K.The applicability of neural network model to predict flow stress for carbon steels[J].Journal of Materials Processing Technology, 2003, 141(2): 219-227.