Analysis on Fracture Toughness Test Results of Candidate Titanium Alloys Used in Deep Manned Submersibles
WANG Fang,CUI Wei-cheng,SHEN Yun-sheng,PAN Bin-bin
(China Ship Scientific Research Center,Wuxi 214082,China)
1 Introduction
The manned pressure hull of submersibles provides a safe living space for pilots and scientists,which should be designed to have enough strength and should be as light as possible.The current material selection and design rules for the spherical pressure hull of manned submersibles pay more attention to the synthetic properties of materials of interest for high safety and reliability.Damage-tolerant properties will be considered for more optimized design principle in the future.Titanium alloys with relatively high ductility,maturity,welding properties and corrosion resistance are widely used in the existing pressure hulls of submersibles.Several types of titanium alloys are developed for this purpose.Fracture toughness and fatigue crack growth rate are the two main damage-tolerant properties.For the material selection and design of a 4 500 m depth manned submersible in China,fracture toughness testing is conducted on two types of candidate titanium alloys of interest(Ti80 and TC4 ELI)for the pressure hull.
Many standards can be employed in test design such as ASTM Std.E399[1]and its improved version ASTM Std.E399-09ε2[2]which specify the plain strain fracture toughness,KIC, testing procedure.Some restrictions governed by linear elastic fracture mechanics(LEFM)should be satisfied.The size criteria in ASTM Std.E399[1]have been used in KICtests for many years[3]though they are now facing questions by many researchers[4-5]on whether they are oversize or inadequate.In ASTM Std.E399-09ε2[2],the specimen size criterion was relaxed.However,the standard specimen size in section 2 is still designed according to the size criterion in ASTM Std.E399[1].
The specimen size is required to ensure predominately linear-elastic,plane-strain conditions.And a range of proportional specimens is recommended in standards.But when relatively ductile materials are tested,very large specimen may be necessary for test validity.The experiments for this purpose are costly from the engineering viewpoint.Then some researchers[6]have proposed a three dimensional fracture criterion to consider the effect of stress state on fracture toughness of materials.By proper analysis,the test results by small size specimens or non-standard specimens may be enough to obtain correct value.The interaction of large scale yielding with specimen size effects when testing ductile materials must be paid attention.Quite different degree of plastic deformation will bring varieties of micro fracture mechanics and macro fracture mode.Furthermore,the plain-strain fracture toughness KICmay be too conservative for the structure to be designed with small thickness,and non-standard specimens are more applicable.Then more applicable and cheap non-standard specimens can be designed for engineering purpose but the reliability of the test results must be validated.
In this paper,test results from series non-standard specimens are presented.Thickness effect is specifically investigated using specimens with similar ligament size.Analysis on the tendency of KQand Pmax/PQdata of Ti80 and TC4 ELI with increasing specimen thickness will be conducted.
2 Experiments
Sets of KCcompact-tension(C-T)specimens of different thickness are machined out from spherical base material of the pressure hull made of candidate titanium alloys,Ti80 and TC4 ELI.Ti80 is a near α-type alloy with nominal composition of Ti-6A1-2Zr-lMo-3N[7].TC4 ELI is a beta-annealed Ti-6Al-4V(extra-low interstitials,ELI).Each set contains at least five specimens of different thickness including 10 mm,20 mm,30 mm,40 mm and 50 mm,and Fig.1 shows other dimensions of the specimens.Among them,the specimen with thickness of 50 mm is designed according to the American standard ASTM E399[1]with W/B=2 while others are designed to be non-standard with the same width,W,to eliminate ligament effect.Pre-fatigue cracking procedure is conducted to obtain similar initial crack,a,before the test.The crack mouth opening displacement against loading curve is recorded for determination of KQ.
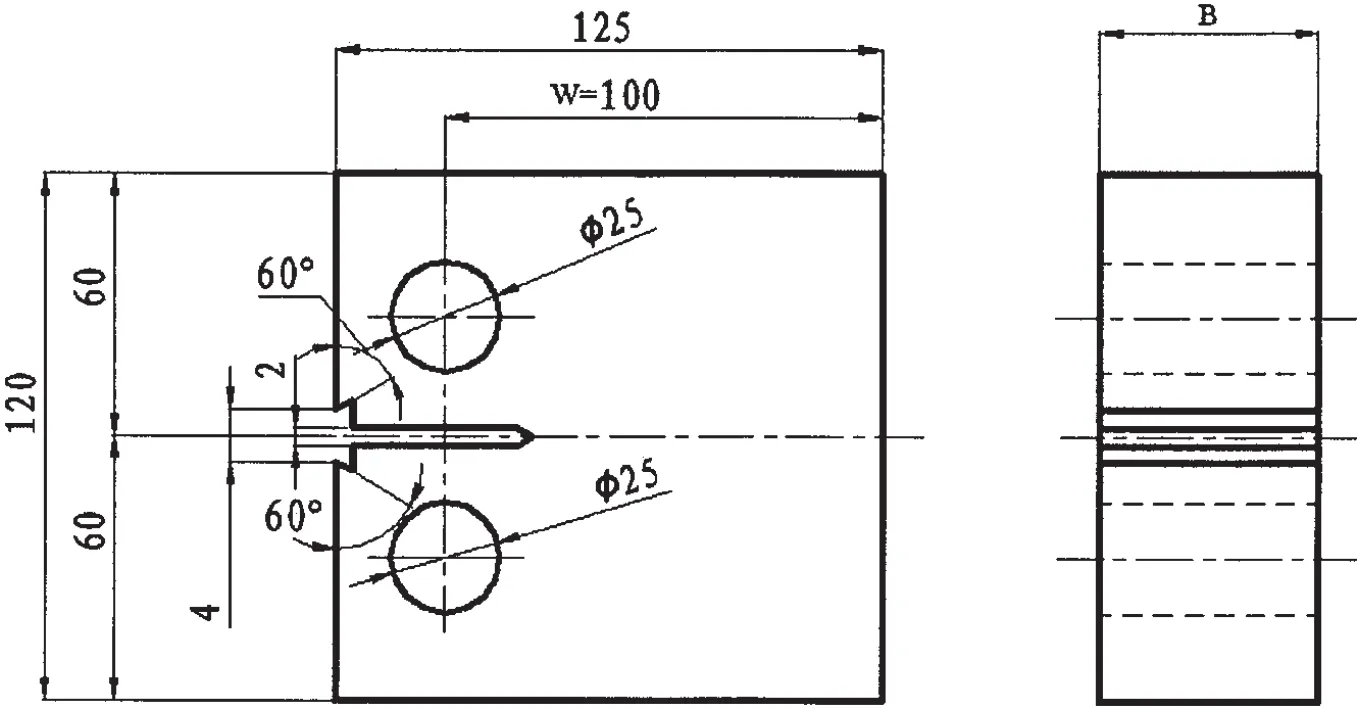
Fig.1 Dimensions of compact specimens
The fracture configuration is screened after test.Fig.2 lists five typical configurations of Ti80 when specimen thickness varies from 10 mm to 50 mm,which differs from a majority of shear yielding for thinner specimens and a majority of traction fracture for thicker specimens.Similar results can be obtained for TC4 ELI.Fig.3 and Fig.4 respectively give the tendency of KQdata of Ti80 and TC4 ELI with increasing specimen thickness.Figs.5 and 6 show the Pmax/PQratio as a function of ligament slimness.A clear rising trend is visible with increasing slimness((W-a)/B).The trend will be discussed in next section.However,most of the data exceeds the requirement P>maxQ/P≤1.1 stipulated in American standard ASTM E399[1].

Fig.2 Fracture configurations of one series of Ti80 specimens:(a)B=10 mm;(b)B=20 mm;(c)B=30 mm;(d)B=40 mm;(e)B=50 mm

Fig.3 KQdata with increasing thickness of Ti80 specimens
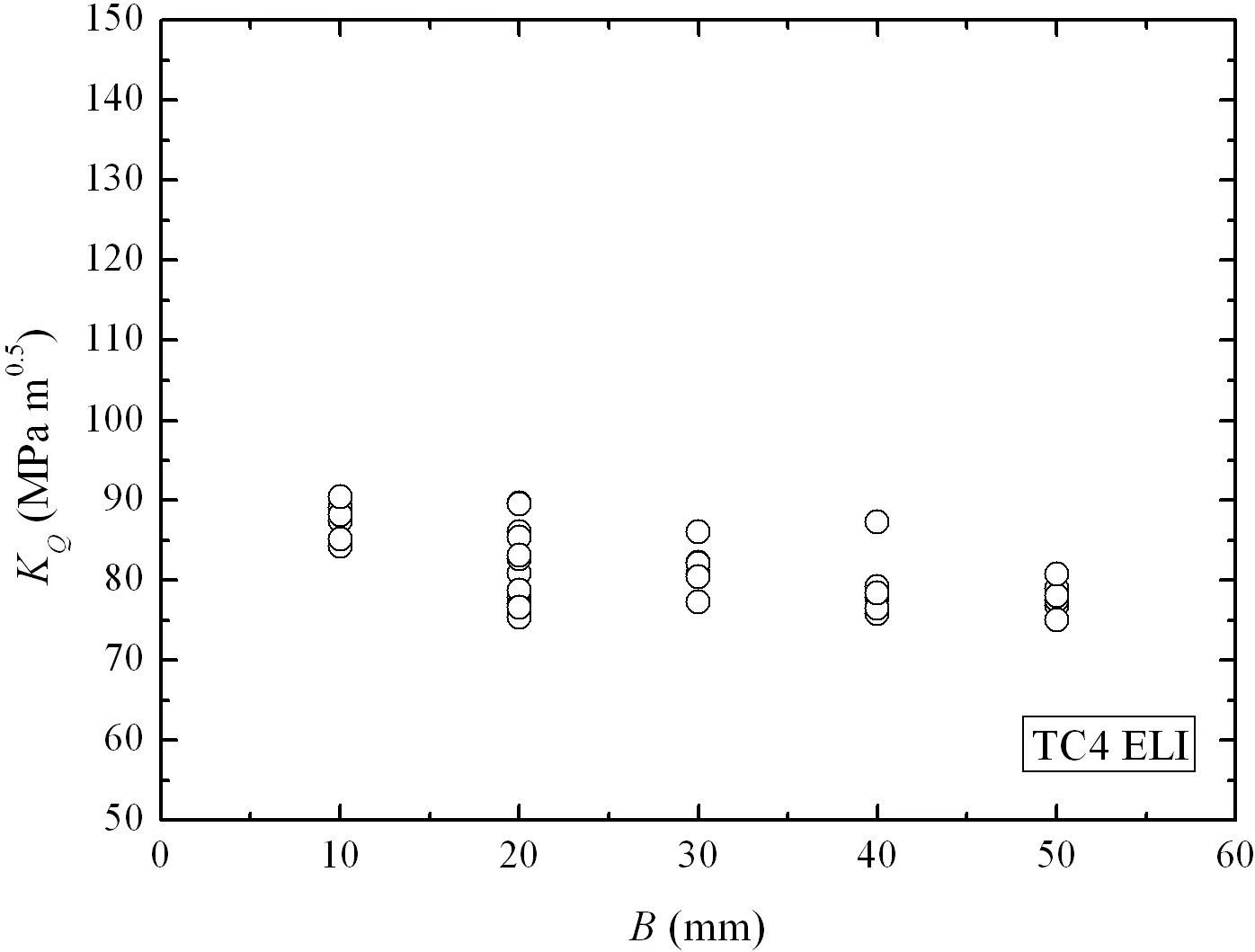
Fig.4 KQdata with increasing thickness of TC4 ELI specimens

Fig.5 Pmax/PQdata with increasing B/(W-a)of Ti80 specimens
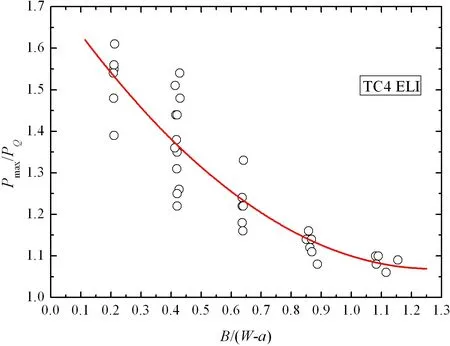
Fig.6 Pmax/PQdata with increasing B/(W-a)of TC4 ELI specimens
3 Results and discussions
3.1 The tendency of KQ
From Figs.3 and 4,it can be seen that the fracture toughness nearly keeps constant with increasing thickness.It is supposed that though the specimen thickness varies,their shearing resistance curve may be similar during testing.A simplified analysis will be used as follows to validate the testing results.
In a linear elastic situation,the crack driving force KIis a function of load and crack length,

The ductile tearing resistance of the material can usually be approximated by a power law expression,

For standard CT specimen,
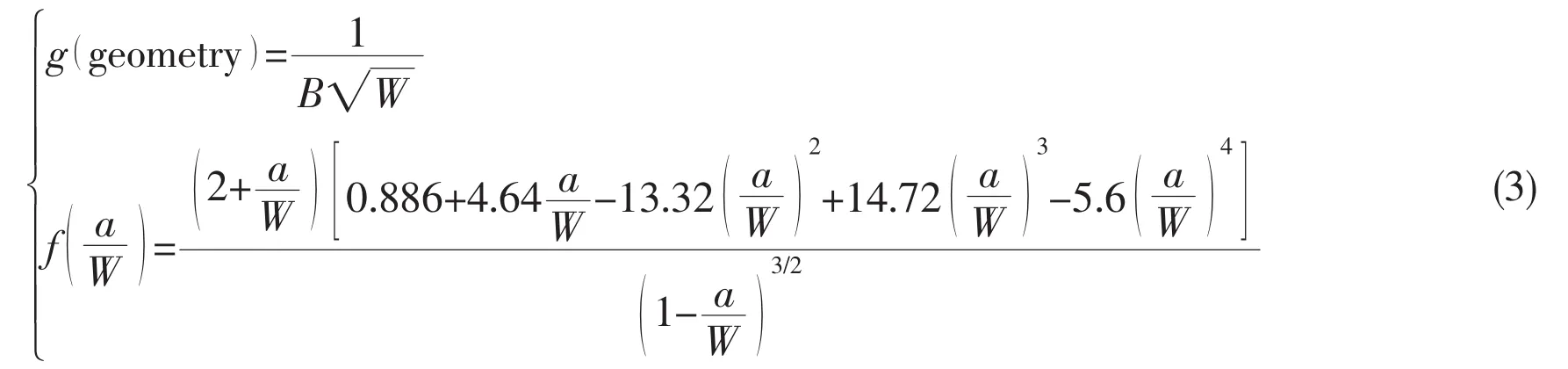
The crack size can be calculated using the crack mouth opening compliance measurements.For compact specimen,the following equations can be adopted[2],
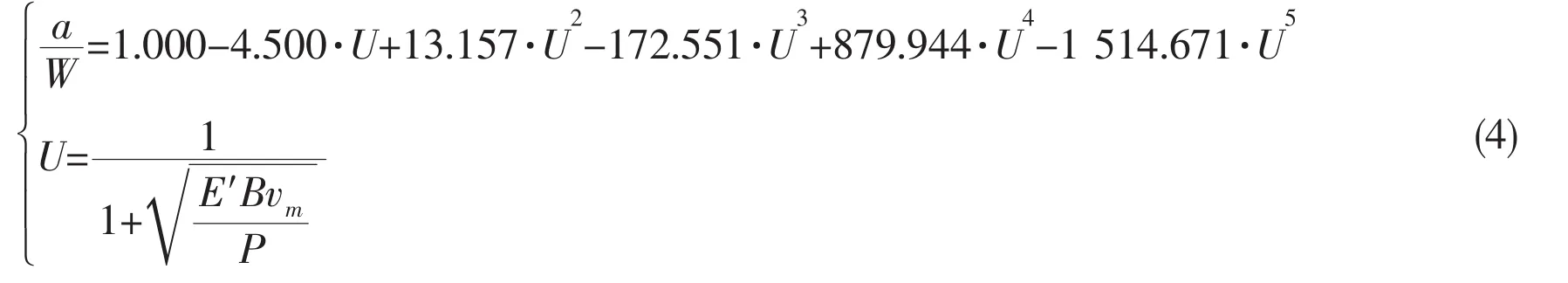
where E′is the elastic constraint modulus.
Then,the method from P-vmcurve to tearing resistance KI-Δa curve can be obtained by combining Eqs.(1)-(4).As an example,to take a series of test results of Ti80 for an illustration.The P-vmcurve is shown in Fig.7.And the transformed tearing resistance curve can be seen in Fig.8.The results indicate that the tearing resistance curve for this material is unaffected by specimen ligament geometry during the thickness region we adopted in our test.However,it can be seen that the resistance curve for 10 mm specimen has become steeper than others.It is assumed that the tendency is related to the slimness of the specimen,namely,(W-a)/B.when the ligament geometry becomes slim enough,the tearing resistance curve will start to become increasingly steeper.Further research is needed for more persuasive conclusion.

Fig.7 Load(F)vs.crack mouth opening displacement(v)for one series of Ti80 specimens
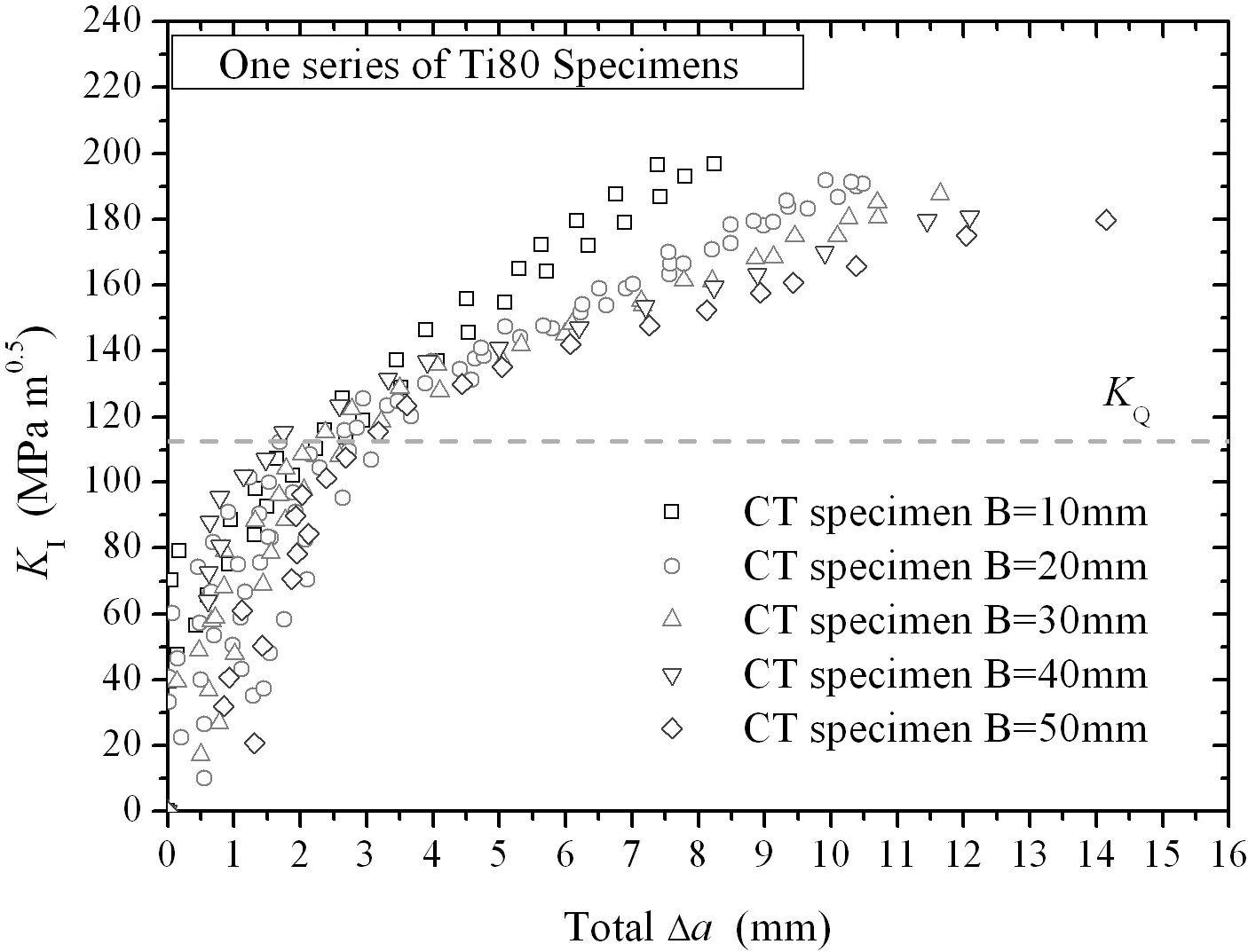
Fig.8 Tearing resistance curve for one series of Ti80 specimens
3.2 The tendency of Pmax/PQ
Ductile crack growth in a plane sided specimen occurs mainly in the center of the specimen.The crack growth at the side surface of the specimen is suppressed,causing the crack to form a tunnel shape[5],as shown in Fig.9.The phenomenon is called tunneling effect.Results show that the thickness of plate and the crack length have an evident influence on the crack tunneling.When plate thickness is smaller(B<a),crack tunneling is more evident.With the increase of thickness,the tunneling will disappear and even present opposite phenomenon when B>2a[8].
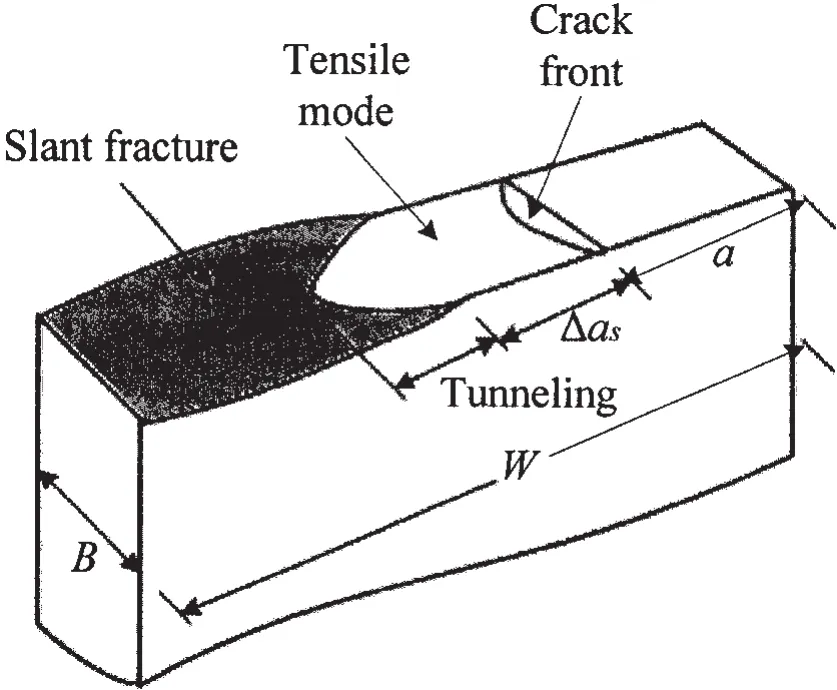
Fig.9 Fracture surface of a CT specimen
Combining Eqs.(1)and(2)enables the load to be written as a function of crack growth.Maximum load Pmaxoccurs when the derivative of the function equals zero.Thus,the amount of crack growth at maximum load for linear elastic loading can be described by,

PQcorresponds quite closely to a 2%crack growth of the ligament,in accordance with the experimental results of Munz et al(1976)[9].

Tab.1 lists the changing tendency of the ratio Pmax/PQwith a/W and m.It can be seen that the relative crack length,a/W,has a negligible effect on Pmax/PQ.The ratio is determined by steepness index,m,of tearing resistance value.
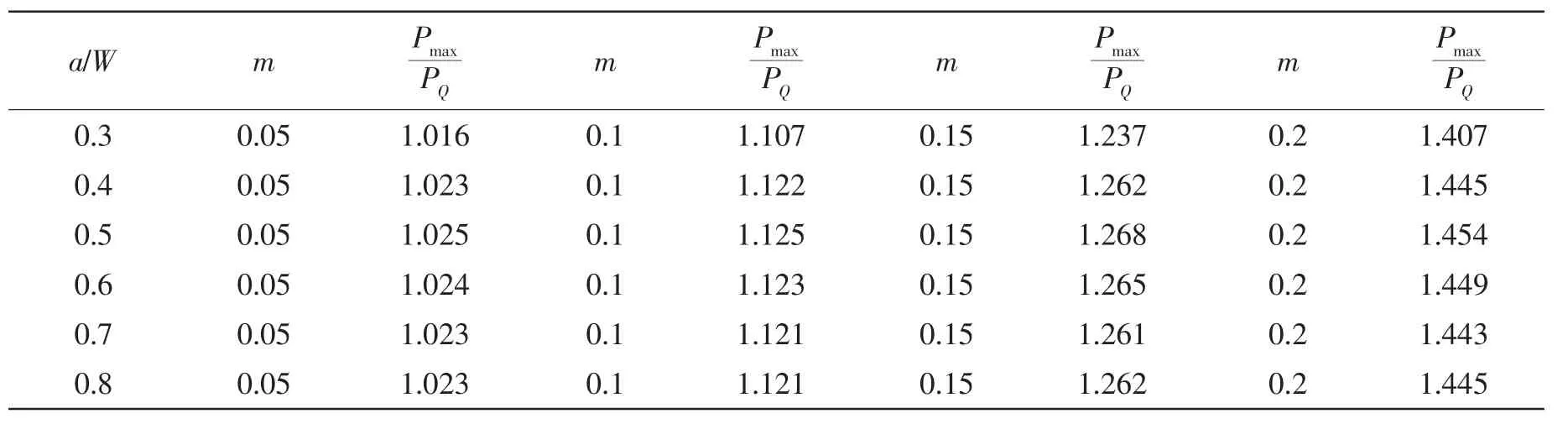
Tab.1 The dependence of Pmax/PQon steepness index,m,of tearing resistance value
Similar to the presentation by Wallin(2005)[5],for a specific ligament size W-a in our testing,the ligament slimness expressed by(W-a)/B will increase with decreasing thickness B.Ligament slimness enhances the tunneling effect,and this is the main reason for the steeper tearing resistance curve.Steeper tearing resistance means higher values of m and its corresponding Pmax/PQ.Therefore,the trend of Pmax/PQvalue is due to crack tunneling effect from this point of view.However,this is a quite simplified analysis,and more persuadable investigation of theoretical justification for the criteria Pmax/PQ≤1.1 to be used as a measure of planestrain should be carried out in the future work.
4 Summary and conclusions
This paper presented the fracture toughness test results for candidate titanium alloys in submersible structures.Series of non-standard specimens are designed for test and analysis.Thickness effect is specifically investigated using specimens with similar ligament size.Some conclusions can be drawn as follows:
(1)According to current testing standards,traditional fracture toughness test with normal specimen size may not give valid value of the tested titanium alloy used in submersible structures.Larger standard specimen must be used to satisfy the requirement in the current standard but will be quite costly.Actually,a thickness less than that required for plane strain fracture in a given material is used in an engineering application.Non-standard specimens can be designed for evaluation purpose.
(2)KQnearly unpredictably keeps constant with varied specimen thickness while most of the results could not satisfy the requirement Pmax/PQ≤1.1 in the current testing standards.
(3)A simplified method is used to transform load versus crack mouth opening displacement curve to tearing resistance curve.The results indicate that the tearing resistance curve for the candidate titanium alloys is unaffected by specimen ligament geometry during the thickness region we adopted in our test.This is the reason for the nearly constant KQvalues.However,it can be seen that the resistance curve for 10 mm specimen has become steeper than others.
(4)The ligament slimness enhances the tunneling effect which is the main reason for the steeper tearing resistance curve when the specimen is thinner.Steeper tearing resistance curve will result in higher Pmax/PQ.However,more persuadable investigation of theoretical justification for the criteria Pmax/PQ≤1.1 to be used as a measure of plane-strain should be carried out in the future study.
Acknowledgement
This work is supported by High-tech 863 Program under the project of“Development of a 4 500 m deep manned submersible”(Project No.2009AA093303)and Fourth Term of“333 Engineering”Program of Jiangsu Province under the project of“Fatigue and fracture performance of domestically produced high strength titanium alloys for the 4 500 m deep manned pressure hull”(Project No.BRA2011116).
[1]ASTM E399-90.Standard of test method for plain strain fracture toughness of metallic materials[S].America Society of Testing and Materials,1990.
[2]ASTM E399-09ε2.Standard test method for linear-elastic plain-strain fracture toughness KIC of metallic materials[S].America Society of Testing and Materials,2010.
[3]Jones M H,Brown W F Jr.The influence of crack length and thickness in plane strain fracture toughness tests,review of developments in plane strain fracture toughness testing,ASTM STP 463[R].American Society for Testing and Materials,Philadelphia,1970:63-101.
[4]Gao Y F.The discussion about KICvalid criterion in our national fracture toughness testing method[C]//CSTAM2011,Aug.22-24.Harbin,China,2011.
[5]Wallin K R W.Critical assessment of the standard ASTM E 399[J].Fatigue and Fracture Mechanics,Journal of ASTM International,2005,2(5):433-453.
[6]Guo W L,Pitt S D,Jones R.An equivalent thickness concept for fracture of general three dimensional cracks[C]//Proceedings of the International Conference on Strength Theory.Xi′an,China,Sep.1998.
[7]Li L,Song D J.Microstructure and processing map of hot compressing deformation of Ti80 alloy[J].The Chinese Journal of Nonferrous Metals,2010,20(S1):S739-S742.
[8]Wu Z X,The behaviors of crack tunneling and the effecting factors[J].Chinese Journal of Materials Research,2007,21:264-267.
[9]Munz D,Galda K H,Link F.Effect of specimen size on fracture toughness of a titanium alloy[J].Mechanics of Crack Growth,ASTM STP 590,ASTM International,West Conshohocken,PA,1976:219-234.
- 船舶力学的其它文章
- Experimental Study of the Motion Responses of a Large Mooring(LNG)Ship in the Waves with Grand Period
- CLSVOF Method for Violent Sloshing with Impact Load in Tanks under Shallow Water Depth
- A New Method for Predicting the Steady Performance of Ducted Propeller with Stators
- Experimental Research on Hydrodynamic Characteristics of Propeller in Waves
- Research on Method for Optimization Design of Riblets Angle based on CFD Techniques
- Online Prediction of Ship Rolling based on Varying Parameters LSSVM

