单基线载波相位双差定位、位置差分和单点定位的精度分析

王霞迎，秘金钟

(中国测绘科学研究院，北京100830)

一、引 言

GPS由于其高精度、全天候、实时性、无通视条件限制等优点，已经广泛应用于GPS数据处理当中。GPS原始测量数据受接收机钟差、对流层和电离层误差、多路径效应、卫星轨道等误差的影响，数据处理中需对这些误差加以改正，而GPS载波相位双差处理的方法消除了其中的大部分误差，较为实用。现对载波相位双差模型、结果分析、注意问题逐一论述。

二、载波相位双差模型

观测方程的一般形式为

式中，i为测站;j为卫星。

基线向量的单差为

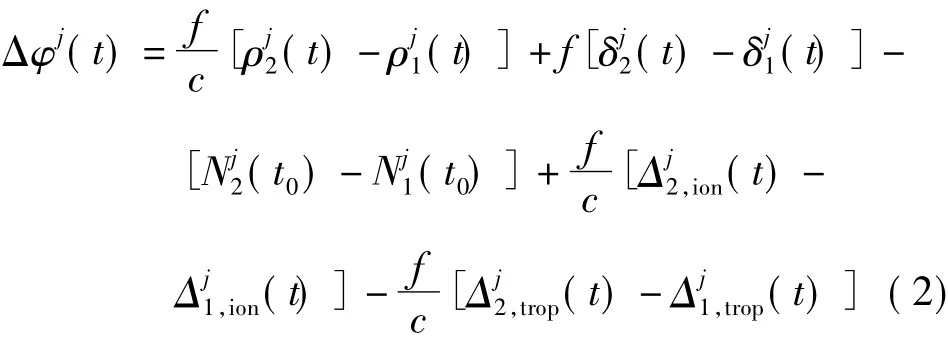
基线向量的双差(测站间求差，卫星间求差)为

以式(2)作为观测方程，组成法方程，未知数为测站坐标和整周模糊度。

三、数据处理及结果分析

基准站采用北京房山IGS站的观测数据，流动站采用位于中国测绘科学研究院的流动站，分析了30 min的观测数据，采样率为15 s，两个测站在整个观测过程跟踪了7颗共视卫星。下面分别对载波相位双差观测结果(如图1～图3所示)、位置差分[1](如图4～图6所示)、单点定位(如图7～图9所示)结果分析。

图1 载波相位双差X方向的偏差

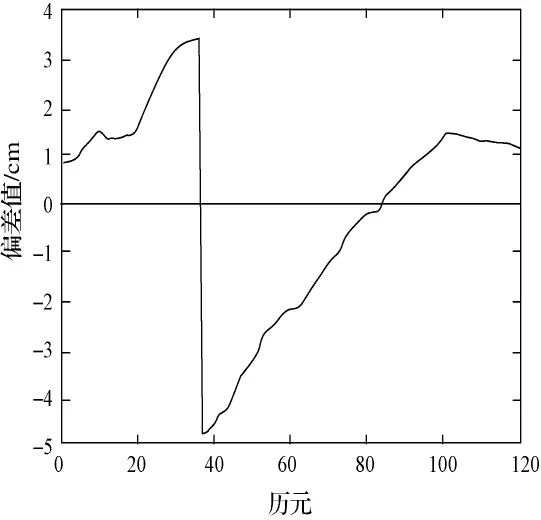
图2 载波相位双差Y方向偏差

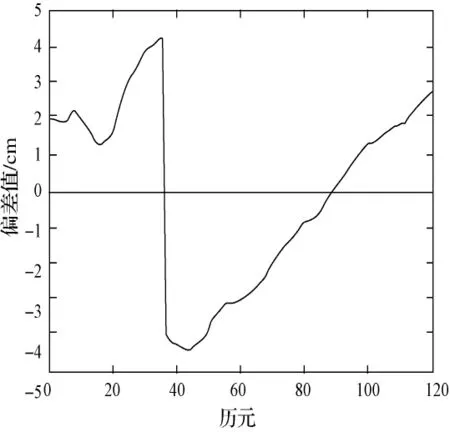
图3 载波相位双差Z方向偏差

图4 位置差分X方向偏差

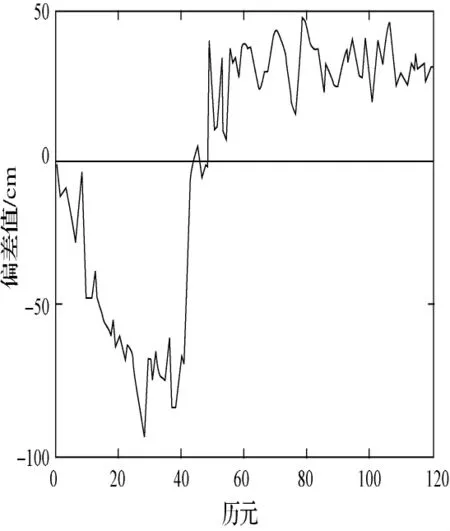
图5 位置差分Y方向偏差

图6 位置差分Z方向偏差

图7 单点定位X方向偏差

图8 单点定位Y方向偏差

图9 单点定位Z方向偏差

由图中可得，载波相位双差X方向数据误差较小，Y和Z方向在将近第40历元的时候出现大的突变，整体还是控制在5 cm以内，已经满足在大多数工程的数据解算要求。同时，与位置差分、单点定位相比，其结果精度大大提高。

四、注意问题

1．基线长度限制

对于短基线(＜20 km)，信号传输过程误差(如对流层、电离层)、接收机钟差、卫星钟差、卫星轨道误差大部分可以消除，并求解整周模糊度，可以提高测站的定位精度。但是对于较长基线，模糊无需求整，可直接用作浮点解来代入法方程求解测站位置。

2．起算点坐标

基准站起算坐标的精确与否直接关系到流动站测站坐标的解算。因此，为了保证结果的准确性，使用国家级控制点，或预先使用接收机在基准站较长时间观测求解起点坐标。

3．卫星高度角的选择

为了尽量避免多路径效应的影响及卫星几何强度较差，通常选取的卫星高度角要大于15°。

4．参考卫星的选取

在组成误差方程时，选择每个历元中卫星高度角都较大的一个最优参考星，通常要大于70°。

5．观测时段的选取

观测时段不宜过长，以15min～30min为宜，时间过短多余观测不足，时间过长则前后相关性减弱。

6．评定精度

短基线解算中评定指标有：PDOP、VDOP、HDOP、中误差。

1)PDOP：模糊度次优解与最优解之比，反应卫星的分布情况。

2)VDOP：垂直精度因子，反应测站坐标垂直方向的误差。

3)HDOP：水平精度因子，反应测站坐标水平方向的误差。

4)中误差：反应观测误差对测站坐标精度的影响。

五、结束语

本文对位置差分和双差载波相差分两种进行编程实现，并对比了3种方法解算结果精度，证明了载波相位双差的精度较高。简述了在编写程序中遇到的问题，并提出合理的建议，希望为载波相位差分程序提供一些帮助。

[1]党亚民，秘金钟，成英燕．全球导航卫星系统原理与应用[M]．北京：测绘出版社，2007年．

[2]蔡艳辉，程鹏飞，李夕银．整周模糊度去相关的两种实现方法[J]．测绘工程，2003，12(4)：36-38．

[3]刘大杰，施一民，过静君．全球定位系统(GPS)的原理与数据处理[M]．上海：同济大学出版社，1997．

[4]TEUNISSEN P．G．The Least-square Ambiguity Decorrelation Adjustment：A Method for Fast GPS Integer Ambiguity Estimation[J]．Journal of Geodesy，1995，70(1-2)：65-82．