大地坐标系中多边形面积计算方法研究

曹振宇，谭明建，沈艳敏

(1.武汉大学测绘遥感信息工程国家重点实验室，湖北武汉430079;2.四川省基础地理信息中心，四川成都610041)

一、引 言

地理国情监测是测绘工作者面临的重要任务和责任工程，是地理信息更深更广层次的应用。重要地理信息是重要的人文或自然地理实体的位置、高程、面积、长度等信息。从地理信息数据挖掘、提取重要地理信息已经成为研究与应用的热点领域［1］。其中，面状分布的地理要素在GIS中常用多边形来表示。本文系统地研究了地理坐标系中多边形要素椭球面积和表面积计算的方法。

目前商业GIS(如ArcGIS)软件提供的多边形面积统计功能一般是针对平面投影坐标系数据，不适用于大地坐标系数据多边形面积计算。现有的多边形椭球面积计算方法一般基于辛普森积分，依次按照多边形顶点顺序将多边形边、通过多边形边端点的纬线以及给定经线组成梯形的面积，然后求其代数和［2-3］。尚没有文献讨论复杂多边形如有岛多边形的椭球面积计算。多边形表面积一般基于格网DEM表面面积计算，采用多边形包含栅格单元面积进行累加得到，但大家一般只讨论了投影平面直角坐标系中表面积的具体计算方法。本文首先讨论了大地坐标系中复杂多边形椭球面积计算方法，然后讨论了大地坐标系多边形表面积计算方法。

二、相关定义

1.多边形

多边形由首尾相连的弧段构成。如图1所示，多边形包含内外边界弧段，按左手法则，其中边界弧段的正向对应多边形内部，负向对应的区域成为岛。图中P1为多边形内部，P2对应的区域即为岛。

2.椭球面积

椭球面积是指多边形在参考椭球面上的面积。

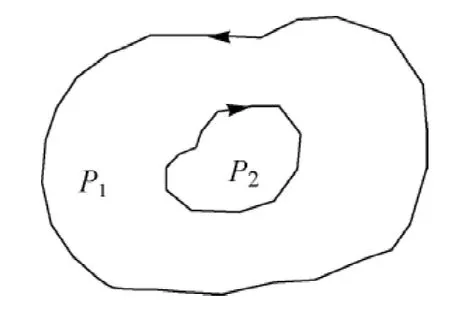
图1 多边形要素

3.表面积

本文表面积是指多边形在地形表面上的曲面面积。

三、复杂多边形椭球面积计算方法

1.基于辛普森积分多边形椭球面积计算方法

如图2所示，多边形ABCD的面积就等于4个梯形图块(ABB1A1、BCC1B1、CDD1C1、DAA1D1)面积的代数和。L0为任意经线。任意多边形面积计算按照多边形顶点顺序逐个计算相邻两点连线与任意经线构成的梯形面积Si然后累加。顶点按逆时针顺序得到的结果为正，按顺时针顺序得到的结果为负。

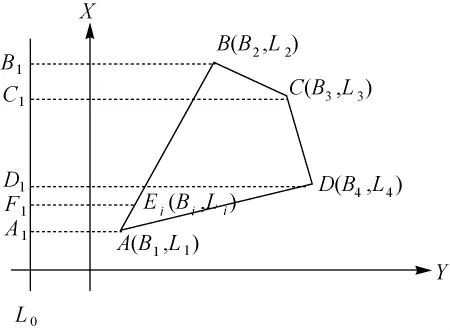
图2 椭球面上任意多边形面积计算

椭球面上任一梯形图块面积计算公式为

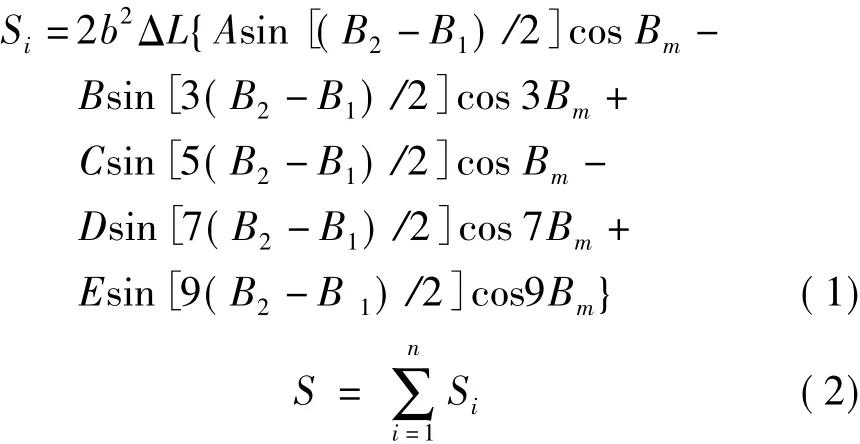
式中，A、B、C、D、E 为常数。

2.复杂多边形要素椭球面积计算方法

图3表示的复杂多边形要素包含P1和P2两个部分，由弧段 a、b、c、d、e、f组成。a、e 为外边界弧段，称为外环。b、c、d为a包含的内边界弧段，称为内环。图3中f为e包含的内环。弧段由一系列顶点构成、图3中弧段 e包含顶点(V1、V2、V3、V4、V5)。

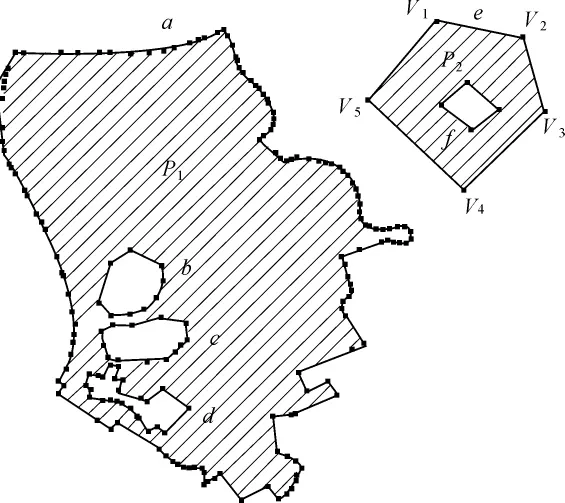
图3 复杂多边形区域

对图3所示的复杂多边形要素，采用图4所示的流程，首先遍历多边形要素的外环，按顶点顺时针顺序利用式(2)计算外环面积Si。然后遍历当前外环包含的内环，按顶点逆时针顺序利用式(2)计算内环包含的面积并求和则当前外环所在区域的面积为依次计算每个外环所在区域的面积累加即为多边形要素的椭球面积。

四、多边形表面积计算方法

多边形表面积是指多边形在地形表面上的空间曲面面积。如图5所示，规则格网表示多边形所在区域的DEM，多边形表面积S可以表示为以数字高程模型DEM、多边形Polygon为参数的函数：S=f(polygon，DEM)。

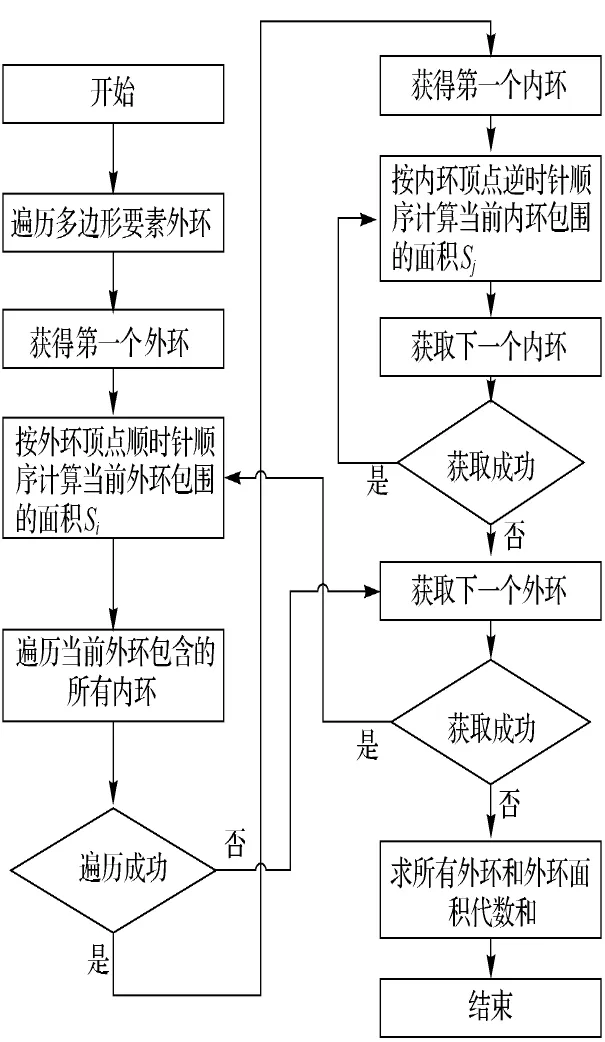
图4 复杂多边形椭球面积计算流程图

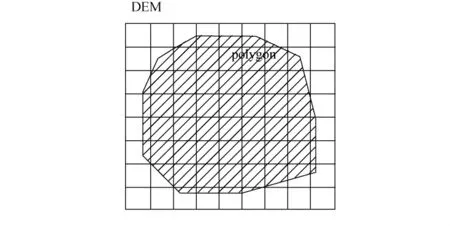
图5 基于格网DEM计算多边形表面积

多边形P的表面积计算流程如图6所示。先求P的最小外切矩形，然后将P的最小外切矩形按d x，d y大小分为n×m个格网，从DEM数据查询每个格网节点高程。然后遍历格网中所有矩形，判断矩形和P的位置关系，格网矩形和多边形的关系有分离、包含和相交3种。对包含在多边形P的矩形格网分割成两个三角形，按式(4)计算矩形格网的表面积。

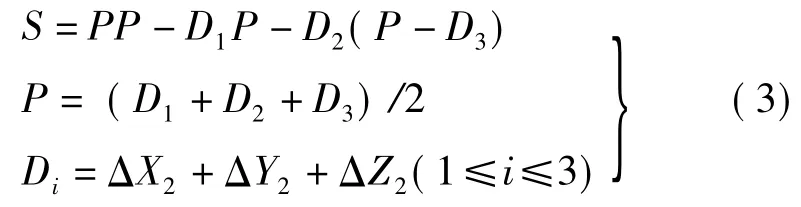
和多边形相交的矩形格网先计算矩形格网的粗糙度 CZ=S表面积/S椭球面积，然后根据文中复杂多边形椭球面积的计算方法计算相交部分的椭球面积S相交椭球面积，则相交部分的表面积为：S=CZ×S相交椭球面积。

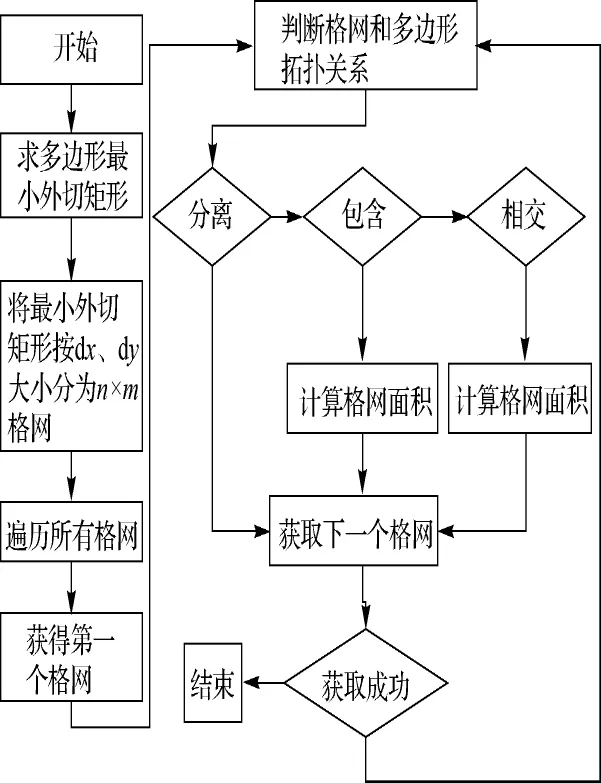
图6 多边形表面积计算流程图

多边形表面积是所有包含在多边形中格网表面积和所有与多边形相交的格网相交部分表面积的累加。

五、试验和结论

按照本文提出的椭球面积和表面积的计算方法，利用1∶50 000数字高程模型和行政境界数据，计算了县级行政区域的椭球面积和表面积。试验结果见表1。

试验结果表明，本文提出的多边形椭球面积和表面积计算方法，满足任意复杂多边形要素椭球面积和表面积计算的需要，并可以由此计算出如地形粗糙度等地形因子，因此可以用于重要地理信息统计工作。

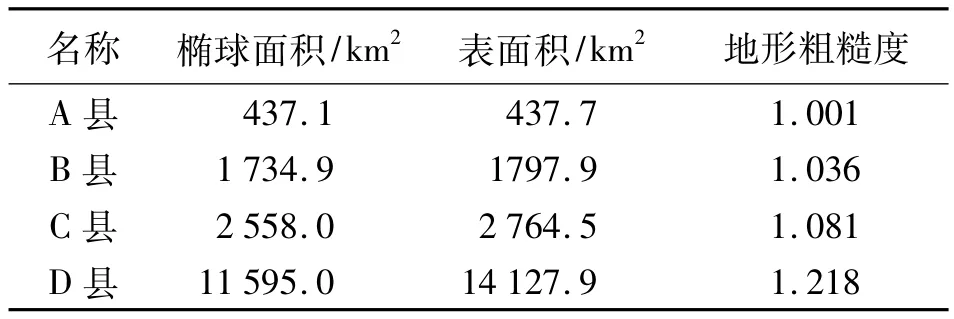
表1 县级行政区域面积计算结果

［1］蒋捷，黄蔚，王茜，等.基于数字地形图数据的重要地理信息统计分析方法初探［J］.测绘科学，2008，33(S1)：93-95.

［2］卫东.山西省重要地理信息统计分析系统设计与实现［J］.华北国土资源，2010(4)：57-60.

［3］陈娅婷，严泰来，朱德海.基于辛普森面积的多边形凹凸性识别算法［J］.地理与地理信息科学，2010，26(6)：28-30.

［4］王秀云，陈晔，周厚华，等.DEM在林地资源表面积调查中的应用［J］.南京师范大学学报：工程技术版，2006，6(1)：10-16.

［5］赵强，胡娟.MAPGIS软件中土地利用现状面积量算方法探讨［J］.国土资源导刊：湖南，2007，4(5)：58-60.

［6］李志林，朱庆.数字高程模型［M］.武汉：武汉大学出版社，2007.

［7］吴立新，史文中.地理信息系统原理与算法［M］.北京：科学出版社，2003.