基于PPP技术的测控设备精度鉴定方法研究

周 巍，郝金明，马国元，冯淑萍

(1．信息工程大学地理空间信息学院，河南 郑州450052;2．63883部队，河南 洛阳471003;3．西安测绘信息技术总站，陕西西安710054)

一、引 言

精度鉴定用于对航天测控设备的动态性能和精度进行检验和评估，分析其误差变化规律，检验其技战指标是否满足设计要求[1]，是测控设备获取准确目标测量数据的前提，具有重要意义。

目前，GPS相对定位技术已广泛应用于精度鉴定试验中，并取得了理想的效果。但为了保证解算的可靠性和精度，往往要求地面布设一定密度的GPS基准站进行同步观测，这种模式影响了作业效率，并提高了作业成本。对于一些难以到达的地区，根本无法保证足够密度的基准站，甚至找不到近距离的基准站，误差相关性大大降低，因此需要新的作业方式克服相对定位的缺点。

近年来，国内外一些著名的科研机构一直致力于精密单点定位(PPP)技术的研究[2-3]。该方法只需单台GPS接收机作业，无须与基准站联合观测，即可获得高精度绝对坐标，为测控设备精度鉴定比对标准数据的获取提供了新的解决方案。本文对PPP关键技术进行了详细分析，并在此基础上设计实现了基于PPP技术的测控设备精度鉴定系统，且利用动态实测数据对PPP技术应用于测控设备精度鉴定的可行性进行了论证。

二、PPP关键技术研究

1．误差改正

在精密单点定位中，影响其定位结果的主要误差源可以分为3类。如表1所示。

为获取高精度定位结果，必须尽可能地消除各种误差的影响。精密单点定位中误差处理主要有两种途径：①能够使用模型准确描述的误差源，采用尽可能精确的模型进行改正，如卫星姿态引起的误差，相对论效应，地球形变等;②对于目前还无法精确模型化的误差将其作为未知参数参与估计，如对流层延迟湿分量。此外，精密单点定位中的各种误差改正模型都应该与IGS数据产品所采用的模型保持一致，否则会带来精度损失[4]。

表1 主要误差源

2．数据预处理

数据预处理的任务之一是探测出GPS观测数据中的粗差和周跳，剔除粗差、标记周跳位置，参数估计时在相应的位置增加一个模糊度参数。本文采用综合TurboEdit法对粗差和周跳进行探测。

1990年美国学者Geoffrey Blewitt提出用双频载波相位和P码的线性组合进行周跳和粗差探测的方法，称为 TurboEdit方法[5]。TurboEdit方法进行周跳探测的过程可分为以下两个步骤。

1)MW(Melbourne-Wubbena)组合进行粗差和周跳探测。

MW组合观测量bδ可表示如下

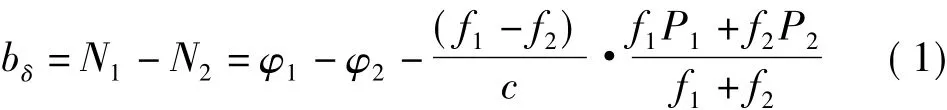
式中，φ1，φ2为两个频率的载波相位观测量。MW组合消除了几何距离部分，同时不受电离层、对流层、卫星钟差、接收机钟差和其他系统误差影响，只剩下模糊度项。在没有周跳的情况下，bδ表现为一变化约为1～2周的近似常量。采用递推的方法求bδ的平均值＜bδ＞i和均方根误差σi

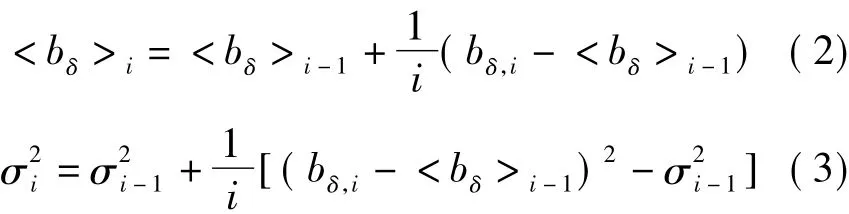
式中，bδ，i为第i历元的MW组合观测量。利用下面的公式可以进行粗差和周跳的判断。

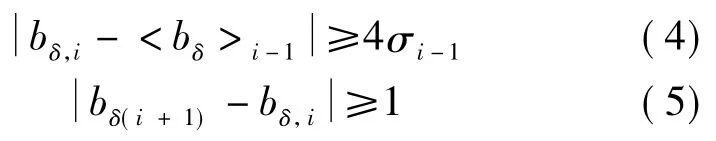
若式(4)成立且式(5)不成立，则认为i-1和i历元之间有周跳;若两式都成立，则认为第i历元存在粗差。很显然，当两个载波观测量发生相同大小的周跳时，上述方法无法探测出周跳。

2)电离层组合(Ionospheric Combination)探测周跳。

电离层组合可定义如下

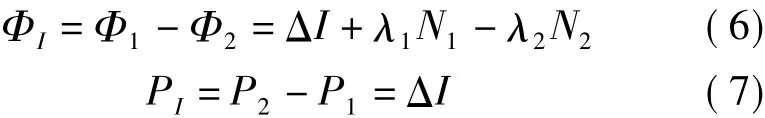
式中，ΔI为两个频率的电离层延迟之差;ΦI，PI为电离层组合相位和码。码的观测噪声较大，因此不能直接用ΦI，PI进行周跳探测。对于MW组合探测没有周跳的数据段，先对PI(i)进行多项式拟合生成Qi，多项式阶数M=min( N/100+1，6)。其中，N为该数据段的历元个数。通过以下关系式来判断粗差和周跳。

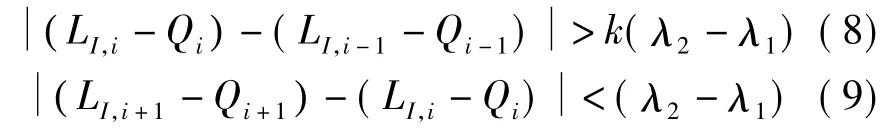
若(8)式和(9)式同时成立，则认为第i历元有周跳;若仅(8)式成立就认为第i历元存在粗差。其中k为阈值系数，Blewitt建议根据观测地区的电离层状况来确定，通常可以取k=6。

3．参数估计

本文使用递归最小二乘进行参数估计。其核心思想是分类处理不同的参数。递归最小二乘有别于传统的最小二乘方法，它通过灵活的参数分类和消去技术，保证了运算的高效，同时又不需要考虑系统的状态方程[7-8]。

将精密单点定位中所有的待估参数分为两类，设为X和Y向量。其中，X向量包含测站坐标、接收机钟差参数;Y向量包括模糊度参数及天顶对流层延迟;P为权矩阵。观测方程可重新描述如下

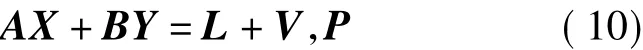
采用消参数法将X从观测方程(10)中消去，得到式(10)的法方程

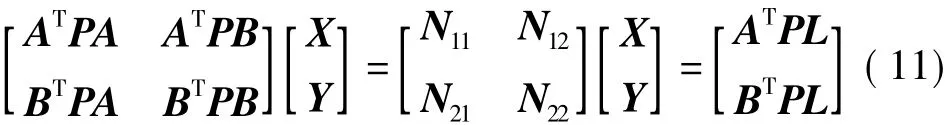
定义Z=N21N-111，将式(11)进行变换得到

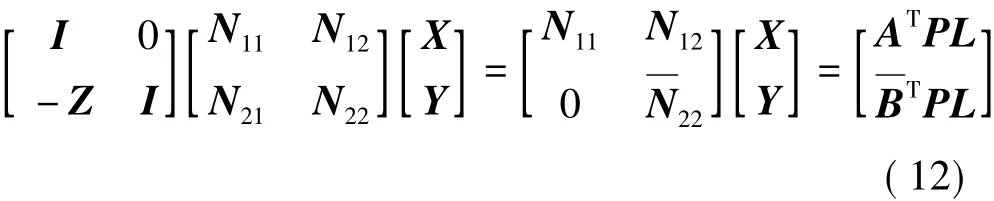
式中

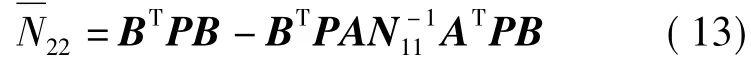
令

式(13)可表示为

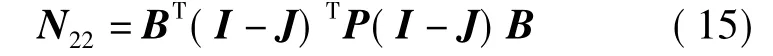
令

得到新的法方程

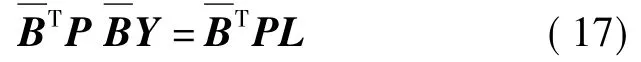
上述新的法方程等价于构成一个新的观测方程

式(18)中只剩下Y向量，即只包含了模糊度参数和对流层延迟改正参数，消除了包含测站坐标和卫星钟差的X向量。同时L观测量及其权阵保持不变。因此，可以首先估计出Y向量后，再由下式估计X向量

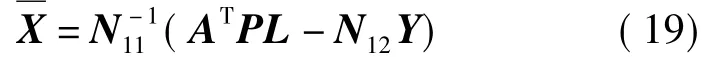
因此，通过对上述参数分类递归处理，可以大大提高数据处理的速度。

4．PPP数据处理流程

PPP算法流程如图1所示。

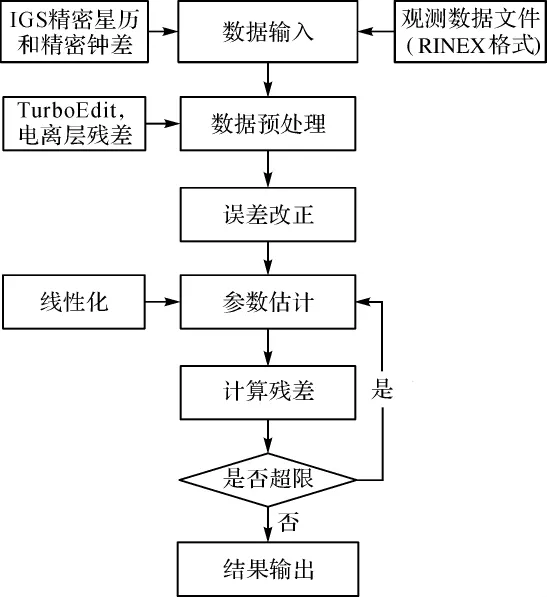
图1 PPP算法流程图

三、基于PPP技术的测控设备精度鉴定系统组成及应用模式

精度鉴定系统为被鉴定设备提供比对标准数据，并为机组人员及地面测量设备提供导航信息，主要分为机载测量分系统、机载导航分系统、数据处理分系统、地面航路显示分系统。其组成如图2所示。

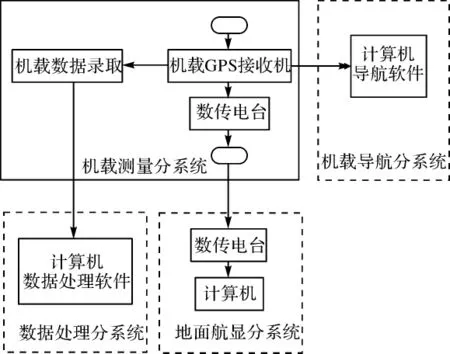
图2 精度鉴定系统组成

图3为精度鉴定系统应用模式。其中，飞机平台搭载GPS测量设备和合作目标，机载测量分系统完成观测数据采集并为机载导航分系统和地面航路显示分系统提供导航信息。数据处理分系统由PPP数据处理软件、精度鉴定综合数据处理软件、计算机等构成。PPP数据处理软件利用机载测量分系统采集的观测数据解算出合作目标在飞行航路上的位置信息，并作为比对标准数据提交给综合数据处理软件，完成对测控设备动态精度的分析。

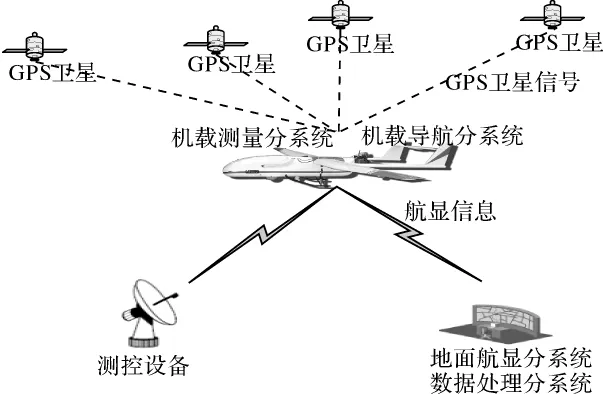
图3 精度鉴定系统应用模式

四、试验结果分析

采用机载和船载实测数据进行试验分析，将NovAtel公司GrafNav 7．8软件载波相位动态相对定位的结果作为“真值”，并将精密单点定位结果与“真值”比较，通过统计ENU 3个方向的均方根误差RMS和最大误差MAX来评价PPP定位结果的外符合精度。

1．机载GPS数据PPP动态定位精度分析

收集了一个航空测量试验的GPS实测数据，数据采样间隔为1 s，历时2 h。图4和图5的分别显示了飞机的平面飞行轨迹和高程变化曲线。飞机的机动情况体现了航空测量的实际，具有典型性。

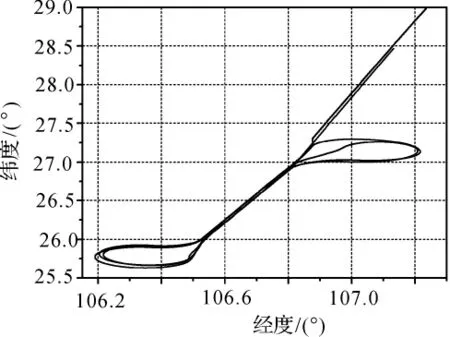
图4 飞机平面运行轨迹

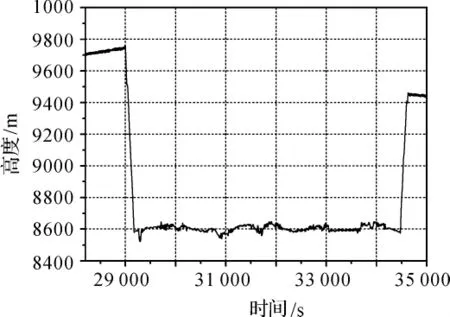
图5 飞机运行高程变化

图6显示了机载动态精密单点定位解算结果与“真值”比较在ENU 3个方向的差值，结果统计如表2所示。

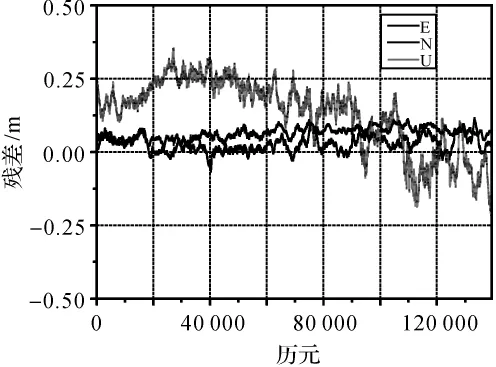
图6 动态PPP解算结果与双差解坐标在NEU方向上的差值

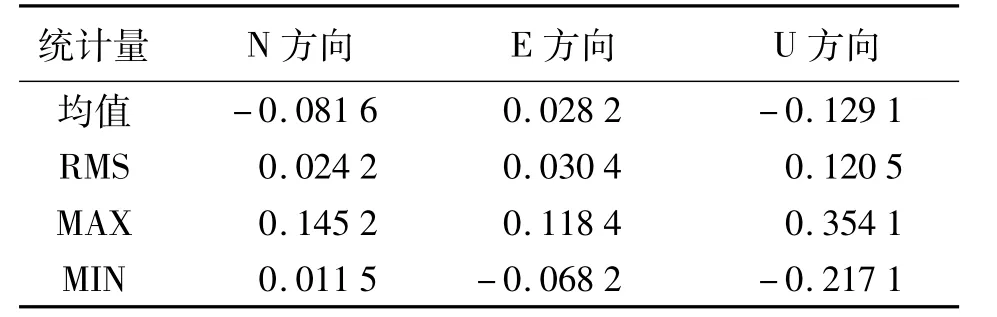
表2 定位误差统计 m

NEU方向的 RMS 值依次为：0．024 m、0．030 m、0．096m;平面方向精度为4 cm，高程方向精度为12 cm。

2．船载GPS数据PPP动态定位精度分析

海上测量GPS数据来自于我国东部某近海海域的海上测量实验。数据采样间隔为1 s，历时2 h，在岸边架设有基准站，实验船的航行路线见图7～图8所示。

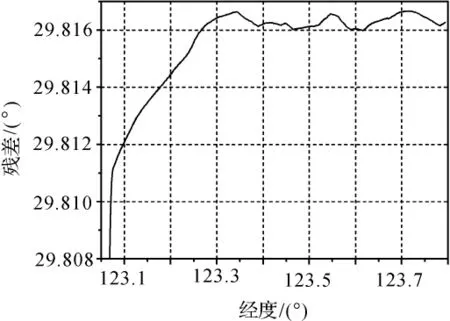
图7 平面运行轨迹

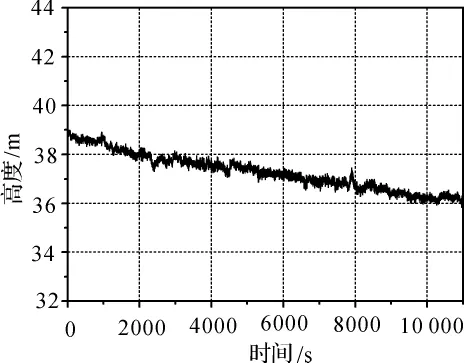
图8 高程变化

PPP动态解算结果与“真值”比较在ENU 3个方向的差值如图9和表3所示。NEU方向的RMS值依次为：0．033 m、0．072m、0．120 m;平面方向经度为8 cm，高程方向精度为12 cm。

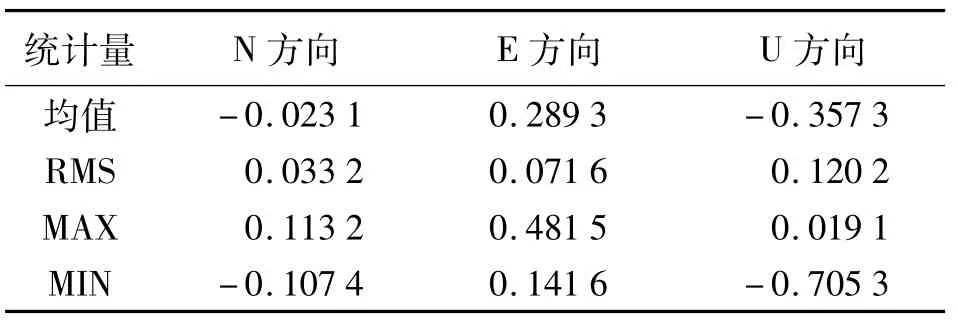
表3 定位误差统计 m

图9 船载动态PPP解算精度

通过以上机载和船载实测数据试验分析结果表明：精密单点定位解算结果与差分定位结果符合程度良好，其定位精度远高于被鉴定设备，可应用于测控设备精度鉴定试验，为其提供标准比对数据。

五、结束语

本文探讨了GPS非差精密单点定位关键技术，设计开发了基于GPS精密单点定位技术的测控设备精度鉴定系统，对大量实例数据进行了试验与分析，结果表明：GPS精密单点定位精度能满足工程需求，其简单、高效、低成本的作业方式为测控设备精度鉴定提供了新的解决方案。

[1]解海中，张守信，董旭荣，等．航天测控设备GPS精度鉴定方法研究[J]．指挥技术学院学报，1999，10(3)：30-36．

[2]ZHANG X．Precise Point Positioning Evaluation and Airborne Lidar Calibration[R]．Danish National Space Center，2005．

[3]袁修孝，付建红，楼益栋．基于精密单点定位技术的GPS辅助空中三角测量[J]．测绘学报，2007，36(3)：252-255．

[4]KOUBA J．A Guide to Using International GPS Service(IGS)Products[EB/OL]．ftp：∥igscb．jpl．nasa．gov/igscb/resource/pubs/GuidetoUsingIGSProducts．pdf．

[5]BLEWITTG．An Automatic Editing Algorithm for GPSData[J]．Geophysical Research Letter，1990，17(3)：199-202．

[6]刘基余．GPS卫星导航原理与定位方法[M]．2版．北京：测绘出版社，2008．

[7]魏子卿，葛茂荣．GPS相对定位的数学模型[M]．北京：测绘出版社，1997：182．

[8]GOAD C C，CHADWELL C D．Investigation for Improving GPS Orbits Using a Discrete Sequential Estimator and Stochastic Models Of Selected Physical Processes[R]．Greenbelt，Maryland：Goddard Space Flight Center，1993：42．