上海天文台φ65m射电望远镜精密安装测量

李宗春，李广云，冯其强，李 干，李国俊，曹 林

(1．信息工程大学地理空间信息学院，河南郑州450052;2．72946部队，山东 淄博255020)

一、工程概况

上海天文台 φ65 m射电望远镜(以下简称“65m天线”，见图1，其技术指标见表1)是一台国内领先、亚洲最大、国际先进的全天线可转动的大型射电望远镜，在同类型的望远镜中总体性能上位列全球第四。该望远镜将在射电天文、天文地球动力学和空间科学等多种学科中成为我国乃至世界上一台主干观测设备，做出一流的科学成果。65 m天线作为一个单元参加中国VLBI网，灵敏度将提高42%;参加欧洲VLBI网，将使其灵敏度提高15～35%;在东亚VLBI网中起到主导作用。在航天工程的应用中，可以为探月二、三期工程、火星探测及其他深空探测工程做出更大贡献。

图1 上海天文台φ65m天线

表1 上海天文台φ65m天线技术指标

续表1

该天线结构从上到下可分为反射体、俯仰机构、方位机构3大部件。天线安装测量内容众多，本文主要关注4点：安装测量控制网的建立、天线背架快速检测、副面调整机构标定和主面摄影测量精度仿真分析。

二、安装测量控制网

65m天线位于上海市松江区佘山镇官塘北侧、七间村西侧，上海地区属于软土地质结构，不适宜布设测量墩或者布设测量墩的成本很高;而且该项目的建设周期短，测量工作介入时间较晚。上述不利条件使安装测量控制网的稳定性无法保障，需要另辟蹊径。

天线方位机构轨道内外侧的720个螺栓头具有分布均匀、结构稳定、施工过程中受干扰小等特点，适合作为控制网点，见图2。

图2 方位机构螺栓头分布图

为了保证控制网点的测量精度，设计加工了配合全站仪角隅棱镜测量的高精度测量工装，如图3所示。控制网的稳定性统计见表2。

从表2可以看出，在与控制网建立时的环境相同的条件下，6个转换参数的标准偏差都较小，恢复设计坐标系的精度相当，都约为±0．50mm，说明控制网的稳定性较好。

图3 配合螺栓头测量工装

表2 恢复坐标系20次结果统计

三、天线背架快速检测

如图4所示，65 m天线背架呈圆对称性分布，共分为15圈。其中，1～2圈每圈有24个蘑菇头;3～6圈每圈有48个蘑菇头;7～15圈每圈有96个蘑菇头，每个蘑菇头上有一测量定位点，共计1104个。背架的安装由TDA5005全站仪工业测量系统完成，耗时140 d左右，图5为天线背架水平状态下的全貌图。

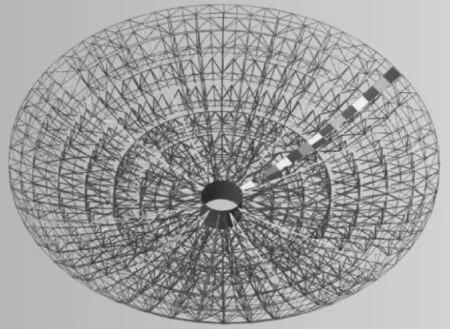
图4 65m天线背架结构示意图

天线背架几何尺寸检测的传统方法是采用全站仪或经纬仪交会测量系统进行检测[1]，其不足主要有：①测量耗时较长，效率不高;② 测量人员劳动强度大;③由于测量周期长，外在环境导致背架结构发生变形，所获背架几何尺寸数据不具有现势统一性。而激光扫描测量系统具有实时、快速、高效的特点[2]，本文引入 Riegl VZ400激光扫描仪用于65m天线背架几何尺寸快速检测。

图5 65m天线背架水平状态下全貌

根据许文学[3]的试验数据，TDA5005全站仪配合反射片在30 m范围内点位测量精度优于±0．5mm，用TDA5005全站仪的点位测量数据作为参考值，利用公共点转换法，分别将不同距离上的VZ400的测量数据与参考值进行比较，结果见表3。

由表3可以看出，VZ400扫描仪和TDA5005全站仪测量数据进行公共点转换时，如不固定尺度因子k，均方根值RMS都约为±1．0 mm;如固定尺度因子k为1，均方根值在近距离为±2．913mm，远距离为±3．966 mm，说明存在明显的尺度因子，因此可以推定VZ400扫描仪测量反射片可能存在类似于全站仪的测距加、乘常数。

表3 TDA5005和VZ400测量点位转换结果

为此，基于公共点转换模型[4]，引入激光扫描仪测距加常数C，乘常数R两个未知参数，构建8参数最小二乘平差模型解算加、乘常数。

将不同距离上的点位数据统一代入8参数模型，按最小二乘平差解算得到VZ400加、乘常数及其精度见表4。

表4 8参数模型下解算VZ400加、乘常数结果

从表4可知，常数解算有效。

将扫描仪点位数据经加、乘常数改正后与全站仪点位数据进行公共点转换得均方根值为±1．11mm。考虑到以全站仪结果作为参考数据本身有误差，扣除全站仪的影响，则在30m范围内，Riegl VZ400扫描仪系统点位测量精度约为±0．98mm。

用TDA5005全站仪检测65 m天线背架，耗时6．0 h，用 VZ400扫描仪检测65 m天线背架，耗时1．5 h，背架检测效率提高非常明显。图6为两种仪器用于背架检测的工作场景。

图6 背架检测场景

四、副面调整机构标定

65m天线副面调整机构采用Stewart机构，是一种复杂的空间多环路闭链机构，通过动平台实现对控制系统位姿的精确有效控制。但由于实际结构参数与设计结构参数存在偏差，使得机构的运动精度受到一定影响。

文献[5]提出了Stewart机构基于D-H矩阵的位姿误差计算模型;文献[6]提出基于蚁群算法的误差补偿方法。这些标定算法为遗传算法，对标定参数初值给定要求较高，且随着解算精度的提高，计算时间急剧增大。因此，本文提出了基于最小二乘法的Stewart机构标定解法。

1．误差参数的确定

图7所示为一典型的Stewart机构，机构主要由定平台、动平台、12个铰链及6个分支杆组成。根据实际要求及测量条件，本文主要研究机构本身所造成的误差。机构本身的误差参数有：

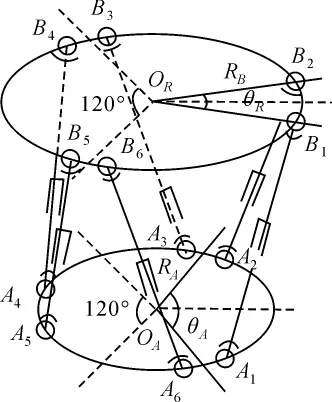
图7 Stewart机构简图

2．模型函数

标定时，在动、定平台上安置靶座，利用激光跟踪仪所测靶座坐标恢复出销孔坐标并建立动、定平台坐标系，然后以靶座坐标为公共点可解算出动、定平台相对位姿关系。根据机构运动学原理，构建包含42参数目标泛函

动平台每变换一个位姿，针对每个UPS分支可由式(1)构造出一个约束方程，因此总共可以构造6个约束方程。模型中共有42个待标定的参数，故最少需要采集7个位姿的数据。

对第i(i=1，…，6)个分支，可列误差方程矩阵形式为

式中：

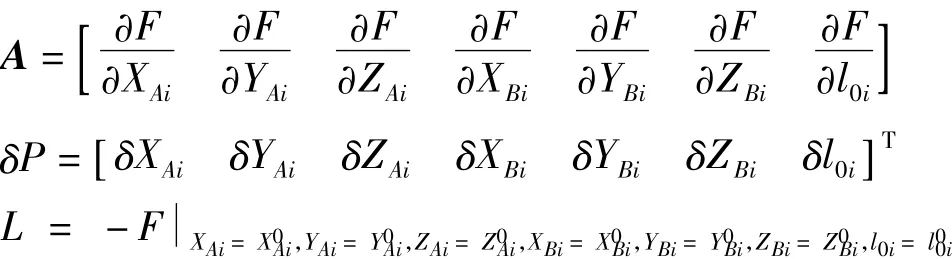
按最小二乘原理，构建法方程ATA·P=ATL，可解得δP=(ATA)-1·ATL，对于给定的各参数初值，逐次迭代直到各参数改正量δP的大小符合精度要求。表5给出了某相邻两次解算的定位精度。

表5 定位精度

从表5可知，后一次标定的运动控制精度明显高于前一次。

五、主面摄影测量精度仿真分析

鉴于天线尺寸巨大、测量精度要求高等因素，拟采用数字工业摄影测量系统进行主反射面面型精度测量[7]。一方面，由于摄站数量大、空间分布复杂，难以通过理论分析判定摄影测量精度;另一方面，测量目标尺寸较大，通过实际拍摄验证精度的代价高、风险大[8]。因此，需要利用仿真数据对摄影测量精度进行定量分析，以验证测量精度能否满足工程需求，为制定测量实施方案提供参考和依据。

1．基本思路

首先在设计坐标系下给出一定数量的物方点坐标，按某种规则确定摄站参数，计算出物方点在相应像片上的像点坐标，然后根据经验加入随机误差生成虚拟像点坐标，再由虚拟像点坐标计算出物方点坐标，与其设计值比对，以验证点位误差能否满足工程需求，寻求最优布设方案。

2．技术路线

(1)摄站规划

1)依据摄影距离、摄站环数和摄站间距，计算每一摄站位置坐标(摄站参数XS、YS、ZS)。

2)依据每一摄站位置计算其到天线的投影点及投影方向，按照像片y轴位于该位置处天线径向竖直面、像片z轴垂直于天线面的原则，计算该摄站位置处的初始摄站旋转角。

3)依据摄站前后左右4个方向的倾斜角分别计算 4 个摄站的旋转角(Rx、Ry、Rz)。

(2)虚拟像点坐标计算

1)依据物方点坐标、摄站参数及虚拟相机画幅的覆盖范围，按照共线条件方程计算物方点在相应像片的像点坐标。

2)根据经验给每一像点坐标加入一定范围的随机误差，生成虚拟像点坐标。

3)测量精度分析

依据摄影距离、摄站环数、摄站间隔、所加像点误差4个参数获得多组仿真数据。利用物方点坐标、摄站参数及像点坐标进行自检校光束法平差，将物方点坐标计算值与设计值进行公共点转换，评定不同摄站布设方案下的物方点坐标精度。

3．可行方案

通过分析仿真数据得出以下经验：摄影距离、摄站环数、摄站间隔、所加像点误差共同影响最后的平差结果;摄影距离越大、摄站间隔越大、摄站环数越小、所加像点误差越大，点位误差越大;其中摄影距离对点位误差的影响最大。

根据预先的规划，摄站布设方案要满足点位误差优于±0．1 mm，而根据摄影测量经验，现有的测量手段最高可以使像点均方根误差保证到±0．3μm。综合上述两个条件，再结合仿真中的各种限定条件，最终从所得的701组数据中选出了23组可行方案，列于表6。

表6 可行方案数据表

从表6中可以看出，摄影距离在5～6m之间的方案占了70%，而且摄站间隔很少超过8m，摄站环数接近10环。

六、结 论

1)选择天线轨道螺栓头作为安装测量控制网的控制点，保证了控制网的稳定、可靠。

2)实验发现Riegl VZ400激光扫描仪测量反射片时存在测距加、乘常数，建立了8参数最小二乘坐标转换模型，解算出的加常数、乘常数结果可信;经加、乘常数修正后，在30m范围内，VZ400点位测量外符合精度可达±1．0mm;激光扫描仪检测方法相比全站仪方法，测量效率提高了3倍。

3)试验表明，基于最小二乘法Stewart机构标定解法具有解算精度高、速度快，可满足一般工程中Stewart机构定位精度要求。

4)本文提出了通过仿真数据验证摄影测量精度的整体思路，方案可行;对实际工作的建议：在像点均方根误差接近±0．3μm的情况下，要保证点位误差优于±0．1 mm，建议将摄影距离设定在5～6m，摄站间隔不大于8m，摄站环数为10环。

[1]李宗春，李广云，汤廷松，等．某大型钢结构的精密几何检测[J]．钢结构，2003，18(3)：9-11．

[2]徐进军，张民伟．地面3维激光扫描仪：现状与发展[J]．测绘通报，2007，(1)：47-50．

[3]许文学．大型天线测量方法研究与应用[D]．郑州：信息工程大学，2007．

[4]李宗春，李广云．天线几何量测量理论及其应用[M]．测绘出版社，2009．

[5]单鹏，谢里阳，田万禄，等．基于D-H矩阵的Stewart型并联机床位姿误差计算模型[J]．机械工程学报，2010，46(17)：186-191．

[6]谢平，刘志杰，杜义浩．基于蚁群算法的并联机器人误差补偿方法[J]．计算机工程，2011，37(16)：11-13．

[7]冯其强．数字工业摄影测量系统技术研究与实践[D]．郑州：信息工程大学，2010．

[8]王保丰，李广云，李宗春，等．应用摄影测量技术检测大型天线工作状态的研究[J]．中国电子科学研究院学报，2006，1(5)：435-439．