基于CUDA的海量点云数据kNN查询算法

杨 铭，陈建峰

(上海市测绘院浦东分院，上海200129)

一、引 言

传统的kNN查询算法一般都是首先通过空间层次结构找到待查询点所处节点及其周围节点，然后对这些节点内的采样点进行距离计算，以此减少参与查询的采样点个数，从而提高查询效率。此类算法通常都是串行算法，比较适合传统的单核CPU系统，其查询效率能在一定程度上满足应用需要。然而随着三维激光扫描技术的不断发展，所能获得的点云数据量越来越大，原有的基于单核CPU的kNN查询算法的实现效率已经远远无法满足海量点云数据后处理的要求。近年来，GPU硬件性能得到了飞速提升，而nVIDIA公司推出的CUDA技术更使得我们可以利用GPU高性能的并行计算能力解决许多原来无法解决的问题。据此，本文提出了一种基于CUDA的海量点云数据快速kNN查询算法。

二、CUDA编程技术

CUDA是nVIDIA公司于2007年6月推出的一种将GPU作为数据并行计算设备的软硬件体系，其是第一种不需要借助图形学API就可以使用类C语言进行通用计算的开放环境与软件系统。由于其在性能、成本和开发时间上较传统的CPU解决方案有明显优势，CUDA的推出在学术界和产业界引起了强烈反响。现在，CUDA已经在天文学、信号处理、图像处理、模式识别、视频压缩等领域获得广泛应用，并取得了丰硕成果。

CUDA的开发十分简单，其采用了比较容易掌握的类C语言进行开发，而不需要借助任何图形学API。熟悉C语言的开发人员能够比较平稳的从CPU过渡到GPU，而不必重新学习语法。CUDA编程技术主要包含3个方面的内容：CUDA编程模型、CUDA存储器模型及CUDA软件体系。其中，CUDA编程模型将CPU作为主机，将GPU作为设备或协处理器(如图1(a)所示)，在该模型中，CPU与GPU各司其职，协同工作，它们各自拥有相互独立的存储器地址空间：主机端的内存和设备端的显存。除了编程模型，CUDA也规定了存储器模型。在程序运行期间，CUDA线程可以访问处于多个不同存储器空间中的数据(如图1(b)所示)。CUDA的软件体系则由3个层次构成：CUDA driver API、CUDA runtime API和 CUDA Library(如图 1(c)所示)。CUDA软件体系的核心是CUDA C语言，其包含C语言的最小扩展集和一个运行时库，使用这些扩展与运行时库的源文件必须通过nvcc编译器进行编译。

三、基于CUDA的穷举式kNN查询

kNN查询算法虽然经过多年研究已基本发展成熟，但在某些情况下其效率仍然不尽如人意。近年来，随着GPU硬件的快速发展，基于GPU的通用计算技术已被广泛应用于众多计算密集型领域。本章将根据 GPU软硬件的特性，提出一种通过CUDA实现的穷举式kNN查询算法。

1．算法基本流程

假设R为一个包含有m个点的d维参考点集，而Q是一个在同一空间中包含有n个点的查询点集。kNN查询的任务就是根据某一距离计算原则，在点集R中找到每个查询点的k个最近邻域点。对于穷举式kNN算法(以下简称BF-kNN)，其基本流程如图2所示。

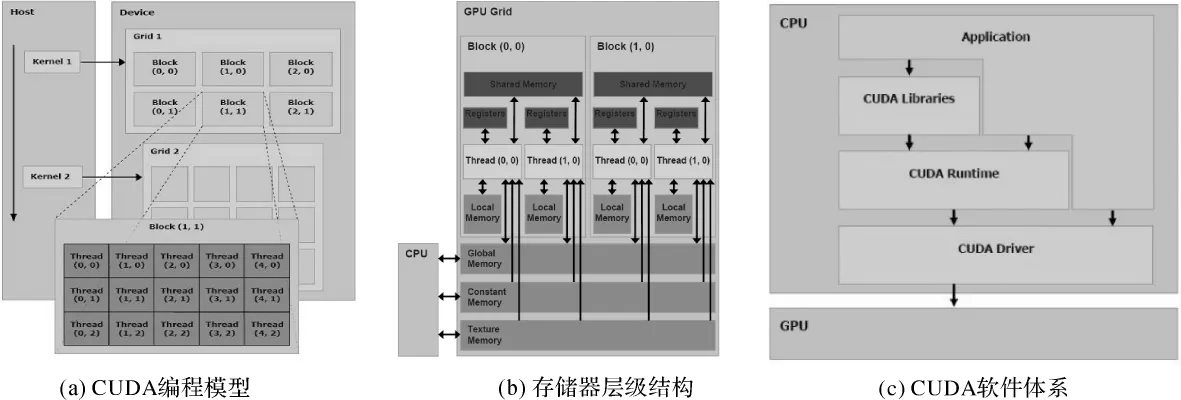
图1 CUDA编程技术

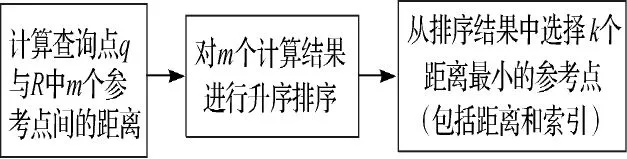
图2 穷举式kNN算法的基本流程

不难发现，上述算法的时间复杂度非常巨大：进行n×m次距离计算的时间复杂度为O(nmd)，而n次排序操作的时间复杂度为O(nmlogm)。然而穷举式kNN算法具有高度的并行特性，即各点的距离计算以及排序操作相互独立，能够同时进行，这与GPU的并行计算特性十分吻合，利用GPU实现穷举式kNN算法可以充分利用当前GPU强大的并行计算能力。

2．排序算法

穷举式kNN查询算法的第2步是对距离值进行排序。对于点云数据，kNN查询只关心前k个最小的距离值，而一般情况下k值远远小于参考点个数m。基于这一点，本文使用了一种适合于GPU实现的排序算法——改进的插入排序算法。

插入排序算法是一种简单直观的排序算法，其基本思想是将一个元素插入到已排好序的有序表中，从而得到一个新的、元素数量增一的有序表。为了只获得前k个最小值，本文对基本的插入排序算法做了一些修改，具体实现步骤如下。

1)根据基本的插入排序算法对数列中的前k个元素进行排序。

2)访问数列中的第k+1个元素，从后到前逐个判断其与前k个元素的大小，当找到第1个比其小的元素后，将其插入到该元素之后。

3)遍历第k+1个元素之后的所有元素，重复步骤2)。

改进的插入排序算法易于实现，当k值较小时能获得较快的查询速度。

3．CUDA实现

鉴于该查询算法由距离计算和排序两部分组成，本文将CUDA的实现分为两个阶段(即两个kernels函数)。

1)第1个kernels函数负责大小为m×n的距离矩阵计算。由于各点之间的距离计算完全独立，距离矩阵的计算可完全并行完成，每个线程根据所给的查询点qi和参考点rj独立完成距离计算。

研究发现，MYB基因的表达可受多种非生物胁迫诱导而出现节律性的昼夜变化[39]，如遮光处理会抑制花青素苷合成通路中结构基因的表达，影响花被片着色[40]。光照处理后，‘索邦’花蕾中LhsorMYB12的表达量明显高于黑暗处理，说明该基因的表达受到光照调节。启动子分析结果显示，LhsorMYB12序列上存在多个光响应元件，推测这些光响应元件可能与光照诱导LhsorMYB12表达上调相关。此外，光照处理4 h后 LhsorMYB12的表达量低于处理2 h和8 h时的表达量，说明该基因的表达可能还受到其他因子的调控，其启动子中存在的参与昼夜节律调控的元件可能与LhsorMYB12表达量的变化相关。

2)第2个kernels函数对计算好的距离矩阵进行排序。由于每个查询点的距离排序完全独立，n个查询点各自的排序操作可完全并行完成，每个线程负责一个查询点的距离排序操作。

CUDA程序一般由主机端代码与设备端代码组成，基于CUDA的穷举式kNN查询的实现流程如图3所示。

四、基于外存的kNN查询

海量点云数据一般无法完全导入到内存中，因此只能将大部分数据存入硬盘。针对这一情况有必要设计一种通过CUDA实现的基于外存的kNN查询算法，从而实现海量点云数据高效的 kNN查询。

1．双层查询结构

传统的kNN查询算法为了提高查询效率，往往通过空间层次结构建立，并只考虑查询点周围节点内的采样点，计算它们与查询点的距离。此类算法一般情况下只需要少量计算便可得到最终的结果，具有不错的效率。但对于海量点云，由于其无法将所有的数据都放入内存，过深的层次结构不仅会增加建树时间，还会因节点过多增加磁盘数据访问延迟，从而降低查询效率;而过于简化的层次结构又会增加参与距离计算的采样点个数，同样也会影响查询效率。

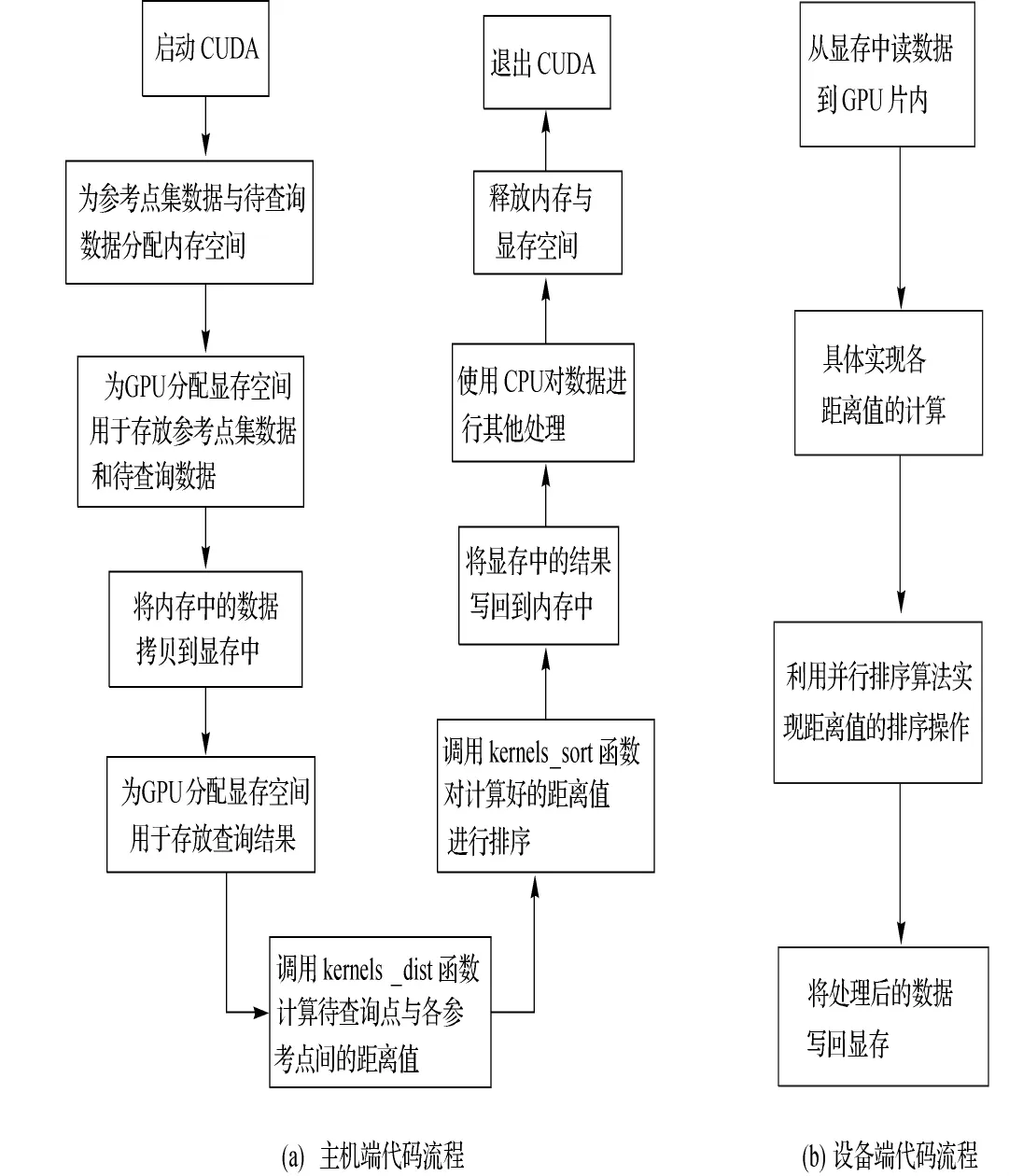
图3 基于CUDA的穷举式kNN查询算法的实现流程

反观基于CUDA的穷举式kNN查询算法，由于其充分利用了GPU强大的并行计算能力，因此其查询效率与传统的查询算法相比优势巨大。然而对于海量点云数据(特别是上千万甚至过亿的点云数据)，单纯依靠该算法同样也会造成巨大的时间消耗，因此需要做相关改进。

通过以上分析不难发现单纯依靠GPU或单纯依靠空间层次结构都不能较好的实现海量点云数据的高效kNN查询，因此本文将这两种方法进行有机结合，提出了一种双层查询结构。基本做法为：对整个点云数据进行遍历，以较大的划分阈值建立空间层级结构，其中阈值可根据点云数据量的大小确定(对于5000万的点云，阈值大小可设为100万)。在查询时只需要进行少量的节点访问便能获得要进行距离计算的节点，然后根据穷举式kNN查询算法，利用GPU强大的并行计算能力对这些节点中的采样点进行邻域计算，快速获得最近邻域点，从而完成整个查询操作。

2．具体实现

对于通过空间划分获得的，且具有显式层次信息的点云多分辨率层次结构，在进行查询时首先对该结构进行遍历，确定查询点所处叶子节点;然后利用穷举式kNN查询算法找到该叶子节点中与查询点最近邻的点。具体流程如下。

1)对于某个查询点首先访问层次结构的根节点，计算查询点到根节点包围盒的距离，并将其放入到节点包围盒队列(pqBoxes)中。

2)从pqBoxes中弹出第1个元素并对其进行访问(第1次访问时为根节点)，遍历其所有子节点，计算它们的包围盒与查询点间的距离，然后逐个加入到pqBoxes中。

4)当pqKNN不为空后，判断其最小距离值(对应的队列元素记为pqKNN．top)是否小于pqBoxes中的最小距离值，如果是，则pqKNN中的最小距离值所对应的采样点就是当前情况下的最近邻点;如果不是，则继续遍历pqBoxes中的元素，重复步骤3)和步骤4)。

5)对于第2个查询点，首先判断其是否处于pqBoxes所维护的各个节点中，如果是，则只需重新计算查询点与各节点间的距离并重新放入pqBoxes中，然后重复步骤3)和步骤4)即可;如果不是，则得首先访问根节点，重复步骤1)～步骤4)。

五、试验与分析

本节将根据上文提出的算法设计相关试验，通过对比分析验证算法的有效性。试验平台基本性能如下：Intel Core2 Q8200处理器(频率2．33GHz)，3GB DDRⅡ内存，GeForce 9800 GT显卡。试验数据为实际采集数据，具体信息如表1所示。

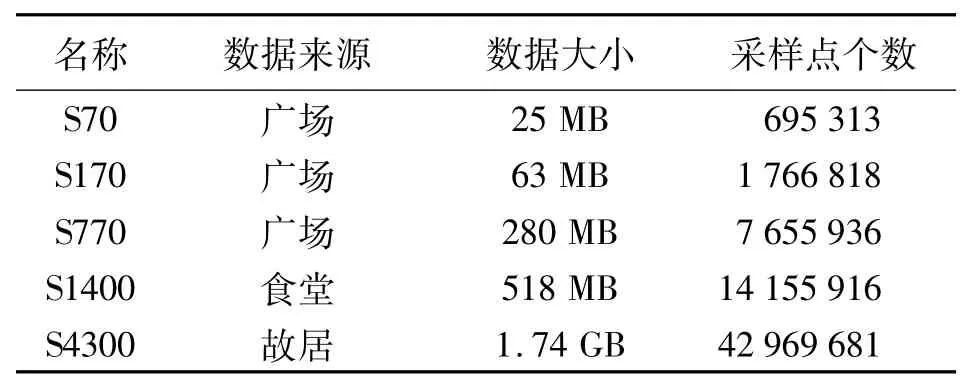
表1 实际采集数据相关信息

1)试验1为基于CUDA的穷举式kNN查询算法与ANN[1]查询算法在查询效率方面的比较。其是基于内存实现的，即所有数据都导入内存，对比试验结果(k=20)如表2所示。

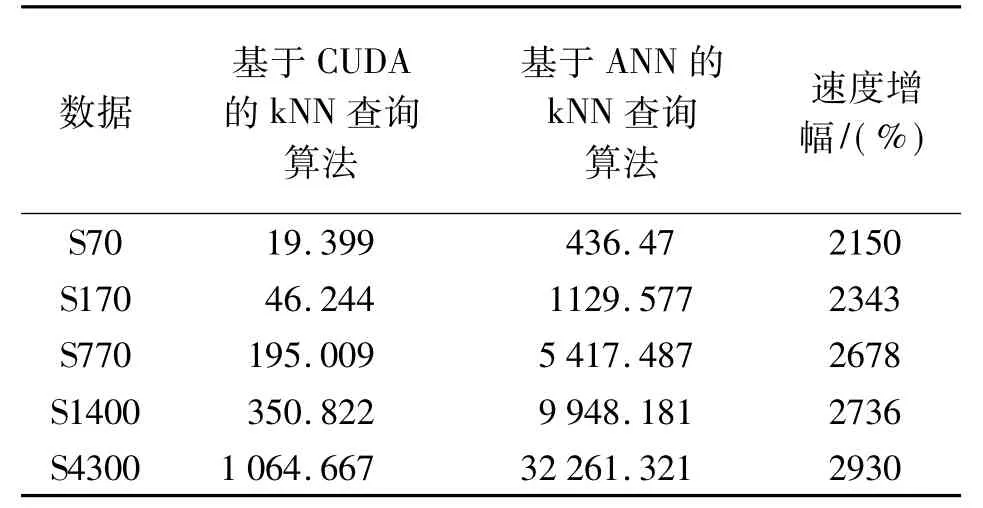
表2 穷举式kNN查询算法与ANN查询算法的试验结果对比 ms

试验结果表明：当所有数据全部导入到内存后，基于CUDA的kNN算法的查询速度较基于ANN的kNN算法有大幅提升，特别是当数据量较大时，查询速度增幅显著。

2)试验2基于CUDA的双层查询算法与普通的基于外存查询算法在查询效率上的比较。其主要针对海量点云数据的kNN查询。改进的双层查询算法与基本算法的区别在于：在kNN查询的第2阶段，改进算法是利用基于CUDA的穷举式kNN查询算法获得叶子节点中的k个最近邻点;而基本算法是利用ANN类库来实现k最近邻域查询。当nmax为65 536，k为20时，对比试验结果如表3所示。

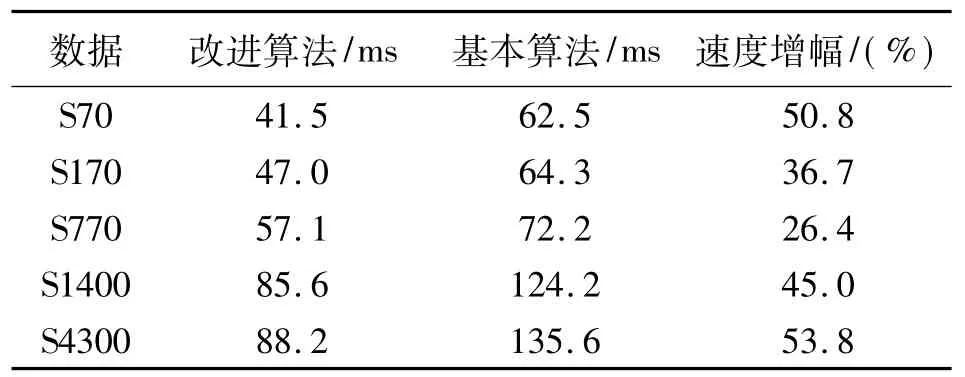
表3 基本kNN查询算法与改进查询算法的实验结果对比ms

试验结果表明：本文提出的改进算法较基本算法在查询速度上有所提升，但增幅较试验1有明显下降。究其原因主要是频繁的数据调度产生了较大的访问延迟，其对查询速度的影响已经成为制约kNN查询效率的首要影响因素。

在基于外存的kNN查询算法中，节点大小是查询效率的重要影响因子，以下试验展示了不同节点大小(即不同的nmax值)对kNN查询效率的影响。如图4所示。

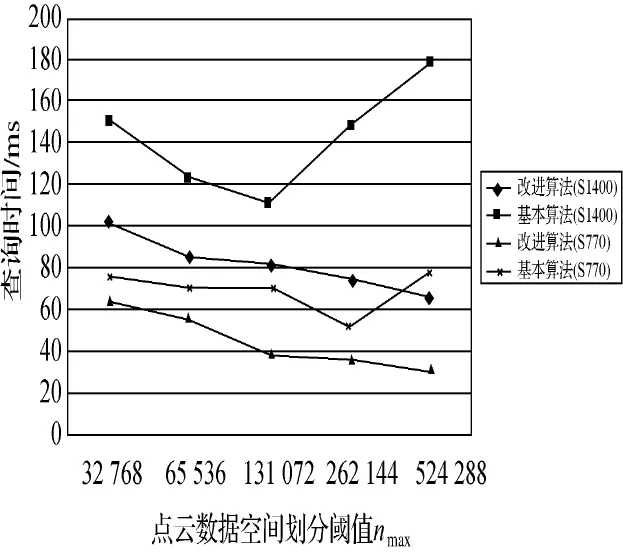
图4 不同节点大小对kNN查询效率的影响

试验结果表明：对于基本算法，其查询时间在开始阶段随nmax值的增大逐渐减少，当达到某个值后开始反向增加;而对于改进算法，其查询时间随着nmax值的增大持续减少。究其原因主要是改进算法所使用的基于CUDA的kNN查询算法较一般的层次查询算法在查询速度上有明显提升，这使得对于较大的nmax值该算法仍能获得较快的查询速度，而此时层级结构的深度较小，节点数据的访问次数相对较少，访问延迟有所降低，从而提高了查询效率。值得注意的是，改进算法的查询时间也并非一直减少，在nmax值增大过程中也会出现一个最小值。所以，在进行kNN查询时应当根据点云数据的实际情况选择合适的划分阈值。

六、结束语

本文根据点云数据的特点以及当前GPU硬件的特性，提出了一种通过CUDA实现的穷举式kNN查询算法。然后将该算法与传统的层次查询算法相结合，设计了一种基于外存的双层查询结构，从而实现了海量点云数据的快速kNN查询。试验证明，笔者的方法与传统算法相比在效率上有明显提升，其为海量点云数据的后处理工作奠定了较好的基础。然而，本文提出的穷举式kNN查询算法虽然充分利用了GPU强大的并行计算能力，但是其算法自身的时间复杂度过高，当点云数据量过大时其查询效率显著下降。因此，在今后的工作中有必要设计一种时间复杂度更低的并行查询算法，以实现更为高效的kNN查询。

[1]ARYA S，MOUNT D M，NETANYAHU N S．An Optimal Algorithm for Approximate Nearest Neighbor Searching[J]．Journal of the ACM，1998，45(6)：891-923．

[2]CEDERMAN D，TSIGAS P．GPU-quicksort：A Practical Quicksort Algorithm for Graphics Processors[C]∥Proceedings of the 16th Annual European Symposium on Algorithms．New York：[s．n．]，2008：246-258．

[3]CLARKSON K L．Fast Algorithm for the all Nearest Neighbors Problem[C]∥Proceedings of IEEE symposium on foundations of computer science．[S．l．]：Gengaga Learning Business Press，1983：226-232．

[4]GARCIA V，DEBREUVE E，BARLAUDM．Fast k Nearest Neighbor Search Using Gpu[C]∥Proceedings of IEEE computer society conference on CVPR．[S．l．]：[s．n．]，2008：1107-1112．

[5]ROUSSOPOULOS N，KELLEY S，VINCENT F．Nearest Neighbor Queries[C]∥Proceedings of the ACM SIGMOD conference．New York：[s．n．]，1995：71-79．

[6]SANKARANARAYANAN J，SAMET H，VARSHNEY A．A Fast All Nearest Neighbor Algorithm for Applications Involving Large Point-clouds[J]．Computers ＆ Graphics，2007，31(2)：157-174．

[7]丁鹏．基于 GPU的通用并行计算库的设计与研究[D]．成都：西南石油大学，2007．

[8]黄淼，张海朝，李超．基于八叉树空间分割的k近邻搜索算 法[J]．计 算 机 应 用，2008，28(8)：2046-2048，2051．

[9]张舒，褚艳利．GPU高性能计算之CUDA[M]．北京：中国水利水电出版社，2009．