横切透视椭圆柱投影在高斯投影教学中的应用
过家春
(安徽农业大学理学院,安徽合肥230036)
一、引 言
文献[1]首先指出有些测量和制图书籍中把高斯-克吕格投影(以下简称高斯投影)与横切透视圆柱投影(以下简称横透投影)混为一谈,有些测绘工作者也有这方面的模糊认识。为此,文献[1]详细论述了高斯投影的推导过程,并推导了横透投影的公式,且对两种投影的异同进行了比较。稍有不足的是,该文首先将高斯投影的公式简化成球体模型下的近似形式,然后在将地球视为球体的条件下推导出横透投影的公式,并与高斯投影进行对比分析,因此高斯投影与横透投影的本质区别没有能够完全体现出来。
尽管横透投影实用性意义不大[1],但事实上地图投影的概念起源于几何透视投影[2-3],各种有关地图投影的学术著作在论述高斯投影、横轴墨卡托投影(UTM投影)等投影时,也经常以透视投影为引例,以建立对地图投影的感性认识[2,4]。由于高斯投影是按一定的投影条件、采用数学分析方法建立起来的条件投影,而非几何透视投影[5-6],对于初学者十分抽象难懂。所以,在高斯投影的教学工作中,常用横透投影来做形象比喻,以帮助初学者理解高斯投影,改善教学效果。但高斯投影与横透投影是完全不同的两种投影。
本文在文献[1]的基础上,基于旋转椭球模型,推导出横透投影的公式,并与高斯投影进行分析比较,以资参考。
二、横切透视椭圆柱投影的公式推导
如图1所示,假想一个椭圆柱横套在地球椭球外面(旋转椭球,记其长半轴为a,短半轴为b,第一偏心率,并与某一经度为L0的子午线相切。类似于高斯投影,称其为横透投影的中央子午线。现假定椭球球心o有一点光源(即设椭球球心为视点),点光源发射直线光束,将中央子午线东西两侧一定经差范围内的地区透射到椭圆柱面上。然后再沿过极点的母线将椭圆柱面展开成平面,建立如图1所示的平面直角坐标系O-XY,即得横透投影。
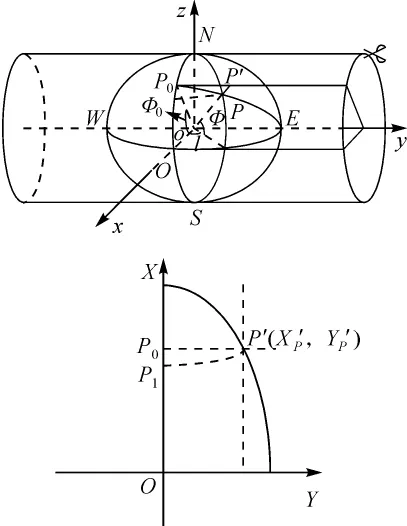
图1 横切透视椭圆柱投影
设图1中P点为距中央子午线一定经差范围内地球椭球上任意一点,其大地经度为L,距中央子午线经差为l=L-L0;大地纬度为B,对应的地心纬度为Φ,二者之间的关系为
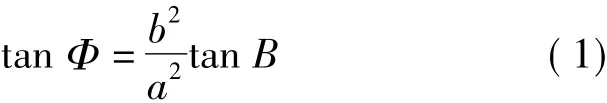
以地球椭球的球心o为坐标原点,建立如图1所示的空间直角坐标系o-xyz,则由椭圆柱及直线oP的方程构成方程组
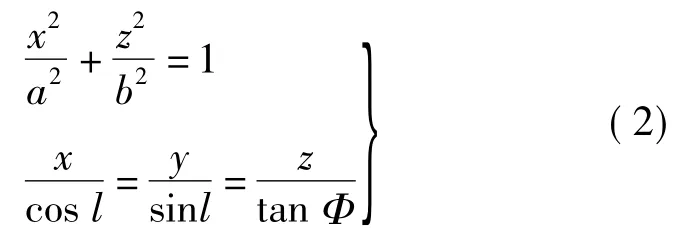
由式(1)及式(2),可得P点在椭圆柱上的投影P'点的空间直角坐标
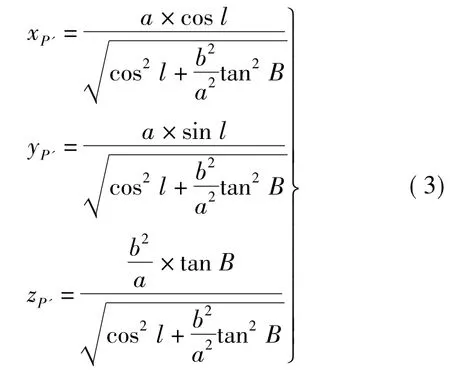
过P'点作中央子午线NOS的垂线,垂足为P0。类似于高斯投影,称P0点大地纬度B0为P'点的底点纬度,对应的地心纬度为Φ0。由图1所示关系有
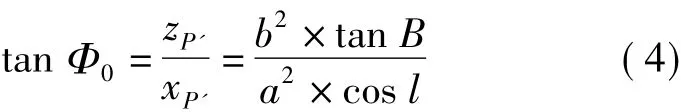
顾及式(1),则得

设P点的投影P'点的平面直角坐标为( XP',YP'),根据以上分析有

式(6)即为旋转椭球模型下的横透投影公式。
三、横切透视椭圆柱投影与高斯-克吕格投影的对比分析
以克拉索夫斯基椭球参数为例,按式(6)计算3°分带的横透投影坐标值,绘制投影后的经纬网,并与高斯投影作比较,结果如表1及图2所示。
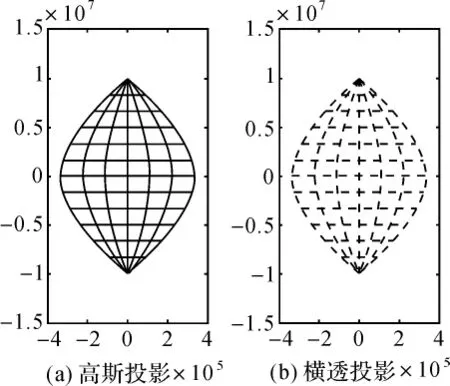
图2 高斯投影与横透投影的经纬网形状
比较横透投影与高斯投影的坐标差值及经纬网形状,可见横透投影的长度变形特征与高斯投影类似,中央子午线和赤道投影后均为直线,且相互垂直,除中央子午线外,投影长度比均大于1,投影后的经纬网形状十分接近。但表1显示,横透投影的纵坐标值比高斯投影略小,横坐标值比高斯投影偏大。可以证明,横透投影为任意投影,其长度、角度及面积均有变形。
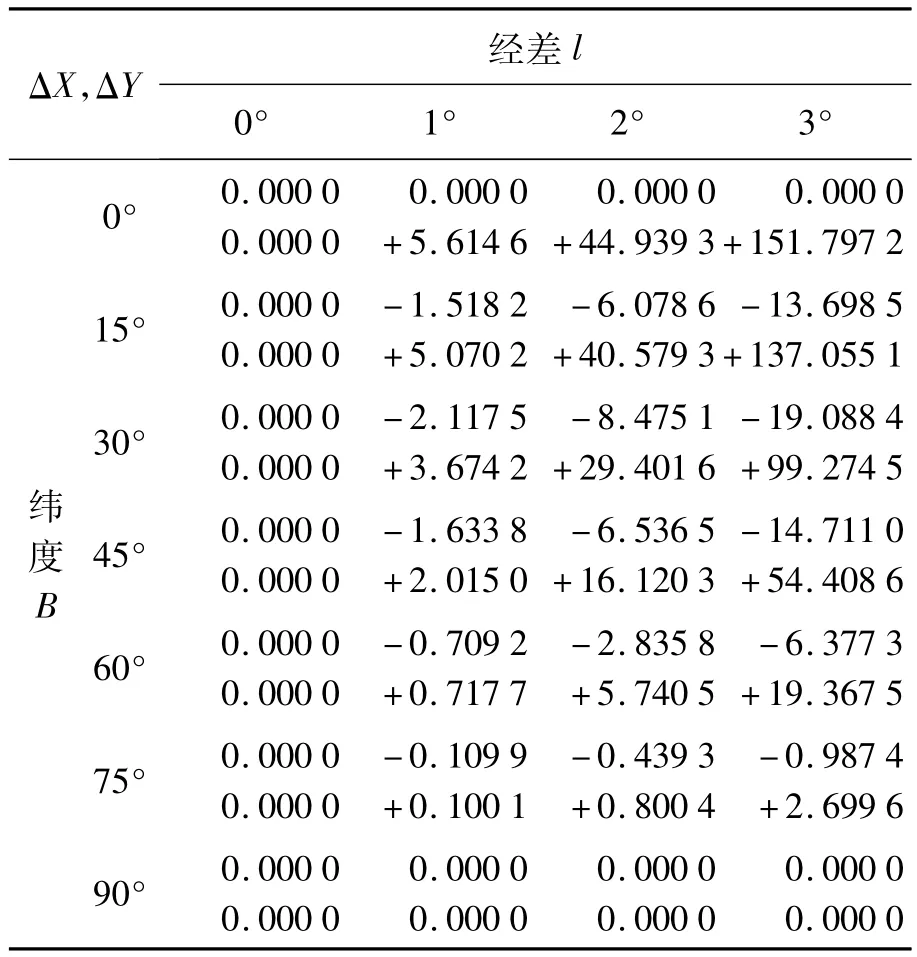
表1 横透投影与高斯投影坐标差值表
四、结束语
综合以上分析可知,横透投影是一种按几何透视原理建立起来的简单投影,几部满足等角投影条件,也不满足等距条件,在测绘科学领域实用性不大。但在高斯投影的教学过程中,尤其是对于非测绘类专业学生的教学,笔者常引导学生思考横透投影的建立过程,以建立起对地图投影的感性认识。实践证明这有利于加深初学者对高斯投影的理解,也激发了学生的学习兴趣。
[1]王政梅.高斯-克吕格投影与横切圆柱透视投影的比较[J].测绘通报,2002(3):11-12.
[2]祝国瑞.地图学[M].武汉:武汉大学出版社,2004:36-37.
[3]SNYDER JP.Map Projections—A Working Manual[M].USGPO:[s.n.],1987:1-4.
[4]吴忠性.地图投影[M].北京:测绘出版社,1978:80-81.
[5]孔祥元,梅是义.控制测量学(下册)[M].武汉:武汉测绘科技大学出版社,1998:38-53.

