小波神经网络在拦渣坝变形预测中的应用研究

李 超，王腾军

(1．长安大学地质工程与测绘学院，陕西 西安710054;2．渭南职业技术学院，陕西渭南714000)

一、引 言

伴随着我国经济的快速发展，各种大型工程开工建设，在施工和生产运行中会产生大量的弃土、弃石、弃渣以及尾矿等废弃固体物质。为了确保各种废弃物的安全放置，保证工程施工和生产运行的安全，必须建立适宜的拦渣坝，它的建立对工程建设意义重大。

但是，随着拦渣坝运行时间的推移，拦渣坝运行的各种条件(如结构、基础、环境等)逐渐发生变化，使得坝体材料老化变质、坝体结构性能衰减甚至恶化等影响其安全运行[1]，这样不仅影响了工程的施工和运行，而且还严重威胁着周边人民的生命和财产安全，这在国内外均有着深刻教训。因此，必须对拦渣坝进行安全监测，建立正确有效的变形预测模型，科学地分析和预测拦渣坝的变形，及时发现存在的安全隐患，制定合理的防治措施，以确保拦渣坝的安全运行，为祖国的经济建设和人民生活水平的提高作出贡献[2]。

由于各种条件和环境的复杂性，使得拦渣坝变形的影响因素存在多样性。通过在许多工程中的应用，发现只利用单一的理论方法(或模型)来对工程变形进行预测，其变形的大小是难以准确预测的[3]。将多种理论和方法进行有机结合，建立一种方法预测工程变形的大小是一种有效的途径[4]。本文基于这样的思想，将小波分析与神经网络有机结合的小波神经网络应用于大型拦渣坝工程实例，建立拦渣坝变形预测模型，对其变形进行了预测。

二、小波神经网络模型

小波神经网络是将小波分析与人工神经网络有机结合的产物。其基本思想是用小波元代替神经元，用已定位的小波函数代替Sigmoid函数作为激活函数，然后通过仿射变换建立起小波变换与神经网络系数之间的连接[5]。小波神经网络结合了小波变换良好的时频局域化性质和神经网络的自学习功能，因而其具有较强的网络逼近能力和容错能力。

目前，将小波分析与人工神经网络的结合主要有下面两种方式[6]：松散性结合，即将小波分析与人工神经网络进行辅助式结合;紧致性结合，即将小波和神经网络直接融合的一种方式，它主要是用小波元代替神经元，将相应的输入层到隐层的权值及隐层阈值分别由小波函数的尺度与平移参数所代替。其中紧致性结合方式也是当前研究小波神经网络模型最主要的结构形式，它也是本文研究的结构形式，其结构如图1所示。

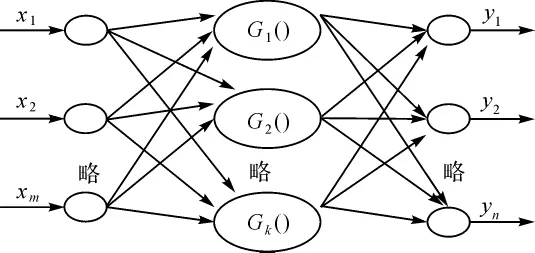
图1 小波神经网络结构图

小波神经网络是在小波分析的基础上提出的前馈型神经网络[7]。可以使网络从根本上避免局部最优并加快了收敛速度，具有很强的学习和泛化能力。小波神经网络激活函数是具有良好时频局域化性质的小波基函数[8]。

设小波神经网络有m个输入节点、N个输出层、n个隐含层节点。并设xk为输入层的第k个输入样本，yi为输入层的第i个输出值，wij为连接输出层节点i和隐含层节点j的权值，wjk为连接隐含层节点j和输入层节点k的权值。约定wi0是第j个输出层节点阈值，wj0是第j个隐含层节点阈值，aj和bj分别为第j个隐含层节点的伸缩和平移因子，则小波神经网络模型可以表示为

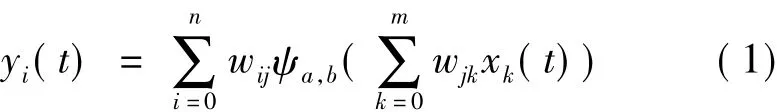
式中，i=1，2，…，N。

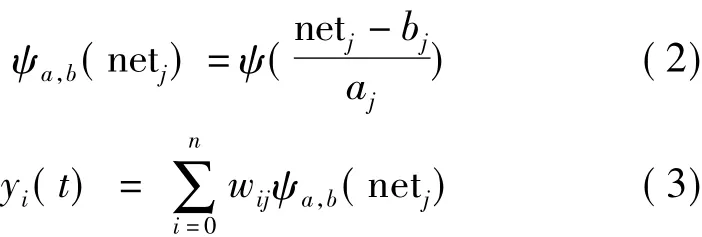
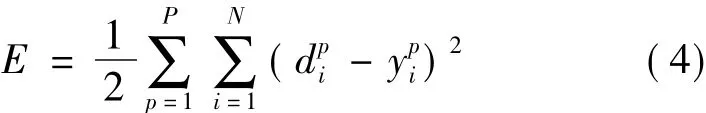
由上面的公式可以计算得到下面的偏导数

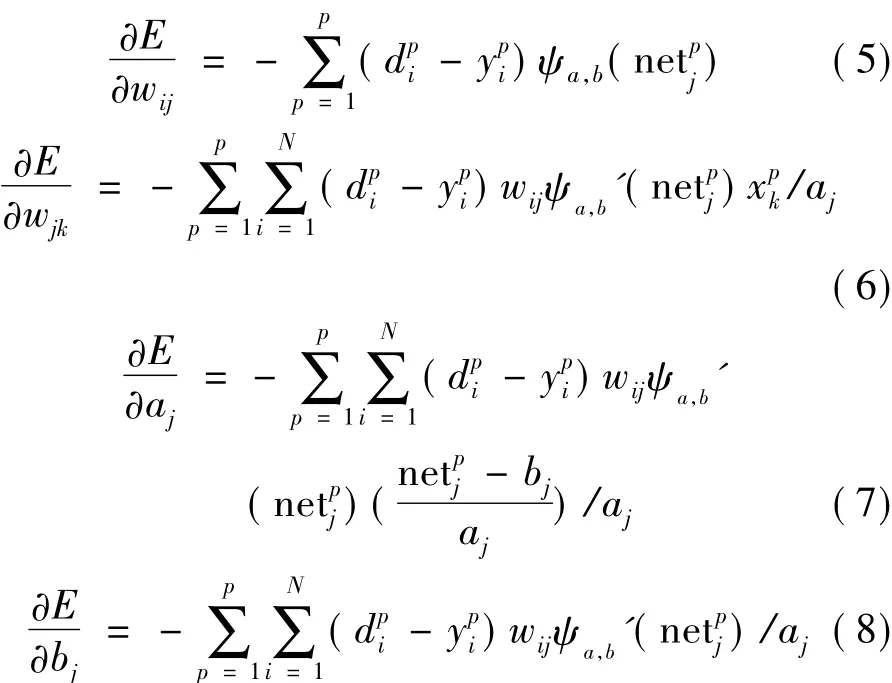
为了加快本算法的收敛速度，参照神经网络引入动量因子α，因此网络按照如下公式迭代公式进行调整，得

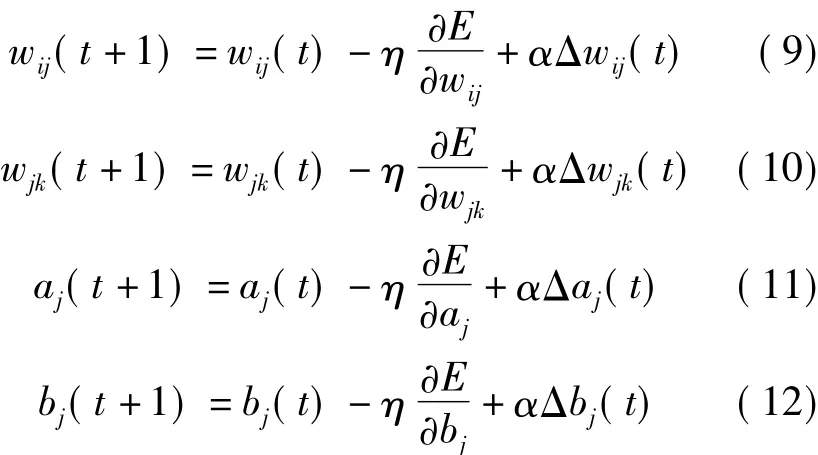
三、拦渣坝工程实例应用

国家重点高速公路杭州至兰州线重庆奉节至云阳高速公路第B4合同段内某拦渣坝，其坝体为混凝土重力坝，长约122 m，高约30 m，拦渣坝上面(上游)是巨大的高速路高填方路基，这在国内是比较罕见的，而下游是梅西河。本拦渣坝主要是为了防止高速路隧道挖方土回填的高填方路基滑动和垮塌发生危险，从而对高速路的运行和梅溪河的通航造成不必要的影响。本文通过对拦渣坝体上S5号点上的沉降监测数据进行分析，建立变形预测的小波神经网络模型。将从2008-09-02—2009-11-05共11期数据作为学习样本对拦渣坝小波神经网络进行训练和学习。对S5号从2010-02-01—2010-12-29共5期数据进行预测。

通过对混凝土坝的研究和本拦渣坝功能作用的分析可知，影响本拦渣坝沉降变化的因素主要有：温度、土压力、时效。其中取4个温度因子[9]，分别为 C、C5、C15、C30(Ci为自观测日起前 i天的平均气温);土压力因子1个(为S5号点附近土压力盒的每期平均计算压力);时效因子2个，分别为T、In T(T为观测日到起算日的累计天数除以100)。故输入层节点数为7个。而输出层节点数为1个，即为观测点S5每次垂直方向的累计沉降量。本文先用经验公式确定一个初始节点数，然后进行试验训练，当隐含层节点数为13时网络训练最为合适，所以本文的小波神经网络模型采用7-13-1的结构形式。通过对不同小波函数的试验训练，多次计算表明，当选用Morlet小波函数时网络的总体性能较好。利用Matlab7．1语言编制相应的网络模型程序进行计算。

为了充分分析小波神经网络的训练效果，本文中也采用相同结构的BP神经网络对拦渣坝监测数据进行训练、预测。在本实例中，设两种模型的收敛误差都取0．000 1。训练结果表明，两种模型的收敛速度都比较快，BP神经网络训练了25次就低于误差限差;而小波神经网络只训练了5次就低于误差限差0．000 1，总体上小波神经网络比BP网络精度高。小波神经网络训练与BP神经网络训练拟合残差系统比较结果见表1。

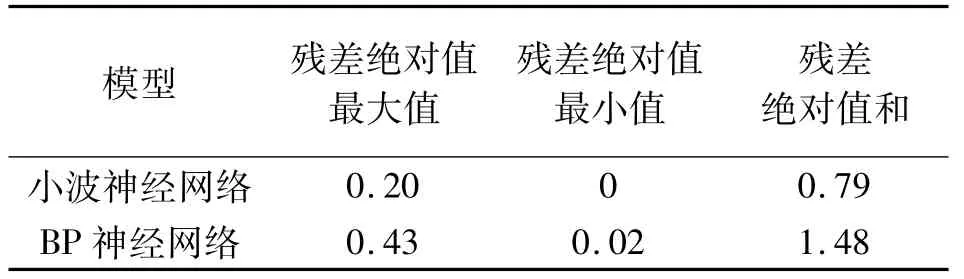
表1 小波神经网络训练与BP神经网络训练拟合残差比较 mm

用所训练好的小波神经网络和BP神经网络对拦渣坝S5号点从2010-02-01—2010-12-29共5期数据进行预测，得到的预测结果见表2。

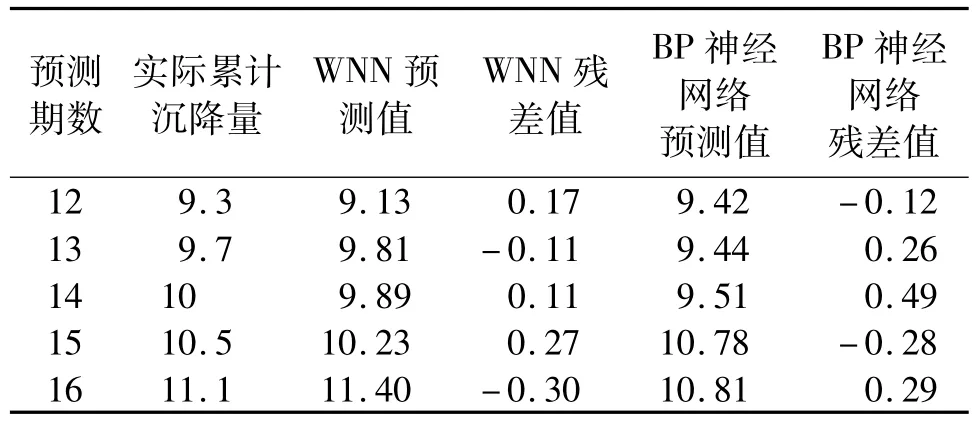
表2 WNN预测结果与BP网络预测结果对比分析 mm

从预测结果对比分析表可以看出，小波神经网络和BP神经网络对拦渣坝变形预测的预测残差绝对值在一个数量级上，但是WNN网络的预测残差值总体上明显小于BP神经网络。小波神经网络的预测值与BP神经网络的预测值相比较更加接近于实际值，WNN预测结果好于BP神经网络预测结果，其预测优越性是显而易见的，小波神经网络与BP神经网络预测对比图如图2所示。

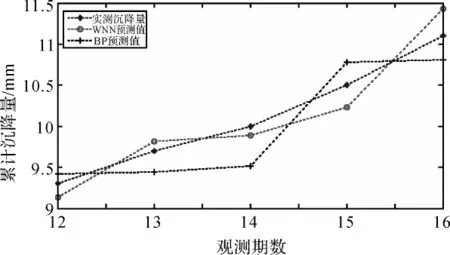
图2 WNN网络与BP神经网络预测对比图

四、结束语

本文通过对小波神经网络模型的研究，建立了拦渣坝变形预测的小波神经网络模型。通过对WNN网络模型和BP神经网络模型训练拟合结果与预测结果的对比分析，可以看出小波神经网络模型在拦渣坝变形预测中的收敛性和精度比BP神经网络好，对拦渣坝的变形预测研究有一定的参考应用价值。

[1]潘国荣，谷川．形变监测数据组合预测[J]．大地测量与地球动力学，2006，26(4)：27-29．

[2]谢国权，戚蓝，曾新华．基于小波和神经网络拱坝变形预测的组合模型研究[J]．武汉大学学报：工学版，2006，39(2)：16-19，27．

[3]黄声享，尹晖，蒋征．变形监测数据处理[M]．武汉：武汉大学出版社，2003．

[4]郎茂祥．预测理论与方法[M]．北京：清华大学出版社，2011．

[5]张正禄，黄全义，文鸿雁，等．工程的变形监测分析与预报[M]．北京：测绘出版社，2007．

[6]高平，薛桂玉．基于小波网络的大坝变形监测模型与预报[J]．水力学报，2003(7)：107-110．

[7]杨丽．小波理论在大坝变形监测数据分析中的应用研究[D]．西安：西安理工大学，2010．

[8]吴中如．混凝土坝观测物理量的数学模型及其应用[J]．华东水利学院学报，1954(3)：20-25．