基于灰色系统理论的概率积分法参数确定研究

陈俊杰，郭延涛

(河南理工大学测绘与国土信息工程学院，河南焦作454003)

一、引 言

矿山开采沉陷是一个复杂的时间和空间问题，对于开采沉陷的预测而言，由于受实测资料中的误差和现场实测情况多变性等因素的影响[1]，基于有限次的现场实测资料和矿区地质采矿条件，很难较为准确地求取概率积分法参数。而灰色系统理论研究对象主要是针对那些“贫信息”、“小样本”的系统，通过对少量表象复杂的原始数据进行挖掘、整理并寻求蕴含在其中的某种整体的内在的变化规律。针对这一特点，可以通过灰色预测来弥补有限次的开采沉陷观测数据带来的不足，更为准确地确定岩层与地表移动参数。

在灰色系统理论应用于开采沉陷的研究方面，李庆勇等建立了灰色系统非等间隔GM(1，1)模型，并将该模型应用于矿山开采沉陷量预测中，证明该模型在矿山开采应用中具有可靠性[2]。苏美德等利用灰色系统理论模拟地表移动的时间过程，求得地表移动的时间响应模型[3]。张东明等针对地表下沉曲线非线性较弱的性质，对地表下沉时间序列进行了探讨[4]。秦晓光等针对高铁路基沉降的特点，发现了灰色系统预测结果更接近于实测值[5]。但总体上，将灰色系统预测理论应用于概率积分法参数的预测与计算方面，尚需做大量的工作。本文基于灰色预测GM(1，1)模型，进行了地表移动变形的概率积分法参数的计算与评价，为研究岩层与地表移动变形规律提供了新的思路与方法。

二、灰色预测模型建立

在求取概率积分法参数时，用灰色预测模型GM(1，1)，其模型的原始形式为[6]

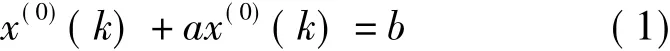
设有原始时间序列为

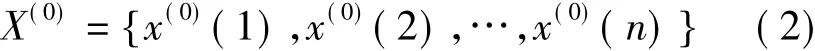
对原始序列进行累加，累加达到r次时，其生成公式为

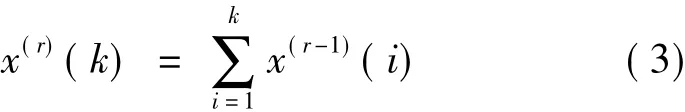
对原始序列进行一次累加，即生成一个新的序列，紧邻均值序列为

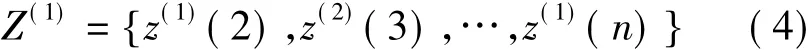
由式(1)、式(4)得，GM(1，1)模型的基本形式为

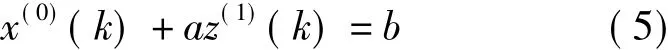
式中，a为发展系数;b为灰色作用量;x(0)(k)为灰导数;z(1)(k)为白化背景值。

由GM(1，1)模型的基本形式可以得到其白化方程为

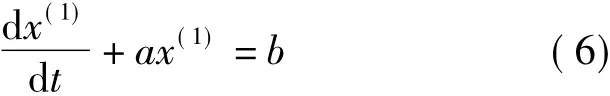
对白化方程进行求解，则得到时间响应函数为

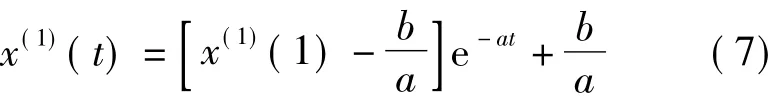
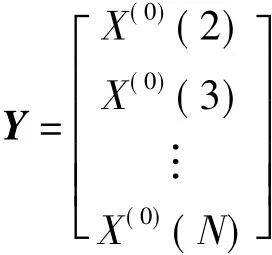
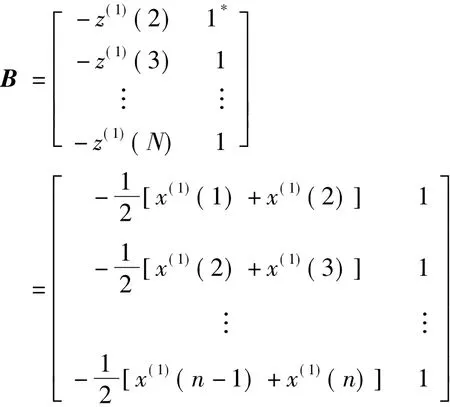
将得到的a、b值代入时间响应函数，即可得到GM(1，1)模型的时间响应公式为

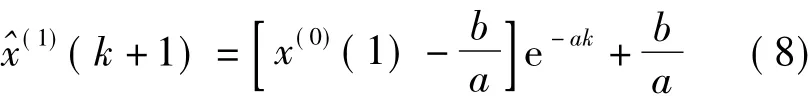
同时，还可得到模型的还原值公式为

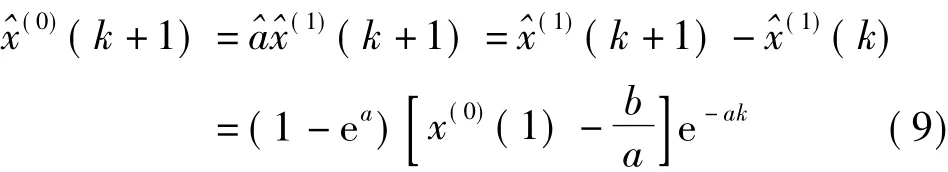
三、研究区概况

潞安矿区司马煤矿位于长治县境内，年设计生产能力150万t，采煤方法为综采放顶煤一次采全高。1101工作面为该矿首采面，长960m，宽165m，采深219m，采厚6．5 ～6．8m，煤层倾角3°～8°。该工作面在回采前，已在地面建立了地表移动观测站。1101工作面于2005年6月开始回采，2006年6月回采结束，平均推进速度为2．67m/d。1101工作面回采后地表出现了明显的下沉盆地，台阶状裂隙发育。在采动影响期间，地表移动观测站进行了多次观测，取得了较为可靠的观测数据。其观测时间见表1。

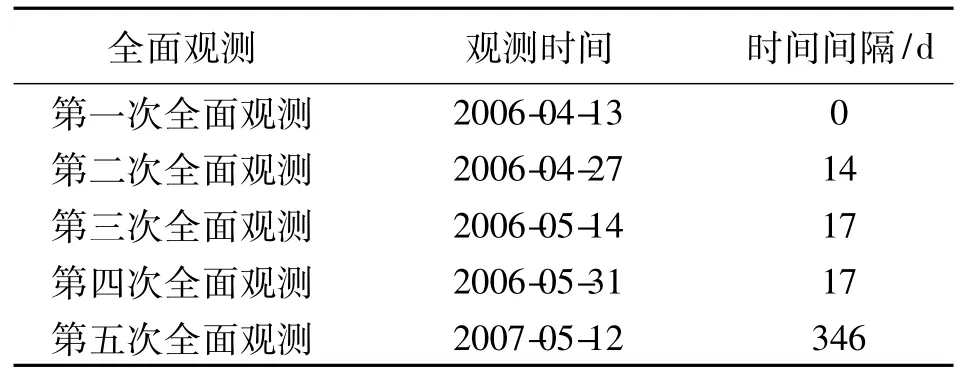
表1 1101工作面地表移动观测站观测时间

四、利用灰色系统理论求取概率积分法参数

1．实测数据的线性插值处理

由表1可知，司马矿地表移动观测站的观测数据是不等时间间隔的，而GM(1，1)模型则以等时间间隔(等步长)序列建模。因此，应对实测数据进行插值处理，以获得等时间间隔数据，保证建立准确的预测模型。

在进行地表下沉分析时，考虑到司马矿1101工作面地表移动的初始期约为10 d左右，活跃期约为60 d，衰退期约为360 d，总共约为430～440 d左右。在进行差值处理时，充分考虑地表移动与变形的时间效应，确保概率积分法参数的准确性。

本文利用Matlab强大的数据处理功能，对下沉值和水平移动值进行插值处理，如表2、图1、图2所示。

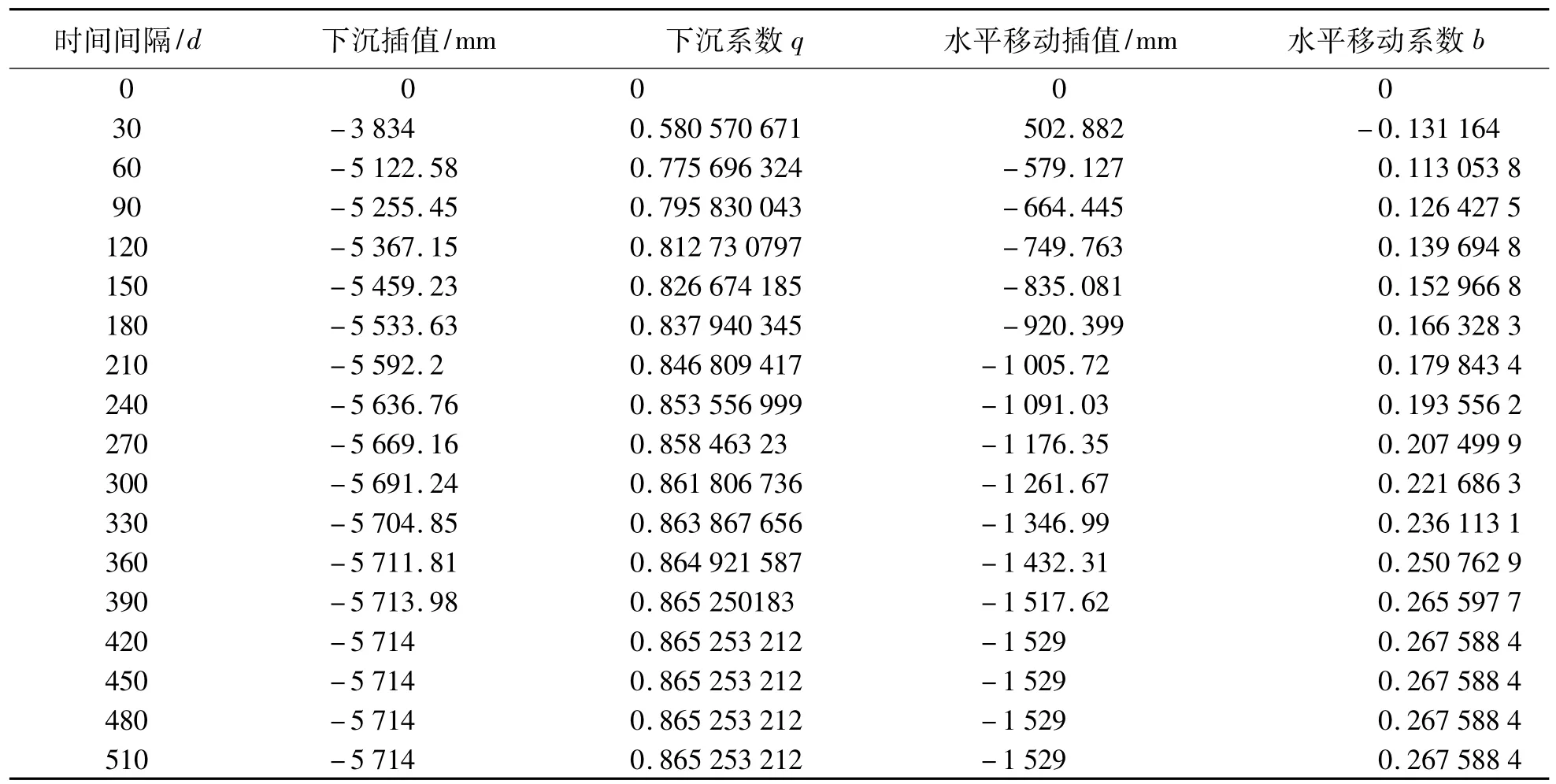
表2 数据的插值处理结果

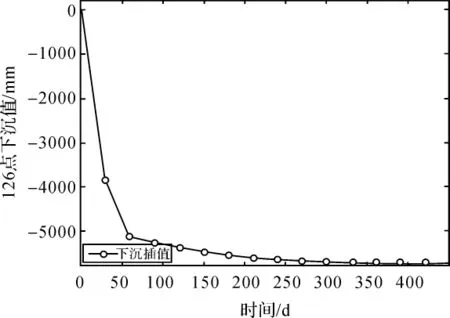
图1 下沉插值分析

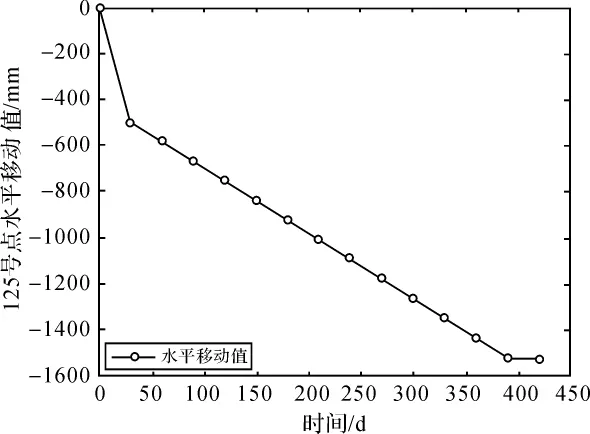
图2 水平移动插值分析

2．概率积分法参数的灰色预测

使用Matlab编写灰色预测及精度检验程序，通过对司马矿1101工作面地表移动观测站的实测数据进行等时间间隔的插值处理，得到等时间间隔的下沉系数q和水平移动系数b序列。通过原始序列的累加或累减，以及紧邻均值序列的计算，根据灰色预测GM(1，1)模型，得到了下沉系数和水平移动系数(见表3)。

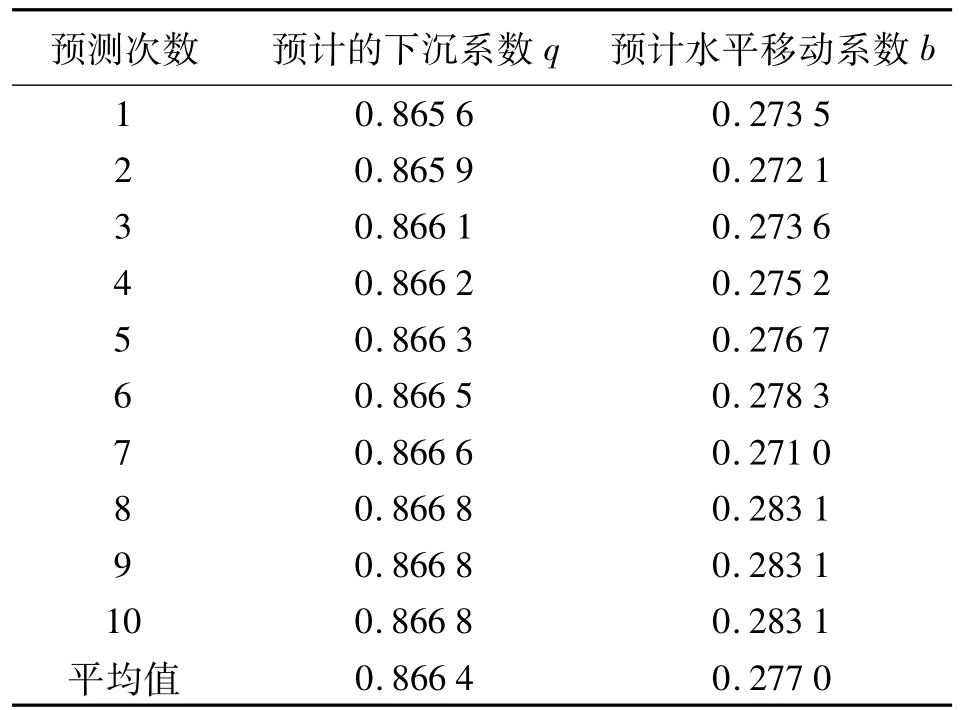
表3 灰色系统预测水平移动系数和下沉系数

由分析可知，通过灰色预测模型得到的地表下沉系数平均相对误差为-0．000 312，残差为0。水平移动系数平均相对误差为0．012 913，残差为0．000 1。二者均满足二级精度的要求[7]。因此，此预测下沉系数GM(1，1)模型是可靠的，其预测结果也是满足要求的。

3．不同预测方法的对比分析

为了检验灰色系统预测模型所得到的概率积分法参数的实用性效果，应用概率积分法数字模型，对地表移动观测站的实测数据进行曲线拟合分析，得到了曲线拟合方法下的概率积分法参数。并与灰色系统预测方法进行对比分析(见表4)。

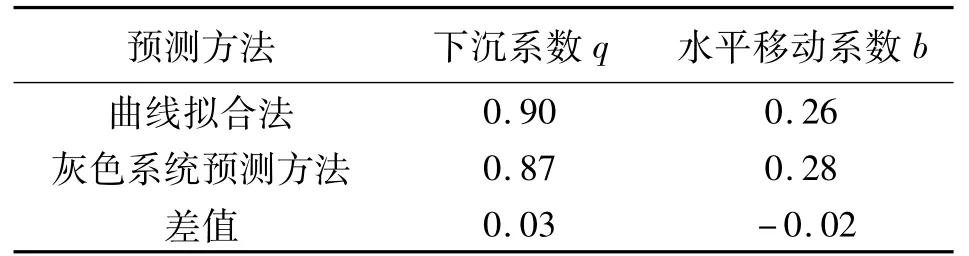
表4 不同预测方法结果对比

从表4可以看出，通过不同预测方法所得到的概率积分法参数，其差值均在0．02～0．03之间，二者存在着一定的误差，原因如下：

1)预计原理不同。曲线拟合法求取概率积分法预计参数是根据实测数据的最大拟合程度来求取的，是对现有数据的分析，是静态的;而灰色系统理论对预计参数的求取是在实测资料的基础上，根据现有数据挖掘出数据序列中的规律，是对未来的分析，是动态的。

2)由于1101工作面地表移动观测站观测数据较少，而灰色系统预测精度则与数据的多少有着密切的联系。现有数据越多，等间隔的观测次数越多，则拟合精度越高，灰色预测结果也越准确，反之亦然。

3)地表移动变形是有时间效应的，存在着初始期、活跃期和衰退期。在初始期和活跃期，地表移动变形变化较快，而在衰退期，地表移动变形趋于稳定，变化较为缓慢。因此，曲线拟合法与灰色系统预测方法存在着误差原因，很大程度上取决于地表移动变形衰退期观测数据的多少与精度的高低。

4)就曲线拟合法与灰色系统预测方法的预计结果而言，均可以有效地为矿区提供技术参数资料，二者得到的预计参数均是可靠的、准确的，其结果在允许的误差范围之内。

五、结 论

1)基于灰色系统预测的等间隔GM(1，1)模型，对地表移动观测站的实测资料进行了线性插值处理，求取了概率积分法参数。

2)对曲线拟合法与灰色系统预测方法求取参数的结果进行了对比分析，指出了二者预测结果存在误差的影响因素。提出可以通过定期等间隔的观测和加大对衰退期的观测次数等措施，提高概率积分法参数的精度。

3)通过灰色系统预测方法求取概率积分法参数的方法是可靠的，并体现了动态预测的特点，可以有效地为矿区“三下”压煤开采提供可靠的技术参数资料。

[1]何国清，杨伦，凌赓娣，等．矿山开采沉陷学[M]．徐州：中国矿业大学出版社，1994．

[2]李庆勇，姚冬青．非等间隔GM(1，1)模型在矿山开采沉陷中的应用[J]．测绘与空间地理信息，2009，32(5)：200-202，205．

[3]苏美德，赵忠明，李德海，等．灰色系统理论模型在矿山开采沉陷中的应用[J]．西部探矿工，2003，15(4)：82-83．

[4]张东明，尹光志，刘见中，等．急倾斜煤层开采地表沉陷的渐近灰色预测[J]．中国地质灾害与防治学报，2004，15(1)：82-85．

[5]秦晓光，杨龙才．灰色预测在高铁路基沉降预测中的应用[J]．华东交通大学学报，2011，28(5)：88-92．

[6]刘思峰，党耀国．灰色系统理论及其应用[M]．5版．北京：科学出版社，2010．

[7]邓聚龙．灰色系统理论教程[M]．武汉：华中理工大学出版社，1990．