GIS图斑面积量算方法及其拓扑判断

严泰来，陈亚婷，刘 哲

(中国农业大学，北京100083)

一、GIS图斑面积量算方法

在地图上，一个用曲线勾划的封闭区域就称为图斑(parcel)，即一个地块。每一个县、乡或村都有边界，用边界围成一个区域就是图斑。对于图斑，人们首先关心其面积，这是任何一个图斑最为基本的地理信息之一。

GIS表现地图的地理信息有两种基本资料数据格式(data format)，即网格格式(grid)和矢量格式(vector)，如图1所示。

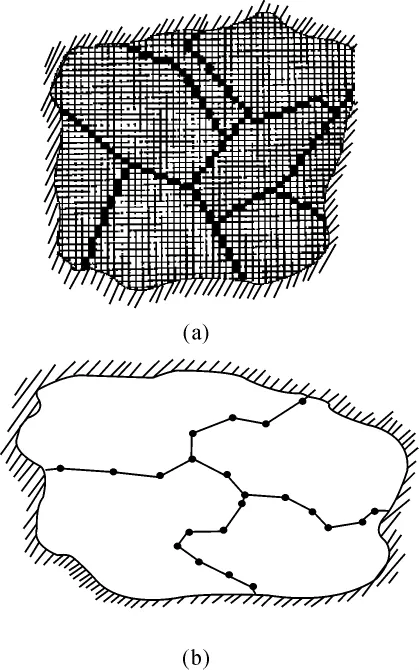
图1 数字化地图数据的网格格式和矢量格式

图1(a)为数字化地图数据的网格格式，所谓网格格式是指用透明、细密、均匀的方格网“覆盖”在地图上，网格有具体的尺寸，网上的每一方格在地图上覆盖的部位具有某一属性，如网格格式表达行政区划图，则各个网格就被赋予对应地图部位的行政编码。当然，有一些网格可能处于两个或三个地块的交界处，此种网格的属性就以分割出最大地块的属性为准。显然，此时图斑的面积A即为属于该图斑的网格数目n乘以一个网格的面积a，即

这种方法简单，但是在GIS中并不常用，原因有两点：①GIS空间数据库基本用矢量格式，网格格式的空间数据库并不多见;②网格格式的精度受制于空间数据库存储量的限制，不能将网格设置过小，所以用这种方法量测图斑面积的精度不高，难以满足实际需要。

图1(b)即为数字化地图数据的矢量格式，所谓矢量格式是指用首尾相接的多条线段链接起来的折线，每一个线段都有方向，用折线逼近曲线的数据表达格式。如果这种折线围成一个封闭区域，就构成一个图斑，于是图斑就变为用有限个线段链接起来的多边形，n个线段链接起来就成为n边形，有n个顶点，每个顶点都有其坐标值(xi，yi)，这里i=1，2，…n。对于这样的多边形，其面积可以用辛普森求积公式计算，见式(2)。

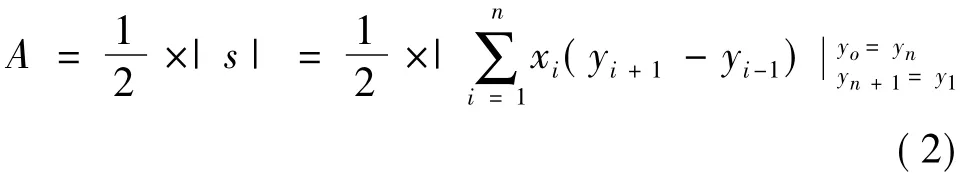
式(2)是用高等数学环积分的思想推导得到，见图2，图2(a)中的阴影部分就是积分的积分单元，是一条线段向y轴投影的面积。这个单元是一个梯形，在已知点(xi，yi)和点(xi+1，yi+1)坐标情况下，该梯形面积可计算，然后将各线段对应的面积单元累加得到积分单元面积的代数和、并经过整理可得到如式(2)所示的辛普森公式，式中用到绝对值符号，这是因为面积没有负值。请注意公式最右端对于y0与yn+1的注解，因为已知点中并没有(x0，y0)与(xn+1，yn+1)这两点。

任何图斑都是一个边界封闭的图形，任何一段线段向y坐标轴的投影总会与另一条或多条线段向y坐标轴的投影重叠，而且单元面积的代数和就留下图斑这一线段条带在图斑内的面积，以图2(b)为例，在d－d+条带中，就有6个线段阴影条带重叠，其代数和就留下多边形内部的区域。这样，所有线段向y坐标轴的投影的阴影面积代数和就构成了待测多边形的面积。

在GIS矢量格式空间数据库中，对于每个图斑边界的每个顶点都按照一定顺序存储坐标数据，因此，GIS软件在此基础上能够快速、准确地按照式(2)计算每个图斑的面积。

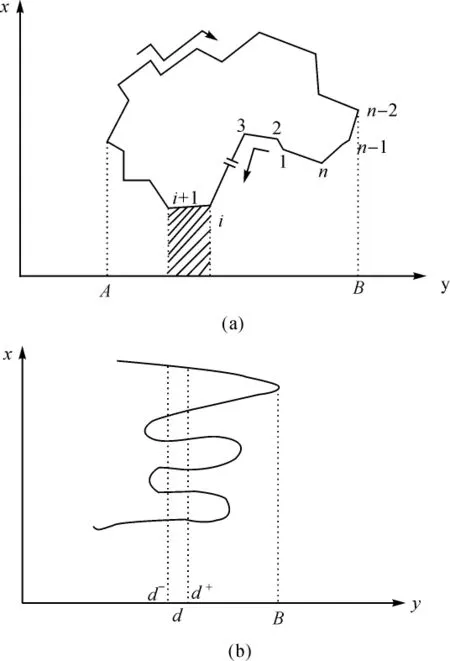
图2 辛普森求积公式原理图

二、GIS基于矢量格式数据测算图斑面积误差的估计

如果一个闭合区域确实是一个真正的多边形，即区域边界是由直线段组成，而且该多边形顶点的坐标资料完全准确，用式(2)计算其面积是没有误差的，因为式(2)是经过严格数学证明的。但是基于矢量格式数据用式(2)测算图斑面积存在误差，问题在于采集用光滑曲线围成的闭合区域坐标存在误差，这里有两种采集误差。

1)布点误差。如图3所示，一般闭合区域边界是一条平滑、自然随机弯曲的曲线，而在这种曲线上采集有限个点，用折线逼近曲线，一定会有误差。比如，在A点处，因布点原因，形成的多边形在这里面积减少了;而在B点处，因布点原因，形成的多边形在这里面积增加了。对于整个区域，因布点带来的正负误差不能完全抵消，就使面积测算最终结果有误差。

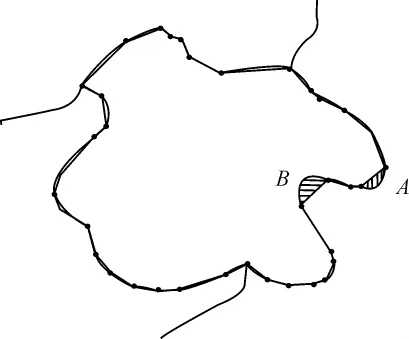
图3 图斑边界采集布点误差示意图

2)采点坐标误差。区域边界严格意义上是没有宽度的，但是实际地图上区域边界总是有宽度的，夸大一点说是一个条带。对地图上区域边界采点，理想位置应当在边界条带的中轴线上，但是人工采点是难以做到的，总会偏离理想位置，这就产生误差。

以上布点误差与采点误差，不可避免地致使测算图斑面积存在误差，相对误差可由式(3)估计

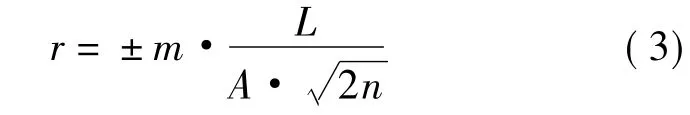
式中，r为面积计算的相对误差;m为多边形边界坐标采点的方差;L为多边形周长;A为多边形面积;n为多边形边界坐标采点的数目。

由式(3)可以看出，面积测算的相对误差与多边形边界坐标采点的方差成正比;与多边形的周长面积比成正比;与采点数目的平方根成反比。这里“周长面积比”这一新概念值得注意，事实上如果一个图形的周长很长、而面积相对很小，自然地表物件，如大坝在河流拦截形成的水库，常常具有这样的特点。由此说明物件图形形状越复杂，面积测算误差就越大。此外，多边形边界坐标采点的数目对面积测算也有重要影响，采点数目越多，面积测算相对误差越小，这是因为随着采点数目的增加，面积测算正负误差相互补偿的概率也在增加，致使相对误差减少。

式(3)适用于估算一个多边形面积的测算误差，也适用于估算一幅数字化地图测算各图斑面积的总体相对误差，此时，L取地图中各多边形周长的平均值;A取各多边形面积的平均值;m经试验得到，通常有一个经验值;n取各多边形边界坐标采点数目的平均值，在GIS软件支持下获取以上数据是不困难的。由此可以看出，地图的图形越复杂，测算各图斑面积的总体误差也就越大。

三、辛普森求积公式法判断点与矢量线的拓扑关系

式(2)所示的辛普森公式有绝对值符号，如果将绝对值符号去掉，由图2可知，在左手坐标系(Y坐标轴横向，向右为正;X坐标轴纵向，向上为正)条件下，多边形顶点坐标按顺时针(如图2所示)排列，则公式计算值为正值;反之，多边形顶点坐标按逆时针排列，则公式计算值为负值。这个性质可以在GIS拓扑判断中使用，如图4所示。辛普森公式适用于计算三角形面积，如图4中的△ABP，计算其面积将顶点坐标代入式(2)则有

图4 拓扑判断原理图

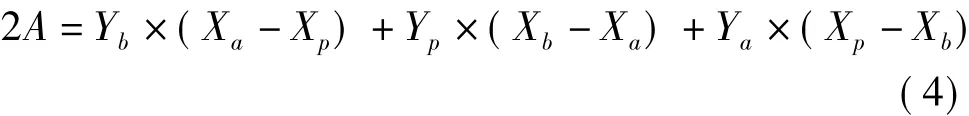
对于A值有3种可能：即A＞0，则△ABP按顺时针方向排列，即点 P在矢量 AB的右面，如图4(a)实线所示;A＜0，则点P'在矢量AB的左面，如图4(a)虚线所示;A=0，则点P在矢量AB的线上。又分以下三种情况：即点P在矢量AB的线段上，如图4(b);点 P在矢量 AB的延长线上，如图4(c);点 P在矢量 AB的反向延长线上，如图4(d)。3种情况归于哪一种，由3点坐标数值关系决定。

这里提到的拓扑(Topology)关系是指空间几何体，包括点与点、线与线、点与线、面与面、点与面、面与线等相互之间的方位关系，在GIS软体运行工作中，有大批量的空间资料需要判断其空间拓扑关系。

四、拓扑判断用于图形特征的提取

多边形在形状上有多种特征，计算机软体可以自动提取这些特征，为识别多边形对应的物件提供线索。这里给出多边形形状特征的一种判断表达方法，见图5。图5所示的多边形是一个凹多边形，其顶点按逆时针方向排列，这可以用以上介绍的辛普森公式

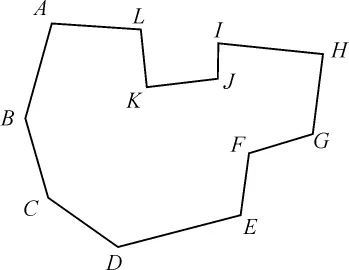
图5 多边形的一种空间特征提取方法

计算面积是负值的结果判断出来。进一步观察可以发现，连续取多边形3个顶点组成三角形，其中，△ABC、△BCD、△CDE、△HIJ、△KLA、△LAB 是逆时针方向排列;而△EFG、△IJK、△JKL 3个三角形是顺时针排列，与整个多边形顶点排列方向逆向。整个多边形的面积可以计算，逆向排列的三角形面积累加和也可计算，两者之比可以作为一个多边形的特征加以定量计算，这个比称之为图形边界的凹凸比。图形边界的凹凸比作为图形特征的一个参数具有实际意义，因为一个物件的影像中难以避免因投影、物件呈现的姿态等多种原因产生种种变形，而物件对应图形边界的凹凸比却变化很小，利用这一特征参数就可能为识别这一物件提供依据。图6显示图形凹凸比特征在昆虫识别中的一个应用。

仔细观察图6可以发现，图6左边蝴蝶包括翅膀在内的身体轮廓凹陷点较少，凹陷较浅，但是左右副翼下面各有一个黑色凸出条带，致使总体上边界的凹凸比指数较大;而右边蝴蝶包括主翼瘦窄，上下主、副翼之间裂隙较深，但是左右副翼边界平滑，没有凸出条带，致使总体上边界的凹凸比指数较小。此外，两个蝴蝶的颜色差异较大，用色度学(Chromatics)原理进行分析，又会发现更多的不同。除了物种形体边界的凹凸比特征指数外，周长面积比也是一个特征指数，经研究还有更多的特征指数，用计算机软体都可以计算提取。

如果在计算机信息系统中带有储存各种昆虫物种的特征指数数据库，对于实际工作采集来的昆虫影像样品计算其形体特征及色调特征，并且与特征指数数据库的资料数据逐一加以比对，就可以判断待判断昆虫物种的归属。对于国家边境口岸的海关人员，识别境外有害昆虫物种十分重要，因为放过带有有害昆虫物种的蔬菜、水果入境，将会造成不可挽回的巨大损失。计算机信息系统辅助判别有害昆虫物种对于保障国家的生态安全、农产品安全具有重大意义。事实上，采用与以上类似算法发展的计算机软件已经应用在各个边防口岸、卫生检疫部门，应用面正在不断扩大。

图6 两种蝴蝶影像图

(略)