不同成像条件下目标纹理特征描述之间的转换方法研究

宇 洁，关泽群

(同济大学测量与地理信息学院，上海200092)

一、引 言

纹理作为物体表面自然属性，是一种反映影像同质现象的视觉特征。对于纹理的研究发展至今已有50余年历史，形成了许多描述不同成像条件下目标纹理特征的方法。在对多光谱影像纹理研究中，Haralick[1]于1973年开创性地提出了如今应用极其广泛的灰度共生矩阵(GLCM)，用以解决在Landsat-1多光谱影像上研究美国加利福尼亚海岸带的土地利用问题;Weszka[2]应用灰度差分统计法对美国肯塔基州东部多光谱影像进行地形研究;随后，马尔科夫随机场(TS-MRF)模型[3]、高斯马尔科夫随机场(GMRF)理论[4]、分形模型[5]、多进制小波[6]等理论也相继在光谱影像的纹理描述领域得到了成功应用。

随着1978年美国第一颗在地球轨道上运行的雷达卫星成功发射，影像纹理的研究进入了一个新阶段。Soh和 Tsatsoulis[7]在 ERS-1的影像上利用GLCM对海洋冰层影像进行纹理分析;Duskunovic[8]等人对美国丹佛SAR影像运用MRF进行纹理分类;胡召玲[9]等人成功借助 Daubechies3正交小波对徐州地区部分Radarsat影像进行了纹理信息提取;倪玲[10]等人采用正交小波和第二代小波对机载SAR影像进行纹理分类，并对不同小波分类结果进行了分析比较。

根据 Tuceryan和 Jain[11]提出的分类准则，以上对不同成像条件下纹理的描述方法可分为5类：统计方法、几何方法、结构方法、模型方法和信号处理方法。其中应用较为广泛的是GLCM和Gabor小波方法。本文对不同成像条件下纹理间转换的研究是在基于Gabor小波纹理描述上展开的。

1989年Mallat[12]首先将小波理论引入图像纹理分析描述中，小波理论便开始在图像纹理分析中得到迅速而广泛的应用，并由其发展出许多分支。其中，Gabor小波已被证实是在2D测不准的情况下对信号空域和频域的最佳描述。Dunn和Higgins[13]使用二维Gabor小波对图像进行分割，并根据已知样本给出了最佳滤波器的设计准则;吴高洪[14]等人根据纹理间Fourier频谱密度，提出了一种在双纹理图像分割时最佳单Gabor滤波器的设计方法;陈洋和王润生[15]将Gabor小波和独立成分分析(ICA)技术结合用于纹理分类;Clausi和 Jernigan[16]在考虑人类视觉系统(HVS)基础上运用Gabor小波滤波器分别对加拿大境内结冰水面SAR影像和Brodatz纹理库中影像进行综合纹理分割。本文中将使用Gabor小波分别对光学影像和SAR影像进行纹理特征提取。

目前，人们对于不同成像条件下纹理间转换方法的研究极少，这方面的资料也相对较少。本文将会对这方面做出相应研究。

二、Gabor小波纹理描述

自20世纪90年代以来，人们就开始尝试使用Gabor滤波器对图像纹理进行描述。Gabor滤波器组具有方向、径向频率带宽及中心频率可调谐的优点，能同时在时、频域达到纹理描述最优。该方法是基于“纹理是窄带信号”理论[17]，根据不同纹理转换到频域时一般具有不同的中心频率、带宽，设计一系列Gabor滤波器对图像进行滤波，每个Gabor滤波器只允许与其频率、方向相对应的纹理顺利通过，而使其他不同类别的纹理能量受到抑制。故当使用Gabor滤波器组对图像滤波后，会生成若干个与滤波器分别对应的滤波结果，即不同类别纹理特征提取结果。

Gabor滤波可看作一种母小波为Gabor函数g(x，y)的小波变换，即

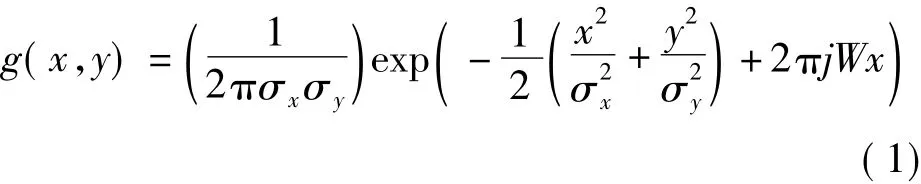
式中，W为高斯函数复调制频率;σx，σy为高斯函数在x轴、y轴的均方差，即信号在空域中x轴、y轴方向上的窗口半径，这两个值决定了高斯函数包络的形状[18]。由式(1)可以看出，Gabor函数实质上是高斯函数调制的正弦波。

通过对g(x，y)进行适当尺度变换和旋转变换，就可得到自相似的一组Gabor滤波器组。

图1 Lena

图2 Lena图像不同方向的纹理图

从结果不难看出，Gabor小波变换可以很好地描述不同方向上图像的纹理特征，满足了人们对不同频率、不同方向纹理研究的需求。

三、基于高斯混合模型(GMM)的异质图像纹理转换

1．GMM原理

近些年来，随着高斯混合模型在语音识别领域的广泛应用，人们开始尝试将其应用于图像处理领域。如Permuter和Francos[19]等人将多尺度小波分析与高斯混合模型相结合，并成功地对彩色纹理图像进行了分割。

根据概率论中的中心极限定理，大量相互独立、服从统一分布的随机变量在总体上服从单高斯分布。故单高斯分布在一维空间中是一种常见的、有效的概率模型，而多个单高斯模型的线性组合(即高斯混合模型)则可以平滑地逼近任意形状的概率密度函数，从而在多维空间中有效地表征一般的概率模型，具有普遍性。

在纹理描述过程中，GMM可以用来拟合不同成像条件下目标纹理特征矢量所具有的概率分布，对特征空间做“软”分类。设纹理图像的像素总数为N，则图像整体概率密度表示为

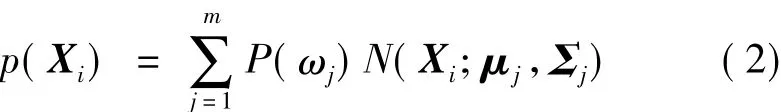
式中，Xi(i=1，2，…，N)为某一成像条件下纹理图像灰度值;m为高斯混合成分的数目;ωj为第j类纹理;P(ωj)表示第j类纹理在整幅纹理图像中的权系数，即第 j类的先验概率;是第 j类纹理的正态分布;是第j类的高斯分布参数，分别表示均值向量和协方差矩阵。当已知纹理图像各像素值时，确定GMM的关键就是求解各类高斯分布参数及权值。

2．高斯混合模型参数求解

目前，在求解高斯混合模型参数的众多方法中使用最为广泛的是EM(Expectation Maximization)。它是一种递归最大似然算法，分为E和M两个步骤，首先获得似然函数期望值，其次再求根据期望值求的对应参数。具体步骤如下：

1)初始化各类高斯分布参数(μj，∑j)和权重P(ωj)，根据贝叶斯理论可以计算某纹理特征向量Xi属于第j类特征的概率，即

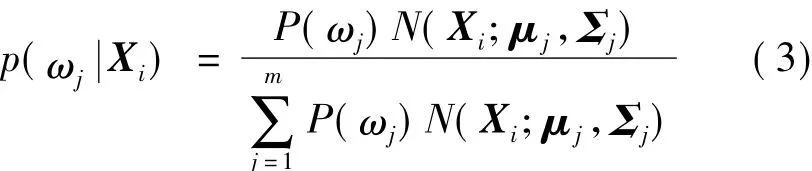
3．转换函数

实现不同成像条件下目标纹理的转换实际上就是建立不同成像条件下纹理间映射的过程。在GMM中，每个单高斯均可表示一类纹理特征，基于GMM的纹理转换就是对某一成像条件下源纹理矢量Xi，根据另一成像条件下目标纹理矢量Yi，求解出相应转换函数F。

设F分段线性，表达式如下

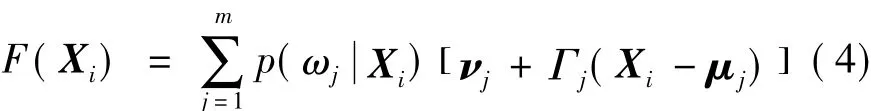
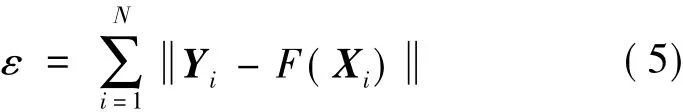
在此基础上Kain[20]等人对求解过程做了一定改进，将Xi和Yi构成联合矢量，通过解算联合矢量Zi的GMM模型得到转换函数最佳形式

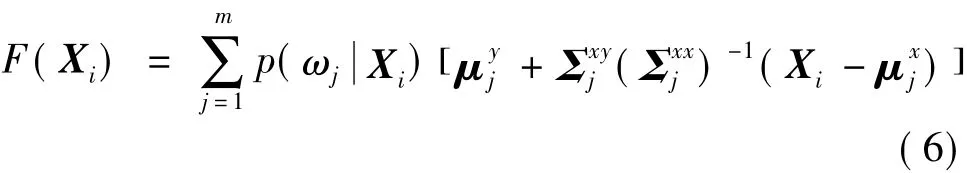
各像素转换结果精度评定采用如下公式

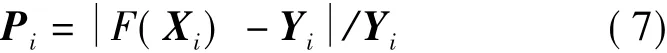
四、试验与分析

本文采用的空间分辨率为1m的同一地区光谱影像和SAR影像已经过严格配准(如图3所示)。首先对两幅影像进行不同方向的Gabor小波纹理描述。

图3 试验采用的影像

经Gabor纹理描述结果可以得知两类影像拥有更明显的横、纵向纹理，故本文选择两幅影像横向(θ=π)纹理分别作为源纹理及目标纹理，并形成转换函数从而建立两者间映射关系。

因试验采用了Kain等人提出的联合矢量算法，该算法是在基于回归的基础上使得GMM模型中混合成分的配置更合理，但在计算过程中增大了计算量。为减少实际计算量，本试验采用如下方法：①在纹理图上截取300×300局部纹理图像作为试验数据，(如图4所示);② 在建立不同成像条件下纹理间映射关系前，先用K均值算法对试验数据进行聚类。

图4 两类影像局部100×100横向纹理

图5为当高斯混合模型混合个数m设置为4时，300×300的局部光谱纹理影像经转后的纹理图，根据式(8)计算得转换误差为0．356 2。为进一步研究基于高斯混合模型的异质图像纹理间转换方法，本文截取其中右下角建筑物区域(如图6所示)，分别对高斯混合模型混合个数m设置为4、8、16及64类，输入源光谱影像纹理后不同m值得到的转换后纹理结果图如图7所示。

图5 经转换后纹理图像

图6 两类影像局部建筑物区域横向纹理

由结果可以看出，转换后的纹理图与目标纹理具有较高的空间相似度及表现形式，如在图7(a)左上角建筑物经转换后与图7(b)中所表达的相似度大大提高，从而证明了基于高斯混合模型建立的不同成像条件下纹理间转换是可行的。

按(7)式计算不同m值下转换结果误差精度平均值，结果如表1所示。

图7 m取不同类时建筑物区域转换结果

表1 不同m值下转换结果误差精度平均值

由表中数据看出，转换精度随着高斯混合数的增加而不断提高。

选取m=64时的试验结果，从中选取50个连续的像元绘制转换前后纹理的相似对比图(如图8所示)，其中X轴表示选取50个像元从1—50编号，Y表示各个像元值。点横线表示50个像元的源光谱纹理值，点实线表示50个像元目标SAR纹理值，星实线则是光谱值通过转换后的转换纹理值。

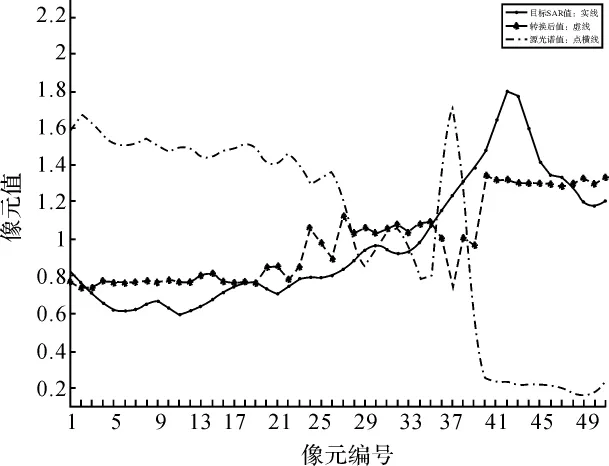
图8 m=64时结果对比曲线图

从图中可以明显看出，转换后结果与目标纹理的吻合度较之源纹理与目标纹理的吻合度要大，从而证明了基于高斯混合模型建立的不同成像条件下纹理间转换是可行的。

五、结束语

利用Gabor滤波器对不同成像条件下同一区域影像进行多方向纹理提取，选取光谱及SAR影像的横向纹理作为源纹理和目标纹理，基于高斯混合模型理论建立源纹理与目标纹理间转换关系并求解转换函数中未知参数，获得最终转换函数。通过试验可以看出，经过转换后的纹理图与目标纹理图具有较高的相似度，并且随着混合模型个数的增加，转换的误差也在不断减小。但试验中计算量会随着混合模型个数的增加而急剧上升，故试验时应选择一个合适的混合模型个数。

[1]HARALICK R M，SHANMUGAM K，DINSTEIN I．Textural Features for Image Classification[J]．IEEE Transactions on Systems，Man，and Cybernetics，1973，3(6)：610-621．

[2]WESZKA JS，DYER CR，ROSENFELD A．A Comparative Study of Texture Measures for Terrain Classification[J]．IEEE Transaction on Systems，Man，and Cybemetics，1976，6(4)：269-285．

[3]LOPEZ-ESPINOZA E D，ALTAMIRANO-ROBLES L．A Method Based on Tree-Structured Markov Random Field and a Texture Energy Function for Classification of Remote Sensing Images[C]Proceeding of 5th International Conference on Electrical Engineering，Computing Science and Automatic Control．Mexico city：[s．n．]，2008：540-544．

[4]CHELLAPPA R，CHATTERJEE S．Classification of Texture Using Gaussian Markov Random Fields[J]．IEEE Transaction on Acoustics，Speech，and Signal Processing，1985，33(4)：959-963．

[5]PENTLAND A P．Fractal-Based Description of Natural Scenes[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6(6)：661-674．

[6]CHITRE Y，Dhawan A P．M-band Wavelet Discrimination of Natural Textures[J]．Pattern Recgnition，1999，32(5)：773-789．

[7]SOH L，TSATSOULIS C．Texture Analysis of SAR Sea Ice Imagery Using Gray Level Cooccurrence Matrices[J]．IEEE Transactions on Geoscience and Remote Sensing，1999，37(2)：780-795．

[8]DUSKUNOVIC I，HEENE G，PHILIPSW，et al I．Urban Area Detection in SAR Imagery Using a New Speckle Reduction Technique and Markov Random Field Texture Classification[C]∥Proceeding of International Geoscience and Remote Sensing Symposium．Honolulu，USA：[s．n．]，2000：636-638．

[9]胡召玲，郭达志，盛业华．基于小波分解的星载SAR图像纹理信息提取[J]．遥感学报，2001，5(6)：424-427．

[10]倪玲，张剑清，姚巍．基于小波的SAR影像纹理分析[J]．武汉大学学报：信息科学版，2004，29(4)：367-370．

[11]TUCERYAN M，JAIN A K．Texture Analysis，Handbook Pattern Recognition and Computer Vision[M]．Singapore：World Scientific，1993：235-276．

[12]MALLAT SG．A Theory for Multiresolution Signal Decomposition：The Wavelet Reprentation[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7)：674-693．

[13]DUNN D，HIGGINSW E，WAKELEY J．Texture Segmentation Using 2D Gabor Elementary Function[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，1994，16(2)：130-149．

[14]吴高洪，章毓晋，林行刚．分割双纹理图像的最佳Gabor滤波器设计方法[J]．电子学报，2001，29(1)：48-50．

[15]陈洋，王润生．结合Gabor滤波器和ICA技术的纹理分类方法[J]．电子学报，2007，35(2)：299-303．

[16]CLAUSID A，JERNIGAN M E．Designing Gabor Flters for Optimal Texture Separability[J]．Pattern Recgnition，2000，33(11)：1835-1849．

[17]BOVIK A，CLARK M，GEISLER W S．Multichannel Texture Analysis Using Localized Spatial Filter[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12(1)：55-73．

[18]李钰，孟祥萍．基于Gabor滤波器的图像纹理提取[J]．长春工业大学学报，2008，29(1)：78-81．

[19]PERMUTER H，FRANCOS J，JERMYN I．A study of Gaussian Mixture Models of Color and Texture Features for Image Classification and Segmentation[J]．Pattern Recgnition，2006，39(4)：695-706．

[20]KAIN A，MACON M，Spectral Voice Conversion for Text-to-speech Synthesis[C]∥Proceeding of the IEEE International Corference on Acoustics，Speech and Signal Processing．Seattle，USA：IEEE，1998：285-288．