对称耦合双振子的复杂运动

张建国，张玉芬

（1.宁夏师范学院教育技术中心，宁夏固原 756000；2.河北大学数学与计算机学院，河北保定 071002）

对称耦合双振子的复杂运动

张建国1，张玉芬2

（1.宁夏师范学院教育技术中心，宁夏固原 756000；2.河北大学数学与计算机学院，河北保定 071002）

建立了一个双弹簧对称耦合的振子系统.计算了通过升维降阶技术得到的一个等价系统的Lyapunov指数，表明振子的运动或为混沌或为准周期.振子中没有引入能量耗散，其运动轨迹因初始条件不同而有很大不同.最后指出，判断这样的系统性态，唯一可靠的方法是计算Lyapunov指数.

耦合振子；Lyapunov指数；运动轨迹；系统性态

弹性振子作为一种极其简单的物理模型，能够展示非常丰富的非线性动力学行为［1－3］，长期以来备受关注.将多个振子耦合在一起，往往能够展示许多物理系统的行为特征，如一个平面上的耦合振子阵列能够模拟表面声波在金属材料中的传播［4－5］，多振子耦合模型能够模拟非刚性分子的振动［6］等等.由于耦合振子具有各式各样的物理背景，对相关模型基本特征进行研究不仅是必要的，而且对理解相关物理系统的特性及其机制是至关重要的.本文建立一个对称双振子模型，通过拉格朗日函数获得其运动方程，数值求解方程获得振子的运动轨迹.结果表明振子的运动强烈依赖于初值，表现在振子运动轨迹因初值不同而不同，且在相空间中做遍历运动.这是因为所考察的振子系统无耗散因素存在，因而是保守系统中典型的非线性动力学行为.Lyapunov指数（exponent）表明所关注的参数组合下系统的运动或为混沌运动或为准周期运动.

必须指出，此前的研究者多不关注耦合振子的运动性态，其研究仅停留在对振子轨迹的描述上.得到的这个结果将提醒相关研究者，当不存在耗散因素时耦合振子系统是一个保守的非线性动力学系统，这样的系统有其固有的动力学特征.另外，一些看似周期的运动实际可能是遍历运动，而遍历运动往往是混沌或准周期的.这种运动单凭肉眼观察振动曲线是无法与周期运动相区别的.

1 对称耦合双振子模型

对称双弹性振子物理模型可以用一个在光滑水平面上运动的质量为m的质点来描述，它与2个弹性系数均为k，原长均为a的弹簧相连.这里，光滑意味着忽略能量耗散，是一个理想体系.平衡时这2个弹簧成一条直线，此时弹簧原长为a，质点在水平的xoy平面内作微小振动.为简单起见，质点平衡位置取在原点o处.模型由图1表示.

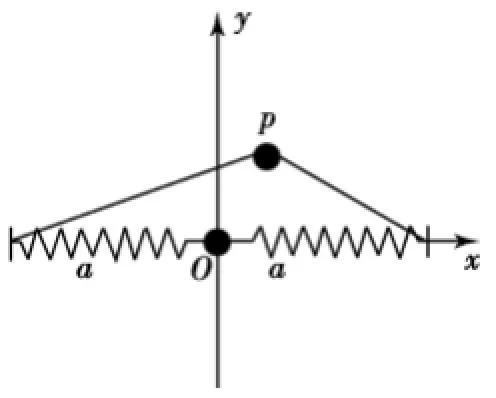
图1 双弹性振子模型Fig.1 Double esastic oscillator model

以下将解析获得系统的运动方程.容易给出此系统的动能和势能，分别是

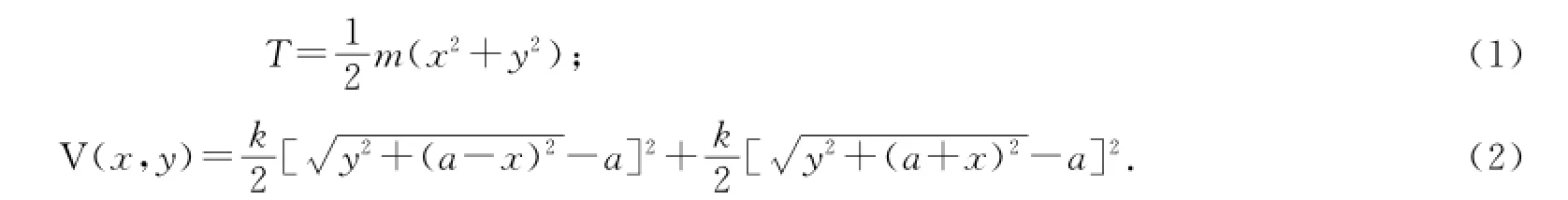
系统的拉格朗日函数可写为

显然，方程（10）和（11）是一组非线性耦合方程.表明线性弹性振子通过相互耦合将转变为非线性振动，体现了简单单元耦合导致新特征涌现的普遍机制.众所周知，这样的非线性方程组很难直接解析求解，将借助于软件Mathematica数值求解.

2 李雅普诺夫指数谱

为了便于计算Lyapunov指数以确定耦合振子运动性态，将通过升维降阶的办法将方程组（10）和（11）化为一阶方程组

这里弹性振子质量m＝1 kg，弹簧原长a＝1.0 m，设弹性系数为控制参量.图2给出系统的Lyapunov指数（Exponent）谱.谱线显示k＜0.074参数范围，绝大多数参数区至少有1个指数大于0，表明振子的运动是混沌的，而在k＞0.074参数范围4个指数值在0附近振荡，表明振子的运动是准周期的或在个别小区域是周期的.

图2 耦合振子模型的Lyapunov指数谱Fig.2 Lyapunov exponent spectrum of the couplled oscillator mode

3 混沌运动

作为一个例子，挑选混沌区的一个参数k＝0.07，取初始条件为x0＝0.25 m，y0＝0.88 m，x·0＝0.009 m／s，y·0＝0.1 m／s，将对应振子的轨迹显示于图3.显然，振子在一个区域之中做遍历运动.由于模型没有考虑能量耗散，因此是一个典型的保守系统.没有耗散性的系统就没有吸引性，因此振子的轨迹均因初态不同而不同，可以说“是一点一线”，意思是一个初态对应一条绝不同于另一初态下的轨迹.明确了混沌和准周期参数区之后，有必要将模型还原为方程组（10），（11）.当然，非常容易理解，方程组（12）－（15）的解在yx平面的投影确信无疑就是原方程组的解.

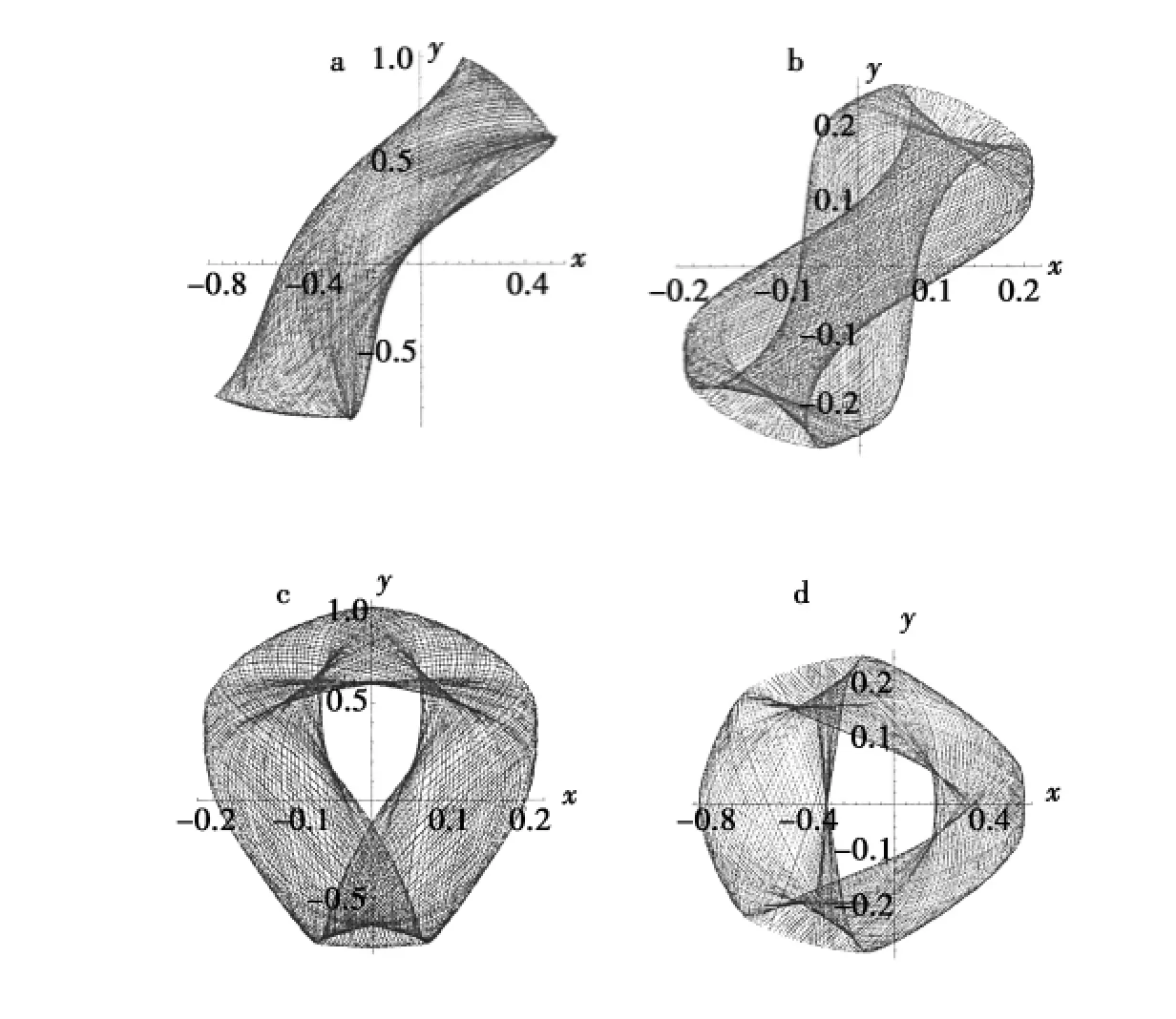
图3 方程组（12）—（15）的解Fig.3 Solutions of equations（12）—（15）

为了使读者获得保守振子“一点一线”的直观映像，获得对这类没有瞬态的动力学的理解，图4给出k＝0.07时3组不同初态下的运动轨迹.其中图a为x0＝0.25 m，y0＝0.88 m，x·0＝0.009 m／s，y·0＝0.1 m／s；图b为x0＝0.4 m，y0＝0.25 m，x·0＝0.001 m／s，y·0＝0.09 m／s；图c为x0＝0.4 m，y0＝0.25 m，x·0＝0.001 m／s，y·0＝0.001 m／s.结果显示了运动轨迹对初始条件的强烈依赖.

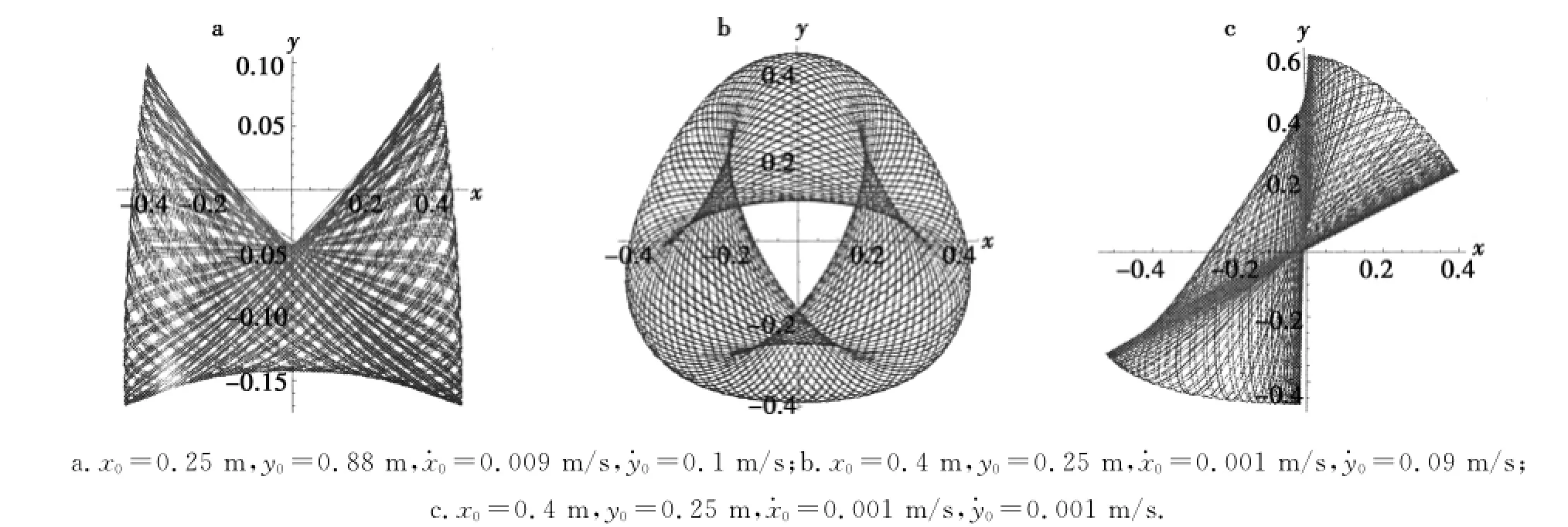
图4 不同初态下振子的混沌轨迹Fig.4 Chaotic trajectories in different initial conditions

4 准周期运动

非线性保守系统“一点一线”的运动特征对准周期运动也不例外.图5给出准周期参数中k＝0.1时3组不同初始条件下振子的准周期运动轨迹，其中图a为

结果表明，振子的准周期混沌运动一样是遍历运动，而且运动轨迹与初态一一对应.但是，单从振子的运动轨迹看，无法区分混沌运动与准周期运动.唯一可靠的办法是计算系统的Lyapunov指数.另外一个必须注意的问题是此前一些单从振动图线做出粗略判断，认为系统做周期运动的作法不妥，往往导致错误认识，因为耦合振子是强非线性系统，混沌的和准周期的遍历运动远比封闭轨道的周期运动普遍.在不引入耗散的情况下，“一点一线”的保守系统特性，使系统运动的复杂性增加了，同时也增加了认识系统性态的难度.

图5 不同初态下振子的准周期轨迹Fig.5 Quai－periodic trajectories in different initial conditions

5 结束语

模拟研究了对称耦合双振子系统的平面运动，由Lyapunov指数判断这个系统既有混沌运动又有准周期运动，当然不排斥一些参数区存在周期运动.由于所考察的系统是一个典型的保守非线性系统，所以即使准周期运动，其运动轨迹强烈依赖于初始条件.周期运动情形与此类似.因此，这样的系统能够展示非常丰富且复杂的运动形态.但必须指出，不借助于Lyapunov指数而单凭对运动轨迹或振动图线的直接观察对系统性态做出判断的作法不妥，往往导致错误认识.

［1］杨正波，夏清华，刘思平.多弹簧振子耦合系统研究［J］.大学物理，2010，29（4）：29－32.

YANG Zhengbo，XIA Qinghua，LIU Siping.Investigation on the motion in coupled system of spring oscillators［J］.Coolege Physics，2010，29（4）：29－32.

［2］商泽进，王忠民.形状记忆合金弹簧振子强迫振动的分贫与混沌［J］.中国机械工程，2010，21（16）：1986－1991.

SHANG Zejin，WANG Zhongmin.Bifurcation and chaos of forced vibration for a shape memory alloy spring oscillator［J］.China Mechanical Engineering，2010，21（16）：1986－1991.

［3］王立明.对称双弹簧振子系统的横振动的主共振与分岔［J］.齐齐哈尔大学学报：自然科学版，2010，26（1）：85－87.

WANG Liming.Primary resonance and bifurcation of the forced transverse oscillation in the symmetric two－springed oscillator［J］.Journal of Qiqihar University：Natural Science Edition，2010，26（1）：85－87.

［4］陈陶，原森，陆建，等.应用弹性振子模型模拟声表现波在金属材料中的传播过程［J］.南京邮电学院学报，2005，25（5）：75－78.

CHEN Tao，YUAN Sen，LU Jian，et al.Numerical simulation of the surface acoustic wave propagaed on the plate surface by mass spring lattice mode［J］.Journal of Nanjing Institute of Posts and Telecommunications，2005，25（5）：75－78.

［5］HERBERT G.Classical mechanics［M］.2nd.Massachusetts：Addison Wesley Publishing Company，1980.

［6］刘裕琴，管立.关于耦合振子运动的研究［J］.工科物理，1999，9（3）：6－8.

LIU Yuqin，GUAN Li.A study of the motion of coupled vibrator system［J］.Engineering Physics，1999，9（3）：6－8.

Complex movement in 2－space of a doubly asymmetric coupled spring

ZHANG Jian－guo1，ZHANG Yu－fen2
（1.Education Technology Center，Ningxia Teachers University，Guyuan 756000，China；2.College of Mathematics and Computer Science，Hebei University，Baoding 071002，China）

A system formed by two springs coupled asymmetrically is suggested.The Lyapunov exponent is calculated in anquivalent system obtained by an increasing dimension and reducing order method.It indicates that the system is chaotic or quasi－periodic in the majority region of the controlled parameter，the elastic coefficient.The trajectories of system bear typical characteristics of a conservative system，that is，one trajectory corresponds uniquely to one set of initial conditions.It should be pointed out that the nature of such coupled oscillators can be revealed only by lyapunov exponent.

coupled oscillator；Lyapunov exponent；trajectory；nature of sy stem

O344

A

1000－1565（2012）02－0144－05

2011－09－12

河北省软科学研究项目（IF2008000236）

张建国（1968－），男，宁夏固原人，宁夏师范学院副教授，主要从事教育技术与非线性科学动力学研究.E－mail：jiaoyujish＠163.com

王兰英）