Banach空间中相对非扩张映射的强收敛定理

刘英，陈永利

（1.河北大学数学与计算机学院，河北保定 071002；2.华北电力大学科技学院，河北保定 071051）

Banach空间中相对非扩张映射的强收敛定理

刘英1，陈永利2

（1.河北大学数学与计算机学院，河北保定 071002；2.华北电力大学科技学院，河北保定 071051）

用修正后的Halpern's迭代方法在Banach空间建立了一个迭代序列，证明了这一迭代序列强收敛到2个相对非扩张映射的公共不动点.

相对非扩张映射；广义投影；Halpern's迭代；正规对偶映射

MSC 2010：47H05

设E是一个Banach空间，E＊是E的对偶空间.〈x，f〉表示f∈E＊在x∈E点的函数值.函数φ：E×E→R定义为

其中J表示E到E＊的正规对偶映射.设C是E的一个闭、凸子集，T是从C到自身的一个映射.用F（T）表示T的不动点集.如果｛x n｝⊂C使得｛x n｝弱收敛到p，而且，则称点p∈C是T的渐进不动点［1］.T的渐进不动点的集合表示为＾F（T）.一映射T：C→C，如果满足：对所有的x，y∈C，‖Tx－Ty‖≤‖x－y‖，则称T为非扩张的，关于非扩张映射的一些研究可参见文献［2］.如果满足：对所有x∈C和p∈F（T），＾F（T）＝F（T）且φ（p，Tx）≤φ（p，x），则称T为相对非扩张的［1］.相对非扩张映射的一些渐近性质可

参见文献［1，3－5］.Halpern［5］建立了如下的迭代序列：

这一迭代序列常常用来逼近非扩张映射T：C→C的不动点.

当空间E有一些较好性质时，迭代序列（1）有下面的一些收敛特点.

1 预备知识

定义正规对偶映射J：E→2E＊为

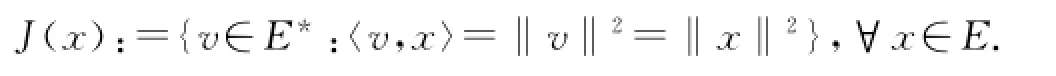
正规对偶映射J有下面的性质：

如果E是自反、严格凸、光滑的Banach空间，那么J是1－1映射，这时J－1是从E＊到E的正规对偶映射，而且也是1－1映射.如果E是一致光滑的，那么J在E的每个有界子集上是一致连续的.

用x n→x和x n⇀x分别表示｛x n｝强收敛到x，和｛x n｝弱收敛到x.

E是一致光滑的当且仅当是连续、单增的函数，而且（0）＝0.E的凸性模δ：（0，2］→ρEE［0，1］定义为

δE（ε）是连续单增函数而且δE（0）＝0.E是一致凸的，那么E有K－K性质.设E是光滑的Banach空间，函数φ：E×E→R定义为

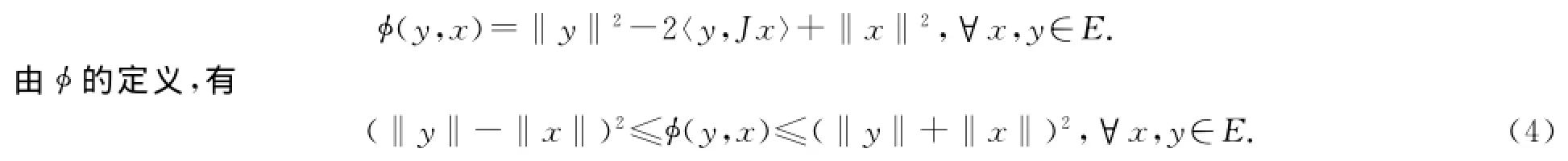
注1［1］如果E是严格凸、光滑的Banach空间，那么对任意的x，y∈E，φ（y，x）＝0当且仅当x＝y.

引理1［1］设E是一致凸和光滑的Banach空间，设｛y n｝，｛zn｝是E中的2个序列，如果φ（y n，zn）→0，而且，｛y n｝或｛zn｝是有界的，那么y n－z n→0.

设C是E的一非空、闭、凸子集，假定E是自反、严格凸、光滑的Banach空间，那么，对任意的x∈E，存在一点x0∈C使得

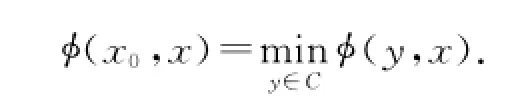
映射ΠC：E→C定义为ΠCx＝x0被称为广义投影［1，8，13］.

引理2［9，14］设C是光滑Banach空间E的一非空、闭、凸子集，设x∈E，那么x0＝ΠCx当且仅当

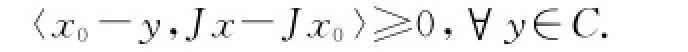
引理3［9，14］设E是自反、严格凸、光滑的Banach空间，C是E的一非空、闭、凸子集，设x∈E，那么

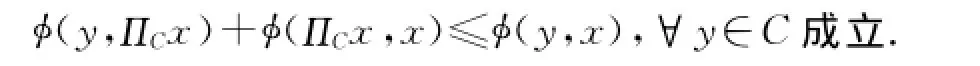
引理4［1］设E是一严格凸、光滑的Banach空间，C是E的一非空、闭、凸子集，设T：C→C是一相对非扩张映射，那么F（T）是闭、凸的.

引理5［15］设E是一致凸的Banach空间，设r＞0，那么存在一连续、严格增的凸函数g：［0，2r］→R使得g（0）＝0和

‖tx＋（1－t）y‖2≤t‖x‖2＋（1－t）‖y‖2－t（1－t）g（‖x－y‖），∀x，y∈Br和t∈［0，1］，

其中Br＝｛z∈E：‖z‖≤r｝.

引理6［16］设E是一个一致凸、一致光滑的Banach空间，如果‖x‖≤R，且‖y‖≤R，那么下面的不等式成立：2L－1R2δE（‖x－y‖／4R）≤φ（x，y）≤4LR2ρE（4‖x－y‖／R），其中L是一常数.

2 主要结果

对任意的x0∈C，定义如下的迭代序列｛x n｝：

定理1 设E是一致凸和一致光滑的Banach空间，C是E的一非空、闭、凸子集，假定T，S是2个从C到自身的相对非扩张映射以致于F＝F（T）∩F（S）≠Ø，那么由式（5）定义的迭代序列｛x n｝强收敛到ΠFx0.

证明 首先表明对每一个n∈N，Cn和Q n是闭凸的.由Cn和Qn的定义，Cn是闭的，Qn是闭凸的；又因

［1］MATSUSHITA S，TAKAHASHI W.A strong convergence theorem for relatively nonexpansive mappings in a Banach space［J］.J Approx Theory，2005，134：257－266.

［2］张丽娟，陈俊敏.有关非扩张映射的带误差的迭代收敛定理［J］.河北大学学报：自然科学版，2007，27（3）：238－240.

ZHANG Lijuan，CHEN Junmin.Weak and strong convergence of a scheme with errors for three nonexpansive mappings［J］.Journal of Hebei University：Natural Science Edition，2007，27（3）：238－240.

［3］BUTNARIU D，REICH S，ZASLAVSKI A J.Asymptotic behavior of relatively nonexpansive operators in Banach spaces［J］.J Appl Anal，2001，7：151－174.

［4］BUTNARIU D，REICH S，ZASLAVSKI A J.Weak convergence of orbits of nonlinear operators in reflexive Banach spaces［J］.Numer Funct Anal Optim，2003，24：489－508.

［5］CENSOR Y，REICH S.Iterations of paracontractions and firmly nonexpansive operators with applications to feasibility and optimization［J］.Optimization，1996，37：323－339.

［6］H ALPERN B.Fixed points of nonexpanding maps［J］.Bull Amer Math Soc，1967，73：957－961.

［7］ISHIKAWA S.Fixed points by a new iteration method［J］.Proc Amer Math Soc，1974，44：147－150.

［8］WITTMANN R.Approximation of fixed points of nonexpansive mappings［J］.Arch Math.1992，58：486－491.

［9］ALBER Y I，REICH S.An iterative method for solving a class of nonlinear operator equations in Banach spaces［J］.Panamer Math J，1994，4：39－54.

［10］SHIOJI N，TAKAHASHI W.Strong convergence of approximated sequences for nonexpansive mappings in Banach spaces［J］.Proc Amer Math Soc，1997，125：3641－3645.

［11］XU Hongkun.Iterative algorithms for nonlinear operators［J］.J London Math Soc，2002，66：240－256.

［12］MARTINEZ C Y，XU Hongkun.Strong convergence of the CQ method for fixed point iteration processes［J］.Nonl Anal，2006，64：2400－2411.

［13］QIN Xiaolong，SU Yongfu.Strong convergence theorems for relatively nonexpansive mappings in a Banach space［J］.Nonl Anal，2007，67：1958－1965.

［14］KAMIMURA S，TAKAHASHI W.Strong convergence of a proximal－type algorithm in a Banach space［J］.SIAM J Optim，2002，13：938－945.

［15］XU Hongkun.Inequalities in Banach spaces with applications［J］.Nonl Anal，1991，16：1127－1138.

［16］CHIDUME C E，KHUMALO M，ZEGEYEH.Generalized projection and qpproximation of fixed points of nonself maps［J］.J Approx Theory，2003，120：242－252.

Strong convergence theorems for two relatively nonexpansive mappings in a Banach space

LIU Ying1，CHEN Yong－li2
（1.College of Mathematics and Computer Science，Hebei University，Baoding 071002，China；2.College of Technology，North China Electric Power University，Baoding 071051，China）

An iteration sequence is proposed in Banach spaces by using the modified Halpern's iteration method.That the iteration sequence converges strongly a common fixed point of two relatively nonexpansive mapping is proved.

relatively nonexpansive mapping；generalized projection；Halpern's iteration；normalized duality mapping

O177.91

A

1000－1565（2012）02－0118－06

2011－04－27

河北省高等学校自然科学研究青年基金资助项目（2010110）；河北省自然科学青年基金资助项目（A2011201053；A2010000191）；国家自然科学基金资助项目（11101115）

刘英（1977－），女，河北邢台人，河北大学副教授，主要从事非线性泛函分析方面的研究.

E－mail：ly＿cyh2007＠yahoo.com.cn

王兰英）