一种全局优化的两阶段算法

张玉芬，王永军

（1.河北大学数学与计算机学院，河北保定 071002；

2.东方地球物理公司研究院数据处理中心，河北涿州 072751）

一种全局优化的两阶段算法

张玉芬1，王永军2

（1.河北大学数学与计算机学院，河北保定 071002；

2.东方地球物理公司研究院数据处理中心，河北涿州 072751）

为了提高算法的有效性，利用梯度算法和粒子群算法独立的运行机制，采用驱赶技术和重新初始化部分群体的技术，提出了一种基于梯度下降法和粒子群算法的两阶段优化算法，并对新算法进行了理论分析和数值仿真.数值结果显示新算法比单纯梯度算法有更好的全局优化能力，比单纯粒子群算法有更快的收敛速度和更高的精度.新算法求解质量更高，运行更稳定.

全局优化；两阶段算法；梯度算法；粒子群算法

全局优化问题广泛应用于金融模型、网络交通、图像处理、集成电路设计、分子生物学、数据库、物流配送系统设计中.因为这些优化问题存在多个不同于全局最优解的局部最优解，所以传统的非线性规划中的局部优化方法不能有效地处理这类问题.而且，随着科学的发展，工程中遇到的优化问题的规模越来越大、复杂性越来越高，这使得全局优化问题的求解变得更加困难.全局优化问题的难以解决阻滞了许多学科的发展，因而全局优化方法的研究显得尤为重要.

梯度类算法是一种确定性的局部优化方法，它能够快速高效地找到临近初始点的局部最优值.常见的算法有最速下降法、牛顿法、拟牛顿法、共轭梯度方法等.它们已经广泛地应用于许多领域［1－5］.此类算法的主要缺点是对初始点的严重依赖性、目标函数和约束区域的拓扑结构的严格要求性.

粒子群算法是一种群体智能优化方法［1］，在粒子群算法中，群体中的一个粒子根据它本身找到的最优位置以及整个群体当前为止找到的最优位置，来不断地调整它本身的位置.算法的核心思想是用当前最好的已知的位置来引导群体朝搜索空间的最优位置移动.粒子群算法设计简单，参数少，容易实现，且表现出了较好的局部跳跃性，已经被应用到许多领域.但算法有时搜索到的只是局部解，找到高精度的解需要较长的运行时间，解决大规模优化问题至今还没有涉及.

文献［2］提出了一种把梯度信息混合到粒子的速度更新公式中加快算法收敛的方法.这种方法没有使用现存的梯度算法的有效性和群体搜索中找到的最优信息.过于强调启发，而改变了传统粒子群算法的核心思想.文献［6］提出了一种基于梯度方法和动态隧道法的混合技术（用GRDT表示）来解决全局优化问题.在GRDT方法中，梯度用来加快局部搜索，动态方程用来寻找好的初始点.但是，该方法需要多次积分动态方程，对高维函数耗时较多，填充函数法和隧道法中的参数较难调节.

1 两阶段算法

1.1 算法原理

不同于一般意义下的进化算法，即局部搜索限制在进化算法的框架内，本文设计了一种新的混和算法.在新算法中，粒子群按照其独有的进化机制演化，而梯度算法使用目标函数的梯度信息进行独立的搜索.粒子群算法起着全局搜索的作用，而梯度搜索起着局部探测的作用.从而把2种算法混合为一个两阶段方法，发挥出它们各自的优点以解决复杂函数的优化问题是本文的核心思想所在.具体而言，第1步，从可行域中随机产生的一点出发，使用梯度算法得到目标函数的一个局部最优点.其次，以得到的最优点为均值，使用高斯分布函数初始化粒子群.然后，在最大的迭代次数内，运用粒子群算法找到一个更好的点.以找到的点作为初始点，回到第1步，重新开始梯度搜索.

另外，为了利用算法已经得到的最优值信息（所有已经找到的局部最优点）防止群体早熟现象，把一种驱赶群体技巧［7］以及部分初始化群体方法加入到新算法中.驱赶技术利用当前点与已经找到的局部最优点之间的距离，建立起一种屏障，使得新产生的点不要落到已经找到的局部最优点太近的范围内，这可以使粒子向着更有希望的区域飞行，同时避免重复搜索.文献［7］已经证明了此方法可以有效地加快群智能算法的收敛.部分初始化群体方法是在群体搜索不能取得全局进展时，使用均匀分布函数产生的部分群体代替当前群体中同等规模的较差个体的一种做法.

1.2 算法步骤

假设群体规模是NP，n是问题的规模，M是一个随机生成的数值，M∈｛1，2，…，NP｝.本文使用的驱赶技术见算法1，更多的信息可以参考文献［5］.本文使用的部分初始化群体技术执行如下：根据当前群体的适应值进行排序，在可行域中按均匀分布随机产生M个样本点，执行驱赶技术，然后代替当前群体中M个较差的个体，其余NP－M个个体保留在群体中，进而形成同等规模的新群体.新群体继续执行粒子群算法搜索.新算法记做GRPSO（gradient based particle swarm optimization method），见算法2.

算法1 驱赶技术［5］

步骤0.输入算法找到的极小点集S＊＝｛X＊j（j＝1，2，…，m）｝，这里的m是找到的极小点的个数.给定小生境的半径rij与驱赶因子mij.

步骤1.对群体中的每一个粒子Xi，i＝1，2，…，NP.

步骤1a.计算距离d ij＝｜X i－X＊j｜j＝1，2，m.

步骤1b.对集合S＊中的每一个元素X＊j，j＝1，2，…，m.

如果d ij＜rij，那么令Zij＝（X i－X＊j）／d ij.然后置X i＝Xi＋Pij Z ij.

步骤2.输出群体Xi，i＝1，2，…，NP.

算法2 提出的新算法（GRPSO）

步骤0.随机生成可行域中的初始点X0，并置局部搜索计数器k＝0.给定粒子群内部的最大迭代次数Smax和计数器Npso＝1、调用粒子群算法的最大次数SSmax.设最优点集合S＊＝Φ.

步骤1.（局部搜索）从Xk出发，应用梯度下降法找到可行域中的1个极小点X＊k，同时保留到集合S＊中.

步骤2.（使用粒子群算法的全局搜索）

步骤2a.根据高斯分布，以X＊k为均值，在可行域中初始化群体，并找出最好个体gbest.若f（X＊k）＜f（gbest），令gbest＝X＊k，k＝1转步骤1.否则，令gbest＝X＊k，计数器SS＝1，转入步骤2b.

步骤2b.当最大迭代次数Smax没有达到时

1）更新pbest，如果当前个体适应值好于f（pbest），i＝1，2，…，NP.

2）更新gbest，如果当前群体中的最优个体适应值好于f（gbest）.

3）如果f（gbest）＜f（X＊k），令X＊k＝gbest，结束循环.

4）根据速度更新公式（1）和位置更新公式（2）更新群体的速度和位置.

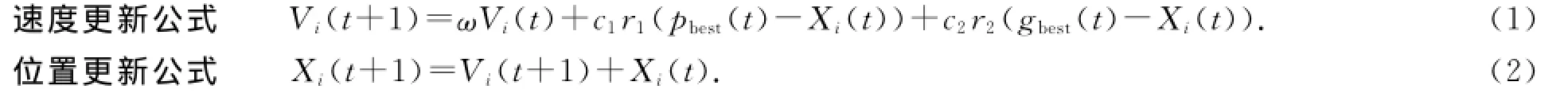
5）把当前群体和极小点集S＊作为输入集，执行算法1的驱赶技术（Algorithm 1）.然后，令Npso＝Npso＋1.

步骤2c.如果gbest＝X＊k，SS＝SS＋1.

如果SS＞SSmax，停止计算并输出gbest＝X＊k.否则，重新初始化M∈｛1，2，…，NP｝个粒子，并执行算法1的驱赶技术，保证此M个粒子远离找到的局部最优点.令Npso＝＋1，转入步骤2b.否则，令X＊k＋1＝gbest，k＝k＋1，转入步骤1.

2 实验结果与分析

2.1 实验结果

用文献［3］中已经被GRDT测试过的10个函数来检验新算法的优化性能.首先，把函数值的计算次数设定为2 100，比较最终解的质量，数值结果见表1.用新算法GRPSO对10个标准测试函数进行优化，把运算的结果与其他的算法，如GRDT（梯度算法和动态隧道法的混合方法［3］）、HGPSO（混合粒子群算法［6］）和专门设计处理高维函数的GRADSA（混合梯度和模拟退火技术的算法［4］）做比较.由于解的质量、收敛速度（计算机的CPU时间或目标函数值的计算次数）、算法的寻优成功率是衡量算法优劣的主要标准，对10个复杂函数［3］的20次独立运行后这几个指标的平均结果总结如表1.然后，在给定的最大函数值计算次数下，比较算法找到给定精度的解的成功率，数值结果见表2和3.

表1 新算法、GRDT以及其他的文献找到的函数最优值Tab.1 Optimal value of functions by the new algorithm，GRDT method and other algorithms in bibliography

表2 新算法和其他文献提到算法的函数值平均计算次数Tab.2 Average numbers of functions by the new algorithm and other algorithms in bibliographies

表3 新算法和HGPSO方法的成功率Tab.3 Rate of success in computation by the new algorithm and HGPSO method

2.2 结果分析

从表1可以看出，GRPSO可以找到所有测试函数的最优值，其结果接近理论上的分析值.与GRDT和其他文献报道的结果相比，新算法找到的结果更好一些，比如函数H3和SH是2个典型的例子.

从表2和3可以看到，新算法HGPSO运行效果更好，尽管它们都是基于梯度搜索的混PSO算法.同时，数值结果意味着在同样给定的计算时间内，新算法可以得到比GRPSO更高精度的解.说明两阶段的独立搜索更有助于各个算法发挥其基本功能.

从表2可以看出，根据函数值的计算次数，新算法优化性能高于GRDT和HGPSO方法，尤其对于GP和H3函数的优化效果更明显.与其他典型方法如PRS（纯随机搜索）、MS（多起点方法）、SA1（基于微分方程的模拟退火方法）、SA2（基本模拟退火方法）、TS（禁忌搜索）、TA（树退火）和TT（信赖方法TRUST）相比，新算法的计算量大大降低.

总之，梯度算法帮助新算法加快局部收敛，并找到高精度的解.加入了驱赶技术和部分初始化群体的粒子群算法增加了群体多样性，防止了群体早熟，进而使新算法能有效地跳出局部最优.所有这些显示新算法对低维的复杂函数优化效果好.

3 结论

提出了一种基于梯度算法和粒子群算法的两阶段混和算法.从有效的局部搜索（使用梯度算法）开始，然后借助进化算法（采用粒子群算法）的全局跳跃性质探索更有希望区域，为局部搜索找到更好的出发点.寻找高精度的解由局部搜索完成，因而省却了演化算法的进化时间，粒子群算法的全局搜索信息得以利用.不同于一般框架下的演化算法，该算法有效地利用了梯度算法和粒子群算法独立的运行机制.另外，新算法中采用了驱赶技术和重新初始化部分群体的技术.数值结果显示新算法比单纯梯度算法有更好的全局优化能力，比单纯粒子群算法有更快的收敛速度、解的精度.

［1］KENNEDY J，EBERHART R C.Particle swarm optimization［Z］.Proceedings of IEEE International Conference on Neural Networks，Perth Australia，1995.

［2］ROY C P，SINGH Y P，CHANSARKAR R A.Hybridization of gradient descent algorithms with dynamic tunneling methods for global optimization［J］.IEEE T Syst Man Cy，2000，30（3）：384－390.

［3］NOEL M M，JANNETT T C.Simulation of a new hybrid particle swarm optimization algorithm［J］.System Symposium，2004，32（4）：150－153.

［4］SUGANTHAN P N.Particle swarm optimiser with neighbourhood operator［Z］.Proceedings of the IEEE Congress on Evolutionary Computation，Piscataway，NJ，1999.

［5］PARSOPOULOS K E，VRAHATIS M N.On the computation of all global optimizers through particles warm optimization［J］.IEEE Trans on Evolutionary Computation，2004，8（3）：211－224.

［6］刘星宝，蔡自兴，王勇.用于全局优化问题的混合免疫进化算法［J］.西安电子科技大学学报，2010，37（5）：971－980.

LIU Xingbao，CAI Zixing，WANG Yong.Hybrid immune evolutionary algorithm for global optimization problems［J］.Journal of Xidian University，2010，37（5）：971－980.

［7］路克中，王汝传，章家顺.最优化问题全局寻优的PSO－BFGS混合算法［J］.计算机应用研究，2007，24（5）：17－19.

LU Kezhong，WANG Ruchuan，ZHANG Jiashun.PSO－BFGS algorithm of global optimum for optimization problems［J］.Application Research of Computers，2007，24（5）：17－19.

A two－phase algorithm for global optimization

ZHANG Yu－fen1，WANG Yong－jun2
（1.College of Mathematics and Computer Science，Hebei University，Baoding 071002，China；2.Date Processing Center，Geophysical Prospecting Research Institute，Zhuozhou 072751，China）

To enhance effectiveness of algorithm，on the basis of analyzing the independent operating mechanism of both gradient algorithm and particle swarm algorithm，a two－phase optimization algorithm based on gradient descent and particle swarm algorithm is presented；it adopts the driving technique and the re－initialization technique of part of population.Then，the theoretical analysis and numerical simulation about the new algorithm are made.The numerical simulation shows this new algorithm has better global optimization ability than the gradient algorithm，and it has faster convergences speed and lighter solution accuracy than particle swarm algorithm.This new algorithm produces a lighter quality solution and has more stable operation.

global optimization；two－phase algorithm；gradient algorithm；particle swarm op timization

O241.3

A

1000－1565（2012）02－0207－05

2011－09－11

河北省软科学研究计划项目（11457250）；河北省自然科学基金资助项目（F2009000236）

张玉芬（1964－），女，河北肃宁人，河北大学副教授，主要从事不确定信息处理方向研究.E－mail：happy6002＿cn＠sina.com

孟素兰）