对数平均温差中试差法计算
刘义章
对数平均温差中试差法计算
刘义章
传热操作型计算中,常遇到对数平均温差的试差计算以确定流体的某一个温度。教材中没有讲解如何计算,学生普遍反映不知从哪儿开始进行试差。该研究从试差法的计算步骤和试差范围的确定方法来讲解计算技巧,以便学生掌握和供同行参考。
传热;试差法;对数平均温差
在工程计算中,经常会遇见一个方程解一个未知数无法通过常规方法求解的情况,这是学生在中学学习中没有经历过的。在化工原理课程的学习中,需要用试差计算解决一些工程计算问题,如管子规格的选择、对数平均温差的温度计算等。现就对数平均温差中试差法计算分析,了解试差法计算技巧,帮助学生提高工程计算能力。
传热操作型计算用于判断一个现有的换热器能否完成指定的生产任务,或预测某些参数的变化对换热能力的影响。这种计算的一个共同特点是要用到试差计算。现就教材中的例题分析如下:(陆美娟主编的《化工原理》,高职高专教材上册163页)
某厂用初始温度为25℃的冷却水将流量为1.4Kg/s的气体从50℃逆流冷却到35℃,换热器面积为20m2总传热系数为230W/(m2·℃)。已知气体平均比热容为1.0KJ/(Kg.℃)。试求冷却水的用量及出口温度。
教材中的解法是:
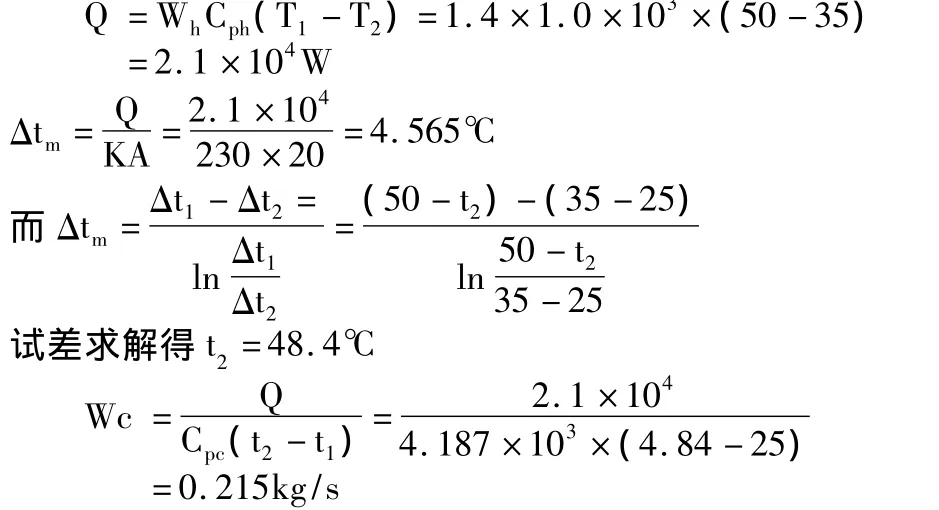
此题的关键计算在于由△tm试差计算出t2。教材中忽略了试差过程,其他教材也没有具体讲解。学生反映出的问题是从什么温度开始试差,有什么样的解题技巧,可以又快又准计算。书中虽然提到一点,但并不能满足实际计算的要求。究竟如何试差,可从以下几个方面入手。
一 判断能否用算术平均值法试差
当△t2最大值等于△t1,此时△tm=△t2-△t1,当△t2最小值等于△t1,此时△tm=△t1;即若△t1>△tm>△t1时,就可用算术平均值法试差。此时由△tm=确定△t2值,再算出t2进行试差;若不能满足△t1>△tm>△t1,就不能用算术平均值法试差,得改用下一步方法判断。在此题中因为×10℃ =7.5℃ >4.56℃,所以不能用算术平均值法试差。
二 由△t2、△t1和△tm的关系判断试差的温度范围
教材中习惯把温度差较大的用△t1表示,温度差小的用△t2表示,由对数平均温差的概念可知△t1>△tm>△t2,在此题中,T2-t1=35 -25=10℃ > △tm=4.565℃,所以,T2-t1=△t1=10℃,因此△t2=T1-t2<△tm,而且有 t2>T1-△tm=50 -4.565=45.435℃,又因为 t2总小于T1,即t2<50℃,这样,试差温度范围被缩小到(45.435,50)之间。用中间截断法试差,如:设t2=48℃代入
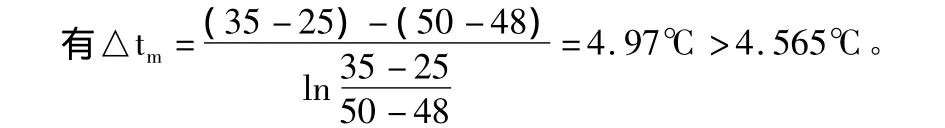
三 根据第一次试差结果的大小关系判断试差值t2的大小关系
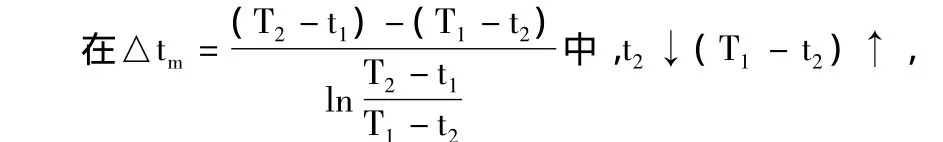
由第2步和第3步方法试差可不必考虑算术平均值法试差,此方法具有普遍性。教材中的叙述很容易误导学生解题,存在不足之处。对于能利用算术平均值法试差的类型举例如下:
已知T1=80℃ T2=60℃ t1=20℃ t2=40℃若由原来的并流换热改为逆流换热,其它工艺条件不变,求t'2
解:并流时

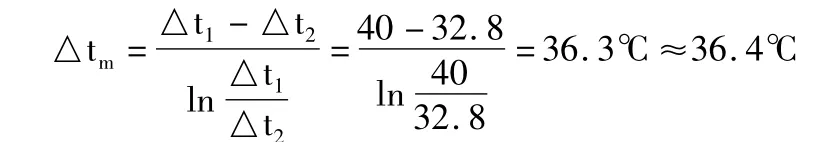
由于 36.3 与 36.4 很接近,可结束解题,即 t'2=47.2℃
若数值要求精确可再设t'2=47℃代入
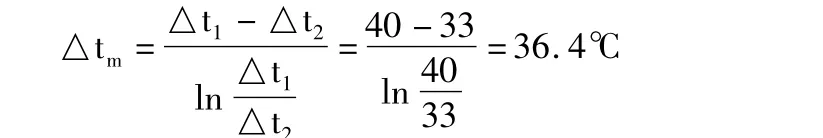
解题结束。
综上所述:如果△tm可以用算术平均值法计算,就无须试差,即使试差也比较快;但实际应用常常不能用算术平均值法计算。有了以上的论述,在解题中就能得心应手,掌握解题技巧,提高解题速度。
LMTD in the Trial and Error Method
Liu Yizhang
Operational heat transfer calculations are often encountered in the logarithmic mean temperature difference(LMTD)of trial and error calculations to determine the fluid in a certain temperature.Textbooks do not explain how to calculate,the students generally do not know how to reflect the trial and error.This article explains the calculation techniques for students from the calculation steps and the scope of trial and error method.
heat transfer;trial and error method;LMTD
TK124
A
1672-6758(2012)05-0137-2
刘义章,硕士,讲师,滁州职业技术学院基础部,安徽·滁州。研究方向:多相催化、教学。邮政编码:239001
安徽省省级示范实验实训中心建设项目(项目号:20101427);滁州职业技术学院《化工原理》院级精品课程项目(项目号:YJ2010009);应用化工技术特色专业(中央财政支持高等职业学校提升专业服务能力项目)(项目号:2011123)
Class No.:TK124Document Mark:A
(责任编辑:郑英玲)

