基于小波变换的大尺度岩体结构微震监测信号去噪方法研究＊

徐宏斌 李庶林， 陈际经

1）中国福建厦门361005厦门大学建筑与土木工程学院

2）中国湖南郴州423037湖南柿竹园有色金属有限责任公司

基于小波变换的大尺度岩体结构微震监测信号去噪方法研究＊

徐宏斌1）李庶林1），陈际经2）

1）中国福建厦门361005厦门大学建筑与土木工程学院

2）中国湖南郴州423037湖南柿竹园有色金属有限责任公司

为将小波去噪方法应用于大尺度岩体结构微震监测信号的去噪研究，首先在MATLAB环境下进行仿真，验证了使用Symlet6小波进行小波去噪的可行性；利用4种自适应阈值规则对含噪信号进行去噪对比，结果表明4种阈值去噪后的信号在均方差较小的情况下都极大地提高了信号的信噪比，有效地去除了噪声，对不同的含噪信号，无偏似然原则阈值去噪后的信噪比最高，同时均方差也最小，在去噪时显得更为有效；以柿竹园全数字多通道微震监测系统为背景，将MATLAB仿真结论应用于现场微震信号的去噪研究，结果表明小波阈值去噪特别适合大尺度岩体微震信号这一类非稳定信号的去噪分析，既可以对低信噪比的微震信号提取出有效信号，也可以对频率覆盖范围广的微震信号在各尺度上提取并重构出有效信号，实现了对微震真实信号和噪声信号的有效分离.

小波去噪 大尺度岩体 微震技术 MATLAB仿真

引言

微震监测技术作为一种先进的实时监测技术，在地下工程安全监测和防灾减灾监测方面具有较好的应用价值和前景（李庶林，2009）.自2003年本文作者在凡口铅锌矿建立起了我国矿山地压监测的第一套全数字型64通道微震监测系统以来（李庶林等，2005），全数字多通道微震监测系统开始在国内得到了较多的应用，尤其是在矿山等大尺度岩体结构的稳定性和地压监测方面，为矿山的安全生产提供了有力的技术支撑.微震监测技术是一门典型的理论落后于实践的技术，该技术在应用领域还有许多亟待解决的应用理论和技术问题.通常，微震系统的工作环境复杂，采集的信号包含着各式各样的噪声，因此对微震监测系统采集到的信号进行去噪和提纯就是其中一个重要问题，它是准确计算信号特征参量以及精确定位微震事件的前提.

传统的信号处理方法包括低通、高通和带通滤波，这些方法对信号的处理是比较粗略的，在噪音环境比较简单的情况下是适用的.但是对于噪声环境复杂的微震信号而言，传统方法就显现出了局限性，既不能有效地去除各频段的噪声，也不能在去除噪声的同时有效地保留信号的细节信息.小波变换在时域和频域都有很好的局部化性质，具有多分辨率分析的特点，在非稳定信号的去噪分析方面具有重要的应用.Mallat和Hwahg（1992）提出的利用小波变换模极大值原理进行信号去噪的方法是小波去噪中最经典的方法.Xu等（1994）提出了一种基于空域相关性的噪声去除方法.Donoho和Johnstone（1994）提出了信号去噪的软阈值方法和硬阈值方法.同年，Coifman和Donoho（1994）提出了平移不变小波去噪.Johnstone和Silverman（1997）给出一种相关噪声去除的小波阈值估计器.Chang等（2000）提出一种针对图像的空域自适应小波阈值去噪方法.Zhang和Salari（2005）提出了基于神经网络的图像去噪算法.近年来，基于小波的去噪方法在国内信号处理和图像处理中得到了较为广泛地研究（潘泉等，2005）.已经开始有部分学者将小波去噪技术应用于岩石类材料的微震、声发射研究中.赵奎等（2006）通过确定室内岩石声发射实验Kaiser点信号的频率范围，提出了基于小波变换的Kaiser点信号的信噪分离方法.王更峰（2006）对室内岩石声发射信号进行小波消噪，并提出了基于能量阈值法的小波包消噪.金解放等（2007）总结了适合于室内岩石声发射信号分析和处理的小波基应具有的特点，并在理论上归纳出Daubechies小波族中的Db4小波基能满足岩石声发射信号处理的要求.许大为等（2008）对小波去噪方法在矿山微震信号的去噪研究中进行了初步的应用研究，指出小波去噪方法可应用于微震信号的预处理.

目前，将小波去噪方法应用于岩石类材料的微震、声发射技术的研究较少，研究范围也多限于室内实验，尤其是基于全数字多通道微震监测系统的现场实际应用研究尚未看到.鉴于此，本文依托柿竹园矿微震监测系统（袁节平等，2010），在仿真实验的基础上，将小波去噪技术应用于现场微震监测信号的去噪研究.

1 小波变换基本理论

1.1 连续小波变换

连续小波变换（continuous wavelet transform，简写为CWT）（潘泉等，2005）定义为

其中函数系

1.2 离散小波变换

对连续小波变换的定义式中，将其尺度参数a和平移参数b进行如下的离散化采样：

则对应的离散小波为

离散小波变换的定义为

1.3 Mallat算法

在应用这些Mallat快速算法做时频分析时，只需要分析信号的有关数据和二尺度方程的传递系数｛h（k）｝和｛g（k）｝，并不涉及尺度函数φ（t）的具体表达式.

分解算法要实现的目标是：在｛φ（t－k）｝是标准正交基条件下，已知｛h（k）｝和｛g（k）｝，求出｛cj，k｝（cj－1，k的近似信号）和｛dj，k｝（cj－1，k的细节信号）.其具体的计算公式为

对于公式（6）和公式（7），可以用更为简单的图形表示.记Aj＝｛cj，k｝，Dj＝｛dj，k｝表示公式（6）和公式（7）所表达的运算，则Mallat分解算法可用图1展示分解算法结构示意图.

信号经过分解处理后，便要进行信号的重构，就要用到重构算法.重构算法作为分解算法的逆过程，其计算公式为

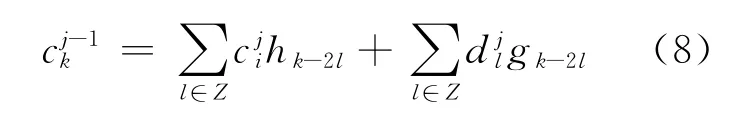
2 小波阈值去噪原理

目前比较常用的去噪方法有3种：模极大值去噪法、空域相关去噪法和小波阈值去噪法.本文的研究选用的是应用最广泛的小波阈值去噪法.

令基本的噪声模型表示为

式中，e（n）为噪声，σ为噪声强度.

小波分解过程如图2所示.一般来说，一维信号的阈值消噪过程可分为以下3个步骤进行：

1）计算含噪信号的正交小波变换.选择一个正交小波并确定一个小波分解的层次N，然后对信号x（n）进行N层小波分解.

2）对小波系数进行非线性阈值处理.为保持信号的整体形状不变，保留所有的低频系数，对第1到第N层的每一层高频系数，采用硬阈值或软阈值方法进行量化处理.

3）进行逆小波变换.根据小波分解的第N层的低频系数和经过量化处理后的第1层到第N层的高频系数，做逆小波变换进行重构，得到恢复的原始信号的估计值.

3 阈值的量化和阈值选取

3.1 阈值的量化规则

硬阈值处理是把信号小波变换系数的绝对值与阈值比较，小于或等于阈值的小波系数变为零，大于阈值的点保持不变.软阈值处理则是把比较后小波系数大于阈值的点变为该点与阈值的差值.用公式表示为

硬阈值

软阈值

3.2 阈值的选择

小波去噪有4种自适应阈值原则可供选择（潘泉等，2005）：无偏似然估计原则、固定阈值原则、启发式阈值原则和极值阈值原则.

1）无偏似然估计（sure）原则.无偏似然估计原则是一种基于stein无偏似然估计（二次方程）原理的自适应阈值选择.对一个给定的阈值t，先得到它的似然估计，再将似然t最小化，就得到了所选的阈值，它是一种软阈值估计器.

2）固定阈值原则.固定阈值计算公式如下：

式中，n为信号x（i）的长度，T为阈值.

3）启发式阈值原则.启发式阈值原则是无偏似然估计原则与固定阈值原则的折中.如果信噪比很小，即按无偏似然估计处理；如果信噪比较大，则采用固定阈值原则处理.

4）极值阈值原则.极值阈值原则采用极大极小原则选择阈值，它产生一个最小均方误差的极值，而不是没有误差.计算公式如下：

4 小波阈值去噪的仿真实验分析

本节进行小波阈值去噪的仿真实验分析，针对小波基的选取以及去噪阈值的不同对去噪效果的影响进行对比分析，寻求可用于微震信号去噪分析的小波及去噪阈值.

为了更加精确以及量化评价去噪效果，定义信噪比（SNR）和均方差（RMSE）两个参数.设原信号为x（n），去噪后的信号为x（n）′，则信噪比的定义为

原始信号和去噪后信号的均方根误差定义为

信噪比越高，均方根误差越小，去噪信号就越接近原始信号，去噪效果就越好.

4.1 小波基的选取

金解放等（2007）指出Db4小波基能满足岩石声发射信号处理的要求.本文选用经典的symlet小波对几种不同类型的含噪信号进行小波去噪，来检验使用symlet小波进行小波去噪的可行性.为了便于比较去噪结果，小波分解采用symlet6小波对信号进行5层分解，采用启发式阈值进行去噪，阈值量化为软阈值.

1）信噪比为5的冲击（bump）信号.含噪冲击信号的原信号及去噪后信号如图3所示.

2）信噪比为5的块状（block）信号.含噪块状信号的原信号及去噪后信号如图4所示.

3）信噪比为5的宽正弦（heavysin）信号.含噪宽正弦信号的原信号及去噪后信号如图5所示.各种信号去噪后的信噪比和均方根如表1所示.

表1 去噪后信号的信噪比和均方根Table 1 SNR and RMSE of denoised signal

从表1可以看出，选用symlet小波去噪可以对不同类型的含噪信号进行有效地去噪，在均方差较小的情况下，极大地提高了信号的信噪比，较好地重现了含噪前的真实信号，可以用于信号的去噪应用.

4.2 不同去噪阈值的去噪结果分析

为了便于比较不同阈值的消噪结果，选用4.1节中的symlet6小波，分解层数为5层，分别以无偏似然估计阈值、固定阈值、启发式阈值和极值阈值对该节中信噪比为5的冲击信号、块状信号以及宽正弦信号进行消噪，阈值量化为软阈值.限于篇幅，只给出冲击信号的原信号及去噪后信号，如图6所示.

含噪冲击信号、块状信号和宽正弦信号4种阈值去噪后信号的信噪比和均方根分别如表2—4所示.

表2 冲击信号去噪后的信噪比和均方根Table 2 SNR and RMSE of denoised bump signal

表3 块状信号去噪后的信噪比和均方根Table 3SNR and RMSE of denoised blocks signal

从表2—4中可以看出4种阈值去噪的均方差都较小，都极大地提高了信号的信噪比，有效地去除了噪声.经比较可以发现，对不同的含噪信号，无偏似然原则阈值降噪后的信噪比最高，同时均方根误差也最小，在去噪时显得更为有效，既能有效地去除了噪声，同时也能保留信号里的高频信息.因此，下文中利用小波阈值去噪对现场微震信号进行去噪时将选用无偏似然原则阈值.

表4 宽正弦信号去噪后的信噪比和均方根Table 4 SNR and RMSE of denoised heavysin signal

5 大尺度岩体结构微震监测信号的小波阈值去噪

5.1 柿竹园矿微震监测系统介绍

柿竹园多金属矿位于湖南省郴州市苏仙区境内，自1987年采用分段凿岩阶段矿房法开采以来，因种种原因井下的采空区（矿房）未能进行处理，截止2002年，井下留下占矿段约60%的矿柱矿量和近300万m3的巨大采空区群，累计顶板暴露面积达3万m2，连续顶板暴露面积近1万m2，15m厚的连续条带矿柱多处垮塌.由于采空区量大集中，暴露时间长，大爆破振动影响频繁和受破碎带与岩体结构面的影响，以及应力集中导致矿柱破损等，残留大尺度矿柱结构稳定性安全问题凸显.

针对常规的地压监测缺点，柿竹园多金属矿于2008年引进国际先进的全数字型多通道微震监测系统，可进行全范围立体空间实时监测.柿竹园矿多通道全数字型微震监测系统为加拿大ESG公司第四代全数字型监测系统，共计5台Paladin数据采集仪（30个通道），携带30个单轴加速度传感器.该系统在组成上由地表数据处理站、井下微震数据采集仪、井下传感器三大部分组成.

5.2 微震监测信号的小波阈值去噪

柿竹园微震系统自建立以来，采集了大量的微震波形信号，现已建成波形数据库，为微震技术及理论的进一步研究提供了宝贵的数据.经过长期的现场研究，已形成系统和有效的微震信号辨识方法，包括经验分析法、理论分析法和综合分析法等.但这只是信号处理的初步，辨识后的各种信号仍然含有各种随机噪声.噪声对信号参数计算以及微震事件定位会产生不同程度的影响，微震信号还需进一步的信号去噪研究.

本部分将选用现场采集到的几种典型的微震信号，利用4.1节仿真实验的结论，采用symlet6小波及无偏似然原则阈值进行去噪研究，阈值量化为软阈值，小波分解层数为5层.需要指出的是，本部分的所有信号都采用传统去噪方法中的带通滤波器进行了初步的去噪，获得包含有效信号频率段50—5 000Hz范围内的信号.当然，初步带通去噪后信号中依然还包含有其它噪声.

1）可定位岩体破裂事件.岩体破裂信号是指岩石或岩体在应力的作用下产生破裂时产生的弹性波信号，是微震监测的主要对象.包括岩体受力变形、产生裂纹、裂纹扩展、产生裂缝、裂缝扩展等过程产生的微震信号，也包括岩体错动、片帮、崩落、冒顶、岩爆、大爆破后的余震、滑坡以及大规模岩体失稳导致的矿震等微震信号.可定位岩体破裂事件是指震源激起弹性波的能量较大，可以被多个传感器感应、接收并产生触发，可由系统定位软件计算出具体位置的事件.

图7a所示的岩体破裂事件信号，是在柿竹园矿一次大爆破后由于矿体应力重分布引起的能量较大的岩体破裂信号；图7b为小波阈值去噪后的波形图；图7c为岩体破裂事件信号的小波分解各尺度波形图，可以看到，各尺度都包含着明显的有效微震信号，如果选用常用的低通或带通滤波器将会遗失大量的有效信息；图7d为各尺度细节小波系数作用阈值的过程，在每个尺度进行阈值去噪，去除噪声，保留有效信号.

岩体破裂及爆破事件信号去噪后的信噪比和均方根如表5所示.

表5 岩石破裂及爆破去噪后信号的信噪比和均方根Table 5 SNR and RMSE of denoised rock mass fracture signal and denoised blast signal

图8给出了可定位岩体破裂信号中的噪声及其频谱图.由图8b可以看到，随机噪声频率分布范围较广，从几十Hz到3 000Hz.如果为了去除噪声，选择3 000—5 000Hz的带通滤波器，则单纯对频域的滤波有“一刀切”的缺陷，对带通之外的频谱不加区分的去除的同时也过滤掉了很多有效信号.

2）爆破信号.爆破信号是系统监测到的主要事件之一.当研究爆破对岩体稳定的影响或爆破波在岩体中的传播衰减较规律时，它是系统研究的对象，爆破信号能量大，一般都为可定为事件.

图9a所示的爆破事件信号，是柿竹园矿某一次爆破的信号波形；图9b为小波阈值去噪后的波形图.限于篇幅，未给出小波分解各尺度波形图以及各尺度细节小波系数作用阈值的过程.

图10给出了爆破信号中的噪声及其频谱图.由图10b可以看到，随机噪声频率分布范围从几十Hz到5000Hz，涵盖了非常广的频率段.通过以上的分析可以发现，对于能量较大的定位事件，降噪后的信号消除了含噪信号中覆盖的较强的随机噪声和毛刺现象，并且与原信号具有同等的光滑性；降噪后信号的信噪比和均方差均达到理想的数值，能有效地区分信号中的突变部分和噪声，实现了在各个尺度上进行去噪，较好地重现了含噪前的真实信号.

3）不可定位岩体破裂事件.不可定位岩体破裂事件在这里指的是单通道岩体破裂事件或者事件只有被2—3个传感器触发的岩体破裂事件，事件能量较可定位事件小.不可定位岩体破裂事件的有效辨识对微震日常监测具有极其重要的意义，它直接反应各个传感器临近区域岩体稳定性和地压活动性的相对程度.并且，由于是能量较小的破裂，得到时域上事件数或相对能量值的演变特征后，结合现场考察情况进行分析总结，并寻求相关理论的合理解释，这对研究和评价岩体失稳过程具有重要的意义.

图11a所示的微震监测系统采集到的一段波形数据，从波形图中可以初步判断该段波形图包含着岩体破裂事件，但由于能量较小，被噪声强烈的干扰，岩体破裂事件的有效波形信号不明显，其起跳和衰减的过程都不清晰；图11b是小波阈值去噪后的信号，可以清楚地看到，该段波形包含3个能量较小的岩体破裂事件，小波阈值去噪实现了在低信噪比情况下有效地提取真实的岩体破裂信号.

通过以上的分析可以看到，小波阈值去噪既可以对低信噪比的微震信号提取有效信号，也可以对频率覆盖范围广的微震信号在各尺度上提取有效信号，实现了对微震信号真实信号与噪声信号的有效分离.小波阈值去噪特别适合于大尺度岩体结构微震信号这一类非稳定信号的去噪分析，是微震信号进行有效提纯和进一步信号分析的有效工具.

6 讨论与结论

大尺度岩体结构的稳定性分析是一个复杂的研究内容，微震监测技术是研究大尺度岩体结构稳定性的一个有力的手段.全数字多通道微震监测系统的建立，实现了对工程现场大尺度岩体结构的实时全过程监测，解决了传统声发射技术现场工程应用数据不完整性的问题.本文采用小波阈值去噪理论实现了微震信号的信噪分离.基于小波的信号分析，如微震信号特征参量的准确计算、微震事件的精确定位等极具研究意义.可以预见的是，如果采用更为先进的小波理论进行微震信号的信号分析，将会有力地推进微震监测技术的发展.

本文得到以下结论：

1）通过Matlab仿真实验，symlet6小波满足小波阈值去噪的要求，验证了使用symlet6小波进行小波去噪的可行性.

2）4种阈值去噪的均方差都较小，都极大地提高了信号的信噪比，有效地去除了噪声.对不同的含噪信号，无偏似然原则阈值降噪后的信噪比最高，同时均方根误差也最小，在去噪时显得更为有效.

3）小波阈值去噪特别适合于大尺度岩体微震信号这一类非稳定信号的去噪分析，既可以对低信噪比的微震信号提取有效信号，也可以对频率覆盖范围广的微震信号在各尺度上提取有效信号，实现了对微震信号真实信号与噪声信号的有效分离.

金解放，赵奎，王晓军，赵康.2007.岩石声发射信号处理小波基选择的研究［J］.矿业研究与开发，27（2）：12－15.

李庶林.2009.试论微震监测技术在地下工程中的应用［J］.地下空间与工程学报，5（1）：122－128.

李庶林，尹贤刚，郑文达，Trifu C.2005.凡口铅锌矿多通道微震监测系统及其应用研究［J］.岩石力学与工程学报，24（12）：2048－2053.

潘泉，张磊，孟晋丽，张洪才.2005.小波滤波方法及应用［M］.北京：清华大学出版社：3－5.

王更峰.2006.基于小波分析的岩石声发射信号处理技术［J］.矿业工程，4（5）：11－14.

许大为，潘一山，李国臻，王岩.2008.基于小波变换的矿山微震信号滤波方法研究［J］.地质灾害与环境保护，19（3）：74－77.

袁节平，胡静云，周爱民，林峰，陈际经，李庶林.2010.柿竹园多通道微震监测系统的建立及其应用［J］.矿业研究与开发，30（6）：12－14.

赵奎，邓飞，金解放.2006.岩石声发射Kaiser点信号的小波分析及其应用初步研究［J］.岩石力学与工程学报，25（2）：3854－3858.

Coifman R R，Donoho D L.1994.Translation－invariant de－noising［M］∥Wavelets and Statistics.Springer Lecture Notes in Statistics 103.New York：Springer－Verlag：125－150.

Chang S G，Yu B，Vetterli M.2000.Adaptive wavelet thresholding for image denoising and compression［J］.IEEE Transation on Image Processing，9（9）：1532－1546.

Donoho D L，Johnstone I M.1994.Ideal sPatial adaptation via wavelet shrinkage［J］.Biometrika，81：425－455.

Mallat S，Hwang W L.1992.Singularity detection and processing with wavelet［J］.IEEE Transation on Information Theory，38（2）：617－643.

Johnstone L M，Silverman B W.1997.Wavelet threshold estimators for data with correlated noise［J］.J R Statist Soc，59（B）：319－351.

Zhang S，Salari E.2005.Image denoising using a neural network based non－linear filter in wavelet domain［J］.IEEE Transation on Image Processing，5（2）：989－992.

Xu Y，Weaver J，Healy M.1994.Wavelet transform domain filters：A sPatially selective noise filtration teehnique［J］.IEEE Transation on Image Processing，3（6）：747－758.

徐宏斌 现在华润置地（福州）有限公司工作.2011年厦门大学建筑与土木工程学院土木工程系岩土工程专业毕业，获工学硕士学位.曾主要从事声发射与微地震监测技术等方面的研究工作.

注：孟令媛、李宇彤、郑建常、蒋海昆、王秀英、宋美琴等的简介分别见本刊：Vol.33，No.4；Vol.30，No.4；Vol.29，No.4；Vol.17，No.4；Vol.31，No.6；Vol.33，No.5.

A study on method of signal denoising based on wavelet transform for micro－seismicity monitoring in large－scale rockmass structures

Xu Hongbin1）Li Shulin1），Chen Jijing2）
1）School of Architecture and Civil Engineering of Xiamen University，Fujan，Xiamen361005，China
2）Hunan Shizhuyuan Nonferrous Metals Company Limited，Hunan，Chenzhou423037，China

This paper applied wavelet denoising method to monitoring microseismicity in large－scale rockmass structure.The feasibility of using symlet6in wavelet denoising was validated with MATLAB simulation.Then four types of adaptive threshold rules for wavelet denoising are used to denoise three noisy signals.The result shows that the noise in signals can be filtered effectively with the four threshold rules and the Rigrsure threshold for wavelet denoising is more effective with the least mean square deviation and highest signal to noise ratio.Based on the multi－channel digital microseism monitoring system in Shizhuyuan mine，this paper applied wavelet denoising method to three different microseismic signals with the result of MATLAB simulation.The results show that the true microseismic signals can be recovered from the noisy signals by removing noise at every wavelet scale，even though noisy signals have low signal to noise ratio or include wide frequency range.The wavelet threshold denoising is suited especially to the denoising of microseismic monitoring signals in largescale rockmass structures.

wavelet de－noising；large－scale rockmass；microseismic technology；MATLAB simulation

10.3969／j.issn.0253－3782.2012.01.008

P315.9

A

徐宏斌，李庶林，陈际经.2012.基于小波变换的大尺度岩体结构微震监测信号去噪方法研究.地震学报，34（1）：85－96.

Xu Hongbin，Li Shulin，Chen Jijing.2012.A study on method of signal denoising based on wavelet transform for microseismicity monitoring in large－scale rockmass structures.Acta Seismologica Sinica，34（1）：85－96.

国家自然科学基金（10572122）资助.

2011－03－10收到初稿，2011－09－06决定采用修改稿.

e－mail：shulin.li＠163.com