基于改进卡尔曼滤波的RoboCup3D定位研究
杨 帆,王 浩
(1.黄山学院 国资处,安徽 黄山245021;2.合肥工业大学 计算机与信息学院,安徽 合肥230009)
1前 言
场上目标的定位是机器人基本技能之一。通过对目标的定位,才能使机器人清楚自己位置、目标位置和对手位置。[1,2]在此我们的球员主要是通过对标杆或目标的视觉信息来完成自身与目标的定位。[3]受限条件下视觉信息不能同时看到所有的标杆,我们需要考虑各种情况下的球员的自定位。
2 看不到标杆时自定位
通常看不到标杆的情形很少有,因为可以利用转头来获取标杆信息,但这种情形是可能的。此时可以使用正运动学计算确定自身位置。
机器人的定位技术可以分为两类,即相对定位和绝对定位。相对定位是根据机器人前一时刻的位姿和正运动学计算得出的。绝对定位是通过视觉信息得出。在此使用了相对定位的方法,相对定位由于会累计误差,时间越长精度越差,因此只能在比较短的路程精确定位。下面介绍具体使用方法。
机器人在正常情形中至少有一只脚着地(这里暂不考虑倒下情形),将上一周期计算出的机器人的坐标的x、y当成陀螺仪的x、y坐标分别计算两只脚的中心的坐标(此时脚的z值为0),以着地脚为起点使用正运动学计算到本周期的陀螺仪的向量,上一个周期的着地脚的坐标加上此向量便是本周期的陀螺仪坐标。这里没使用摄像头是因为陀螺仪与摄像头的x、y坐标几乎一样,而且减少了很多计算。机器人各腿部关节的滚动角(roll),俯仰角(pitch),偏摆角(yaw),由机器人运动学知其旋转矩阵。

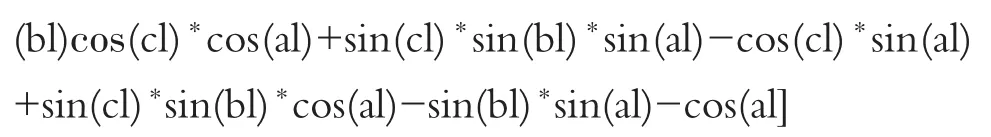
由链乘法则可求其各关节的位姿,这就完成了相对定位,实验效果如图1所示。

图1 看不到标杆情形下的相对定位
从图1可以看出,刚开始是误差还比较小,随着时间的推移,积累的误差将越来越大,这种方法适合于紧急情况下的短时定位,此时还未考虑智能体倒下情形,不适用长时间定位。
3 看到一个标杆时自定位
这里便是要完成相对定位和绝对定位的结合。此时的相对定位是利用上一周期的面向角和陀螺仪的角速度来计算本周期的面向角。
本周期的面向角等于上一周期的面向角加前3个周期的陀螺仪的角速度分别乘0.02再相加。然后利用公式 (x,y,z)=(d*cosφ*cosθ,d*cosφ*sinθ,d*sinφ),d、θ、φ分别表示 t时刻球员或球与所选标志杆之间的距离、水平方向的角度和垂直方向的角度。是将人的面向角加上头的转角再加上视觉信息中的水平偏角。
接着用公式进行计算:P=PF-P',其中PF为标志的坐标,P'是由极坐标转化后的直角坐标。但是这种方法无法处理误差所带来的干扰,实验效果如图2所示。
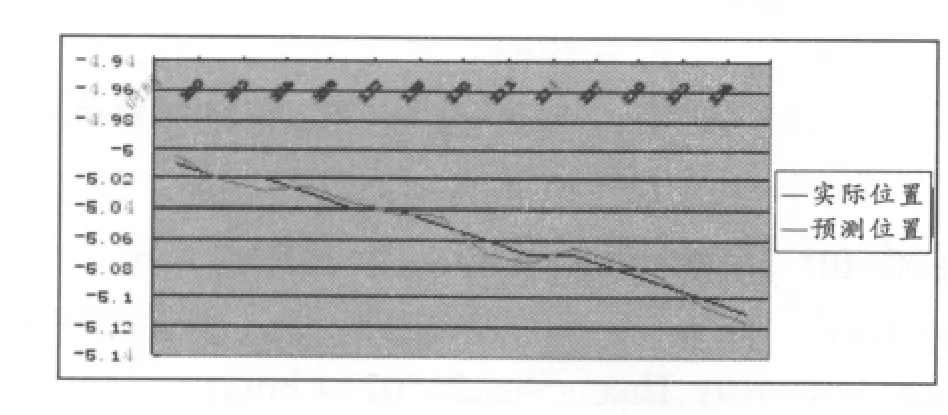
图2 看到一个标杆的情形下的自定位
从图2可以看出,在短时定位其精度不如无标杆的情形,但不会随着时间的推移产生积累误差。这便孕育出想将两种方法结合的想法,事实上是可以实现的。
4 看到多个标杆时自定位
多个标杆的自定位方法较多,但都存在着误差。最容易想的是每个标杆都计算后取平均。若是两个标杆可结合自身高度和到标杆的距离来计算(角度的偏差较大一般不采用角度),因为在一个平面上到空间两点的距离可以唯一地确定一点(两点的连线不垂直于此面)。
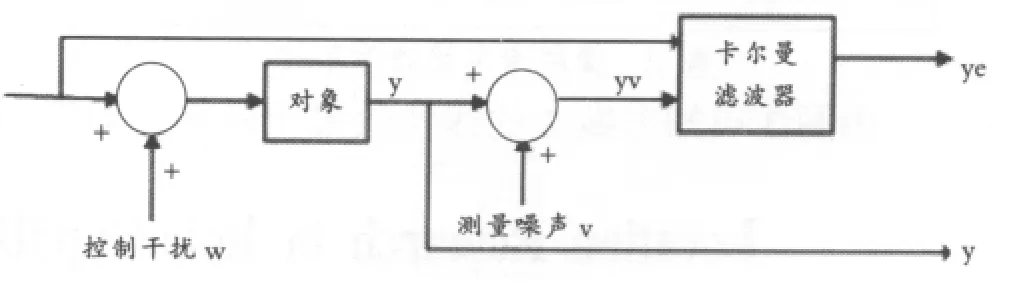
国际比赛中视觉噪声的设置是与距离有关,距离、水平角和高度角误差均是以0为期望的正态分布,标准差分别为0.0965,0.1225和0.1480。实测结果是误差标准差近似为距离的线性函数。对于随机线性系统,当模型准确且系统过程噪声和观测噪声为高斯白噪声序列,方差已知时,卡尔曼滤波有近似完美的效果。因此我们选用卡尔曼滤波的方法来减小误差。
卡尔曼滤波是一种最优化自回归数据处理的算法。可以理解成是相对定位和绝对定位的信息中更相信谁相信多少的一种算法。这将引出一个概念卡尔曼增益K,可理解为K和上周期的最优解里储存了应回归的数据。而K是通过协方差来进行更新的。相对定位即预测值我们有两种方案:
1.无标杆下的定位使用的方法即正运动学的计算。
2.是利用陀螺仪的相关信息来计算。
在距离上利用ACC中上周期的加速度和计算出的速度来计算本周到标杆的距离。St=S0+(v*t+0.5*a*t*t)*,a为加速度在人与标杆连线上的分加速度,θ为面向与人与标杆连线的夹角。水平方向的角度的相对定位与一个标杆的情形下的自定位一样。方案1的计算量较大,但比较准确。方案2的计算量较小,由于假设模拟了控制量,便有过程误差,降低的准确度。卡尔曼滤波的流程为:
1.预估计:X(k)^=F(k,k-1)·X(k-1)
2.计算预估计协方差矩阵:
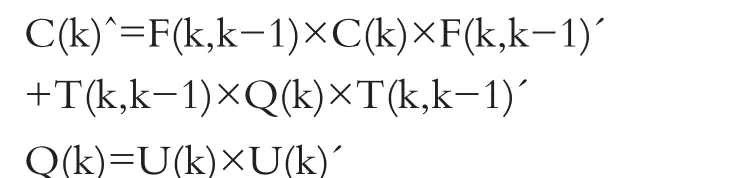
3.计算卡尔曼增益矩阵:
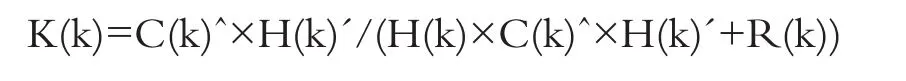
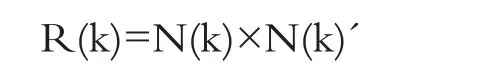
5.计算更新后估计协方差矩阵:
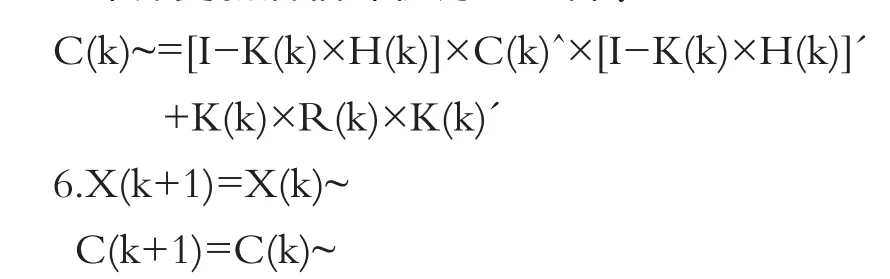
在使用卡尔曼滤波时也有两种算法:
1.使用含8个元素的数组,这样避免各个标杆有干扰,每个元素分别使用卡尔曼滤波,每3个周期更新一次。得到经滤波后的视觉信息后在计算定位。此方案在能看到两个或以上的标杆时不需角度便能定位,角度标准差较大,避免使用了角度。其协方差为0.00931225。可直接代入使用,不用考虑转移矩阵和过程噪音。
2.首先利用最近标杆的视觉信息作观测值和上个周期的预测(相对定位的方法)来得到一个最优解。再用最优解作预测值,和较远的标杆视觉信息再使用卡尔曼滤波,这样可以大大的提高精确度。只是这样K会很相信预测值,如在机器人倒下后回归速度会慢些。所以在爬起时的几个周期内不要使用滤波。若是使用正运动学的计算来预测值可令状态转移矩阵为E,预测使用的是直角坐标在预测后应将其化为极坐标,在计算最优解和协方差的更新时都使用极坐标,距离、水平角和高度角的标准差在直角坐标中不能直接用,如图3所示。

图3 使用卡尔曼滤波定位
由图3可知方案2的线性效果比较好。同时,在实际应用中发现,机器人虽然能够很好地定位,但是花费时间较长,停顿时间较长,我们试着把算法中的卡尔曼增益K值经过实验后得到一个近似值,用近似值取代算法的第3步中的更新计算,这样算法得到了优化,定位速度明显加快,误差略微增加,此时需要兼顾定位准确和定位速度这两个方面,后期可以继续使用几何地图和概率推理的定位方法等,不断提高定位准确度。
5 总结与展望
虽然移动机器人定位问题已经研究多年,但是现有的各种方法都仍然存在种种不足,在解决定位问题中遇到的不确定性问题上各种方法各有优缺点。当前移动机器人的研究非常强调自主能力的提高,定位系统越来越重视算法的鲁棒性、主动性和安全性,研究重点从局部、静态、被动的方式向全局、动态、主动定位方法发展,并且强调不能孤立地设计定位系统,主张将路径规划、避障控制、地图构造、对象识别等都集成到定位系统中,控制结构及位姿估计算法越来越复杂,其中一些快速、精确的定位算法均以激光雷达数据为基础。
[1]孙海梦.基于视觉噪声的粒子滤波定位法在RoboCup中的应用[J].计算机工程与科学,2008,30(12):41-42.
[2]陈思,易益敏,等.RoboCup3D基于αβγ滤波的足球定位方法[C].2009年中国智能自动化会议,2009.
[3]方正,佟国峰,等.基于贝叶斯滤波理论的自主机器人自定位方法研究[J].控制与决策,2006,(08):841-847.

