一类出现在燃烧理论中的奇摄动边值问题
方晓玲 ,周 健 ,刘树德
(1.安徽大学 数学科学学院,安徽 合肥230601;2.安徽师范大学 数学系,安徽 芜湖 241000)
1 引 言
奇异摄动理论和方法是当前解决工程技术和科学问题的主要数学工具之一,在天体力学、流体力学、量子力学、弹性力学、化学反应理论、燃烧理论、光的传播和非线性振动等学科得到了广泛的应用,[1-7]例如 Willams,[1]章国华和 Howes[4]讨论了几类出现在燃烧理论中的奇摄动Dirichlet问题。
本文在此基础上考虑如下形式的奇摄动Robin问题
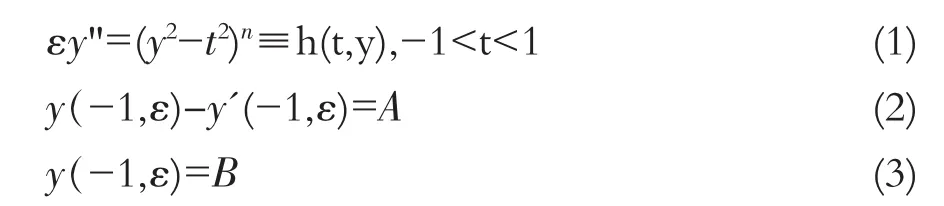
其中y为燃烧火焰的密度,ε为反应速度的扩散率,它是一个正的小参数,t为燃烧位置,A≥2和B≥1为常数,n≥1为正整数。
我们通过选取适当的具有边界层性质和角层性质的函数构造出一对界定函数,应用微分不等式理论证明问题(1)-(3)存在具有角层性质的解,并给出解的渐近估计,为此需要用到如下引理。
引理[4]: 考虑二阶非线性常微分方程Robin问题)))

其中函数 f在区域 D=[a,b]×R2中连续, f(t,y,z)=O (|z|2) ((|z|) →+∞)。 p,q 是 非 负 常 数且不同时为零。 假设存在函数 α(t),β(t)∈C2[a,b]使得
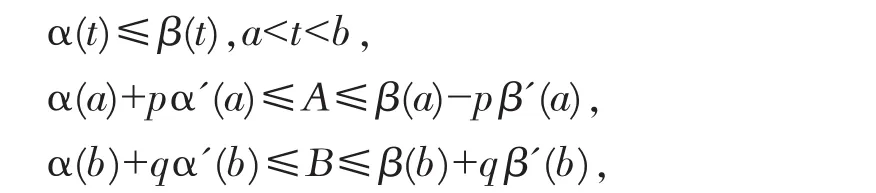
及微分不等式
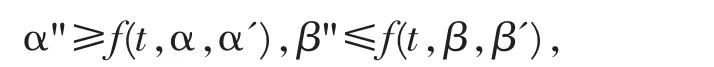
则问题(4)-(6)在区间[a,b]上存在一个解 y=y(t),并成立不等式
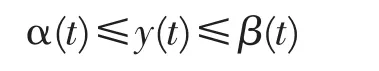
α(t),β(t)通常称为问题(4)-(6)的一对界定函数。1968年Jackson[8]减弱了对界定函数的要求:若在[a,b]上存在分划{t}:a=t0<t1<…<tn=b,使得 α,β∈C2[ti-1,ti](i=1,2,…,n)(在左、右端点处的导数分别指右导数和左导数),即 α(t),β(t)为[a,b]上分段 C2类函数,且在
其中K2为确定的常数。当t0=0时,(10)写为
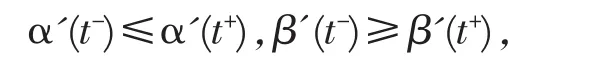
及
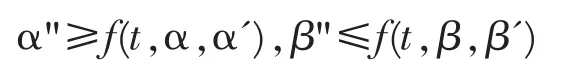
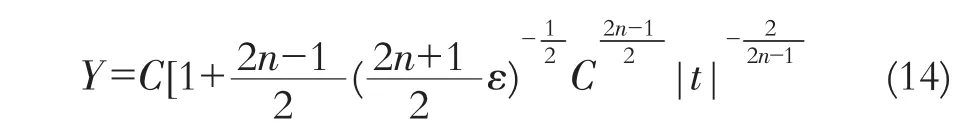
则引理的结论仍成立。
2 构造具有边界层和角层性质的函数
由于退化解u(t)=|t|的导数在t=0处有跃度u'(0+)-u'(0-)=2,需要在t=0处构造具有角层性质的函数。在(14)中令
当反应率ε=0时,问题(1)-(3)退化方程

可得

于是
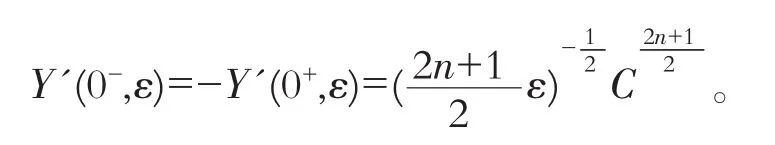
从而得到
有解 u1=-t和 u2=t。选取方程(7)在[-1,1]上的一个稳定解 u(t)=|t|。
助方程
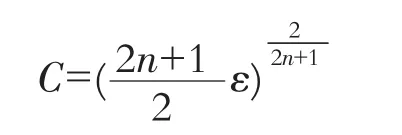
方程(8)在I上具有如下形式的代数型渐近角层解


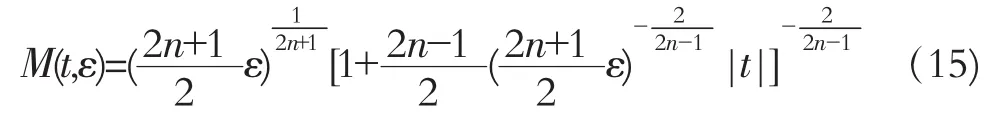
其中C为任意常数,λ,μ是与t0有关的常数。将(9)代入(8)得
它是一个在t=0处具有角层性质的函数。
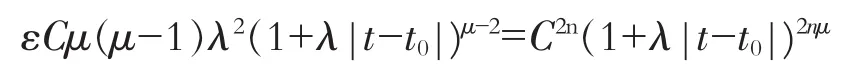
从而得出
3 解的存在性及解的渐近估计
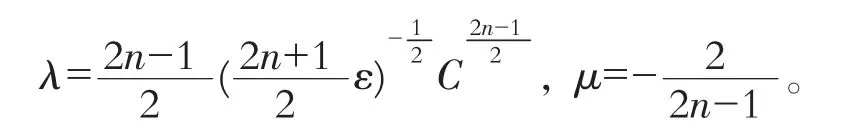
于是

应用微分不等式理论,我们来证明解的存在性,并给出解的渐近估计。
定理:设 A≥2,B≥1,则燃烧问题(1)-(3)在[-1,1]上存在一个解y(t,ε)具有如下形式的渐近估计式:
当 t0=-1 时,(10)写为
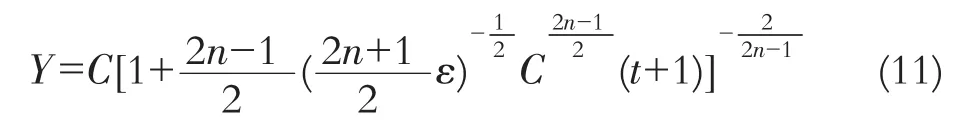
注意到问题(1)-(3)的解与(7)的稳定解u(t)=|t|在

令
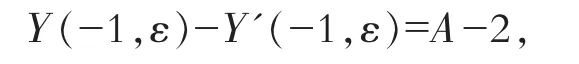

由(11)得
其中 0<ε<<1,n≥1 为正整数。
证明:构造界定函数 α(t,ε)和 β(t,ε)如下



其中 L(t,ε),R(t,ε)和 M(t,ε)分别由(12),(13)和(15)确定,r为待定的正常数。由(17)可知

且容易推出
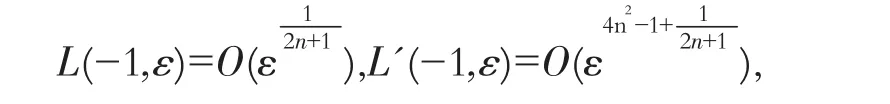

于是

选择 r≥σ,便有

同理可得

接着我们证明在 t∈(-1,0)∪(0.1)上

事实上,由于
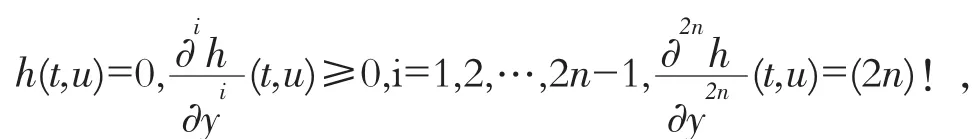
可得

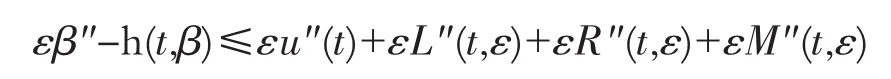
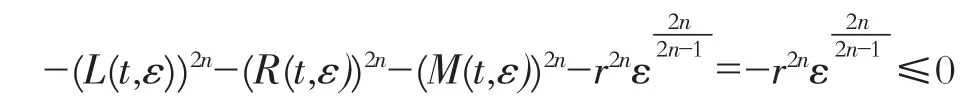
即(22)成立。
注意到函数 α(t,ε)和 β(t,ε)在 t=0 不可导,但显然成立
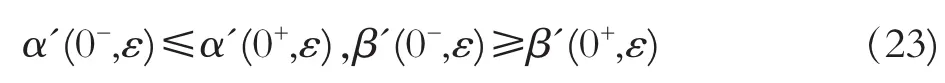
根据引理及Jackson[8]推广的微分不等式理论,从(18)-(23)推出,对充分小的正数 ε,问题(1)-(3)在[-1,1]上存在一个解 y(t,ε),并满足不等式
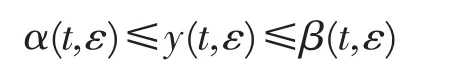
因此渐近估计式(16)成立,定理证毕。
[1]Willams,F.A.Theory of combustion in laminar flows[J].Ann Rev Fluid Mech,1971,3:171-188.
[2]江涛,刘树德.一类出现在化学反应器理论中的奇摄动边值问题[J].黄山学院学报,2011,13(5):13-15.
[3]Nayfeh,H,Introduction for Perturbation Techniques[M].New York:John Wiley&Sons,1981:394-432.
[4]Chang K.W,and Howes F.A Nonlinear Singular Perturbation Problems:Theory and Applications[M].New York:Spring Verlag,1984:153-208.
[5]林宗池,周明儒.应用数学中的摄动方法[M].南京:江苏教育出版社,1995:123-126.
[6]de Jager,E.M.and Jiang Furu,The Theoy of Singular Perturbations[M].Amsterdam:Elsvier.1996:276-291.
[7]刘树德,鲁世平,姚静荪,等.奇异摄动边界层和内层理论[M].北京:科学出版社,2012:124-151.
[8]Jackson,L K,Subfunctions and Second-Order Ordinary Differential Inequalities[J].Adv in Math,1968,(2):307-363.

