基于热刺激电流的空间电介质载流子迁移率测量方法

李盛涛，李巍巍，闵道敏，林 敏，黄 印

(西安交通大学电力设备电气绝缘国家重点实验室，陕西西安710049)

1 引言

空间环境中的高能电子可以穿透航天器表面覆层进入空间介质内部。当电子沉积速率大于介质内电荷泄漏速率时，介质中会沉积空间电荷，介质内电场会严重畸变。当电场较高时会引发放电现象，影响航天器内电子系统的可靠性;当该电场超过介质的临界场强时，就会发生空间介质击穿，导致航天器运行故障，甚至使整个航天器失效［1］。适当地提高空间材料在空间环境下的迁移速率可以提高介质内部电荷的泄漏速度，在一定程度上缓解充放电问题［2～4］。因此，通过提高测量介质电荷迁移率的精确度，深入研究空间介质电荷输运机理可以为缓解航天器介质深层充放电问题提供必要的理论和实验基础，为空间材料的改性及新材料的引入提供必要的理论支撑，对保证航天器高效安全运行具有重要意义。

目前国内外测量有机聚合物载流子迁移率的方法主要有渡越时间法、空间电荷限制电流法、场效应管法、脉冲辐照实时微波电导技术等［5，6］。上述方法多适用于无机半导体材料迁移率的测量，而空间聚合物材料的载流子迁移率低，且变化范围大，用以上方法很难得出满意的测量数据。有机高聚物中载流子迁移率的测量技术仍处于初级阶段，还不能精确测量空间介质迁移率，要确定聚合物的载流子迁移率仍需要做很多工作［7，8］。

热刺激电流(TSC)是研究材料电导特性和介电特性的一种快速有效的方法。用这种方法不仅可以观测荷电粒子从低温不平衡状态经升温到高温热平衡状态全过程中的变化，而且还可以得出荷电粒子的活化能、陷阱能级、松弛时间等参数［9～11］。

本研究在热刺激电流的基础上，引入玻尔兹曼分布函数，提出了基于热刺激电流的载流子迁移测量模型。根据实验结果，计算得出了典型空间有机介质的迁移率。

2 实验

2.1 试样制备

聚酰亚胺(PI)具有耐辐射、耐高低温、机械性能好、介电性能优良等突出优点，被广泛用于航空、航天高技术领域［12］。本研究选用PI薄膜来研究空间介质的导电率测量方法及导电机理。将厚度为0.05 mm的聚酰亚胺薄膜剪成边长为2.5 cm的方形，在超声波仪中，分别用去离子水、乙醇清洗3次，每次5 min，再将清洗过的试样置于烘箱内烘干，以消除试样中水分、表面污秽、空间电荷等因素的影响。采用离子溅射仪对试样溅射直径为2 cm的双金电极系统，并用万用表确认导通。

2.2 实验设备

实验主要采用TSC测量系统，利用该系统的温度控制装置对试样进行连续升温，把测量的温度范围从低温区扩展到高温区，同时对薄膜试样施加较高电压;利用SBC-12型离子溅射仪对试样进行喷金处理;静电计6517A测量空间电荷限制电流;利用Delta温箱和ZC36型高阻计辅助测量不同温度下空间电荷限制电流。

2.3 基于热刺激电流的载流子迁移测量模型

基于TSC的载流子迁移率模型是在热刺激电流原理的基础上引入玻尔兹曼分布函数，利用所得到的TSC测量数据求解载流子迁移率。这种方法避免了原理上的繁琐复杂的推导，通过假定的玻尔兹曼分布即可算出陷阱电荷与自由电荷数目，方便了计算机(MATLAB)的模拟计算。基于TSC的迁移率测量原理图如图1所示。

假定电荷由阴极注入并被介质内陷阱捕获沉积在介质表面0～δ区间内;短路时，0～δ区间内所捕获的电荷全部传导到电极［10，11］。则由0～δ区间激发的自由电子迁移在外电路表现的电流I为:

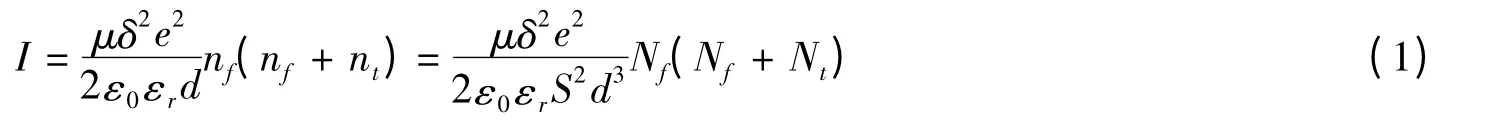
式中 nf为自由电荷浓度;nt为陷阱电荷浓度;Nf为自由电荷总数;Nt为陷阱电荷总数;S为试样的表面积;e为电子电量;ε0为真空中的介电常数;εr为介质相对介电常数。Nf一般比Nt小很多，可将式(1)简化为

得到载流子迁移率为

Webar等经过研究给出一些经验公式来近似描述高能电子在介质材料中的沉积［1］，能量为E的电子的最大射程δ为

高能电子在介质材料一定的深度呈统计分布，假设电荷的能量服从玻尔兹曼分布

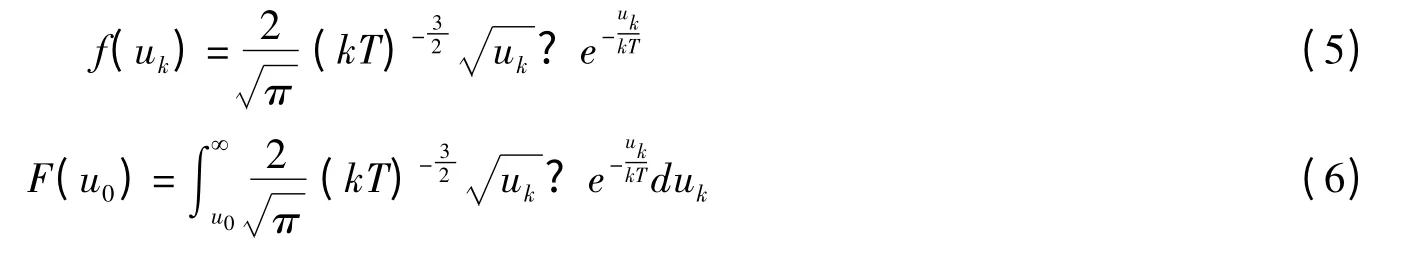
式中 uk为载流子的能量;u0为活化能。则温度为T时自由电荷总数为

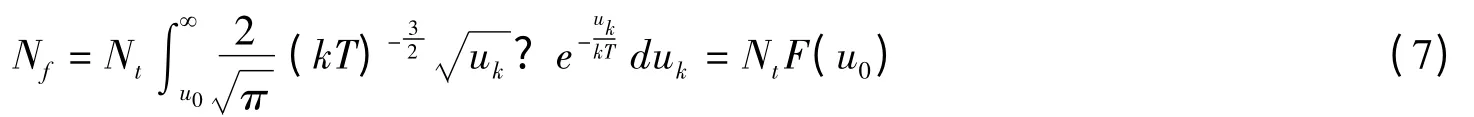
TSC 升温公式为［10，11］

式中 T0为初始升温的温度;β为升温速率;t为升温时间。则起始的Nt1可以由式(8)和电荷量公式得到

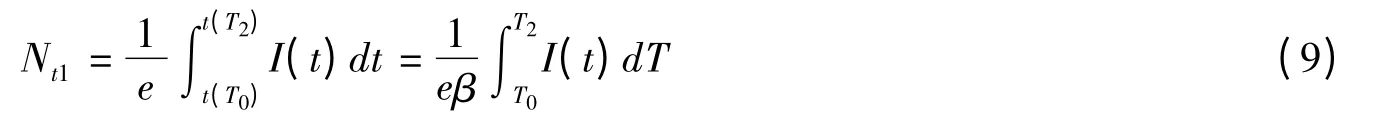
存在递归关系

式中 Nfn温度为Tn时自由电荷总数;Ntn温度为Tn时陷阱电荷总数;Fn表示温度为Tn时玻尔兹曼分布函数。因此可以利用TSC曲线，通过MATLAB仿真计算，得到Nf、Nt、μ与温度的关系。

2.4 基于空间电荷限制电流的载流子迁移测量模型

忽略介质中陷阱对电子的捕获作用，空间电荷所引起的电流包括漂移电流和扩散电流两部分［13］。

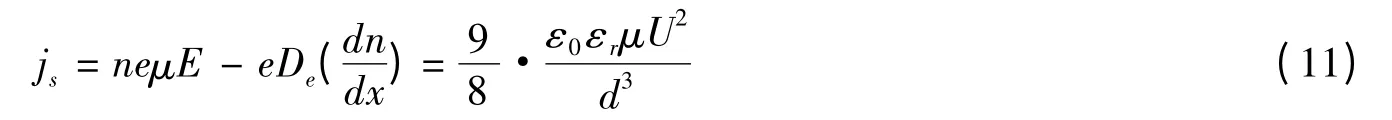
式中 n为空间电荷体积浓度;De为电子的扩散系数。

考虑到陷阱电荷的作用，得到［14］

通过TSC曲线求解nf/(nf+nt)，对实验得到的数据进行校正。

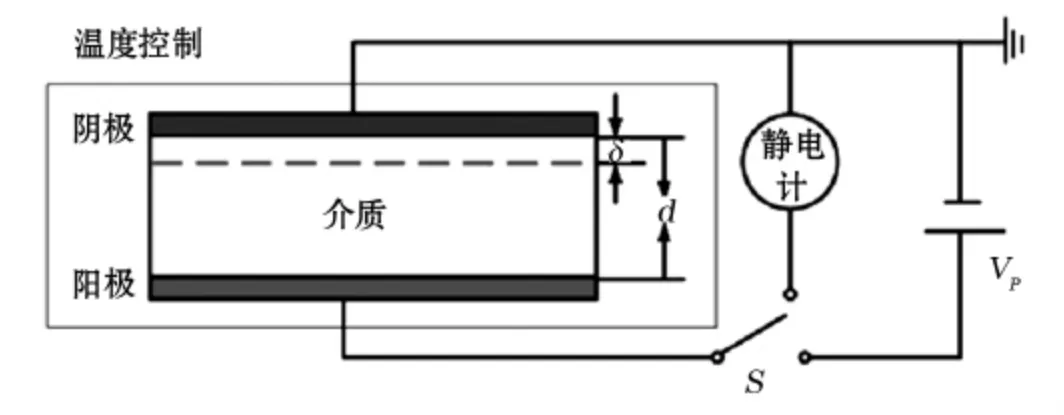
图1 基于TSC的迁移率测量电路原理图

3 结果与讨论

图2为PI薄膜热刺激电流测试结果及活化能计算结果。在实验温度范围内发现PI薄膜的热刺激电流仅存在一个峰，TSC峰值出现在440 K左右，它与Tanaka在173℃发现的TSC的α峰及王惠明［15］在160℃附近发现的唯一的TSC峰类似。实验中测得的TSC结果为聚酰亚胺薄膜热刺激去极化电流，是由冻结在陷阱中的电极注入电子在升温过程中热激发逸出陷阱形成的电流。可以推测PI薄膜热刺激电流峰是由介质材料内部陷阱俘获电极注入的电子造成的。基于TSC测试结果，根据热刺激电流起始上升法计算出PI薄膜的活化能为H=0.356 eV，如图2所示。

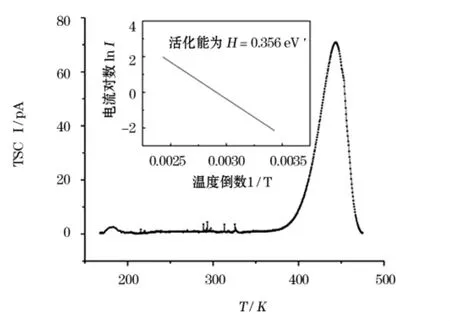
图2 PI薄膜的热刺激电流与温度关系

利用MATLAB对试样TSC测试数据进行仿真计算，结果如图3所示。图3(a)(b)分别表示剩余电荷及自由电荷与温度的关系，(c)(d)则表示载流子迁移率与温度的关系。可知，介质中陷阱电荷总数Nt随温度升高而减少;自由电荷Nf的计算曲线与实际相符，体现了空间介质电荷输运过程。从图3(c)(d)可以看出，温度位于300～400 K时，载流子迁移率随着温度的升高而呈指数方式增长。由图3(d)可知，从室温(300 K)到高温区(400 K)，空间电荷限制电流方法测量的PI薄膜的载流子迁移率在10－16m2/V·s到10－13m2/V·s范围内;由TSC曲线求得的PI薄膜的载流子迁移率在10－13m2/V·s到10－10m2/V·s范围内;引入基于TSC曲线求解的修正比例系数之后，利用改进空间电荷限制电流方法得到的PI薄膜的载流子迁移率从10－12m2/V·s到10－10m2/V·s范围内，载流子迁移率值比未修正之前大3～4个数量级，比由TSC曲线求得的大一个数量级左右。聚合物材料属于非晶态有机材料，迁移率较低，多为10－12～10－5m2/V·s。基于TSC的载流子迁移率测量模型得到的结果与改进空间电荷限制电流方法测得的结果接近，并位于这个量级范围内。

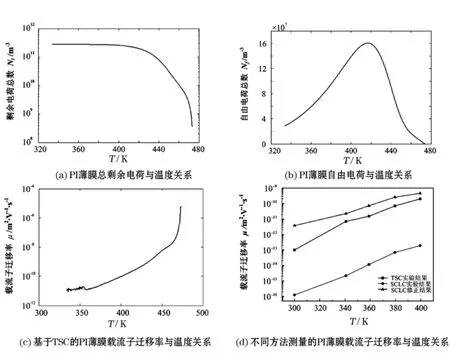
图3 基于TSC的PI薄膜载流子迁移率计算

4 结论

本研究提出的基于TSC的载流子迁移率测量模型是一种新的测量聚合物载流子迁移率的方法，能够比较精确地得到强场下较大温度范围内的载流子迁移率。该模型研究分析得聚酰亚胺薄膜的热刺激电流峰是由介质内部陷阱俘获电极注入的电子所致。该研究为空间介质电荷输运机理的研究及空间材料改性提供了基础。

［1］闫小娟.卫星介质充电机理和实验研究［D］.北京:中国科学院研究生院，2008.

［2］MULVILLE D R，et al.Avoiding Problems Caused by Spacecraft On-Orbit Internal Charging Effects［R］，NASA-HDBK-4002，1999.

［3］PURVIS C K，GARRETT H B，WHITTLESEY A C，et al.Design Guidelines for Assessing and Controlling Spacecraft Charging Effects［R］.NASA TP-2361，1984.

［4］GARRETT H B，WHITTLESEY A C.Spacecraft Charging，An Update［J］.IEEE Transactions on Nuclear Science，2000，28:2017～2028.

［5］SANJAY TIWARI，GREENHAM N C.Charge mobility measurement techniques in organic semiconductors［J］.Opt Quant Electron，2009，41:69～89.

［6］文尚胜，彭俊彪，曹镛.渡越时间方法测量聚合物材料的载流子迁移率［J］.激光技术，2005，29(3):301～303.

［7］DENNISON J R，BRUNSON J，SWAMINATHAN P，et al.Methods for high resistivity measurements related to spacecraft charging［J］.IEEE Transactions on Plasma Science，2006，34:2191 ～2203.

［8］FREDERICKSON A R，DENNISON J R.Measurement of conductivity and charge storage in insulators related to spacecraft charging［J］.IEEE Transactions on Nuclear Science，2003，50:2284 ～2291.

［9］FLEMING R J.Thermally—Stimulated Conductivity and Luminescence in Organic Polymers［J］.IEEE Transactions on Electrical Insulation，1989，24(3):523～531.

［10］王力衡.介质的热刺激理论及其应用［M］.北京:科学出版社，1988.

［11］杨春.TSC测量装置的改进及聚酰亚胺薄膜TSC的测量［D］.哈尔滨:哈尔滨理工大学，2007.

［12］祝力伟，赵慨，邱家稳，等.新型热控涂层Al-Al2O3金属陶瓷复合膜制备与性能研究［J］.真空与低温，2008，14(4):219～222.

［13］陈季丹，刘子玉.电介质物理学［M］.北京;机械工业出版社，1982.

［14］MURGATROYD P N.Theory of space-charge-limited current enhanced by Frenkel effect［J］.Journal of Physics D:Applied Physics，1970，3:151～156.

［15］王惠明，FOURACRE R A，TEDFORD D J.高场强下聚酰亚胺薄膜电导的研究［J］.西安交通大学学报，1991，25(6):73～78.